Understanding the basics of Blockchain: The challenge of the Byzantine Generals. Part 1
The translation of the article was prepared especially for students of the course “High Load Architect” , which starts this month.

Blockchain is a decentralized system consisting of various entities that act depending on their incentives and the information they have.
Whenever a new transaction is broadcast over the network, nodes can include this transaction in a copy of their ledger or ignore it. When most network participants decide to accept a certain state, consensus is reached.
A fundamental problem in distributed computing and multi-agent systems is to achieve overall system reliability in the presence of a number of inoperative processes. Often this requires that the processes coordinate among themselves some value that will be needed during the calculation.
These processes are described as consensus.
For a consensus protocol to be secure, it must be fault tolerant.
To begin with, we will briefly talk about the insoluble problem of two generals. Then, consider the Byzantine Generals Problem and discuss Byzantine fault tolerance in distributed and decentralized systems. And at the very end, let's talk about how this all relates to blockchain technology.
This task, first published in 1975 and named in 1978, describes a scenario in which two generals attack a common enemy. The first general is considered the leader, and the second is the follower. The army of each general individually is not enough to defeat the enemy army, so they need to cooperate and attack at the same time. This scenario looks simple, but there is one caveat:
In order for them to communicate and agree on a time, the first general must send a messenger through the enemy’s camp, he must deliver a message with the time of the start of the attack to the second general. However, there is a possibility that the messenger will be captured by opponents, and the message will not be delivered. This will lead to the fact that the army of the first general will go on the attack, and the second will remain in place.
Even if the first message is delivered, the second general must acknowledge (ACK (acknowledge), note the similarity to the three-way handshake in TCP ) that he received the message, so he sends the messenger back, thereby reproducing the previous scenario where the messenger can be captured . This flows into endless ACKs, and because of this, the generals cannot reach agreement.
There is no way to guarantee the second condition, that is, that each general is fully confident that the other agrees to the plan of attack. Both generals will always be ignorant of whether the messenger has reached his comrade.
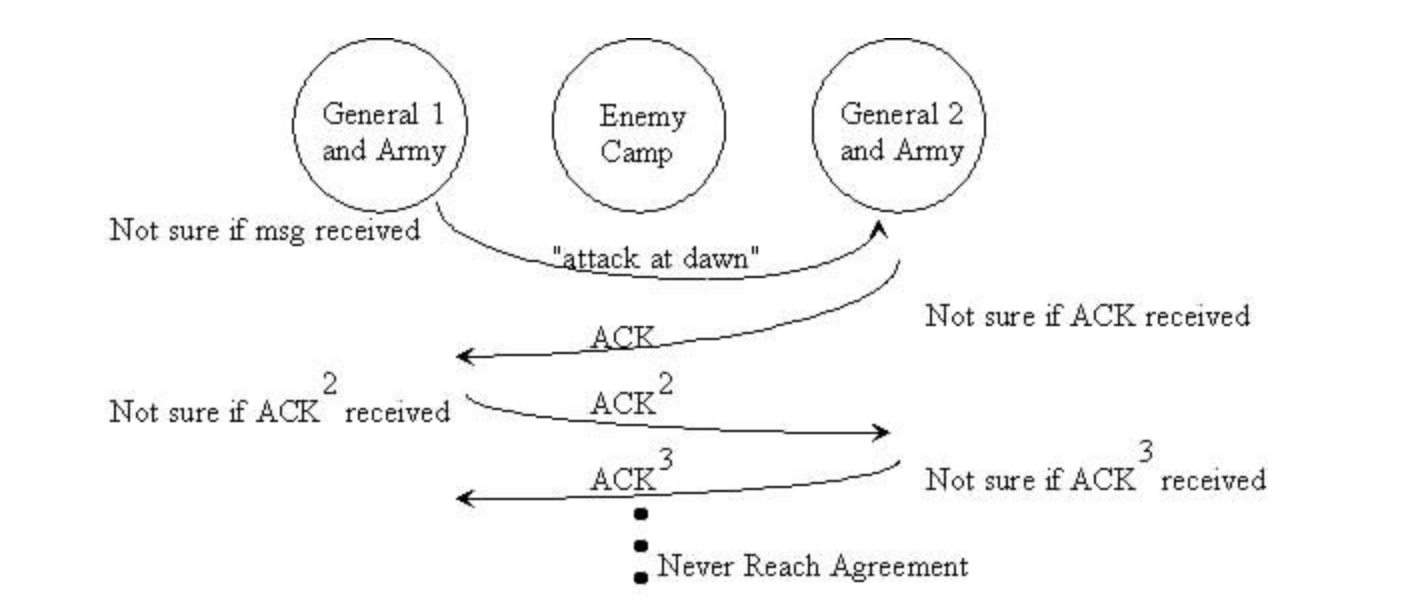
It was proved that the task of two generals is unsolvable.
Described in 1982 by Lamport, Shostak and Piz, the version of this problem turned out to be a highlight. She describes the same scenario where, instead of two generals, a larger number of generals should agree on an attack time. An additional complication is that one or more generals can be traitors, that is, they can lie about their intentions (for example, the general says that he agrees to attack at 09:00, but does not).
The paradigm of the leader-follower, described in the task of two generals, is transformed into a commander-subordinate installation. To achieve consensus here, the commander and each subordinate must agree on the same solution (attack or retreat).

In addition to the second point, an interesting fact must be pointed out: if the commander is a traitor, then consensus must still be reached. As a result, all lieutenants have a majority vote.
The consensus algorithm in this case is based on the meaning of most decisions that subordinates see.
Theorem: For any m , the OM (m) algorithm reaches a consensus with more than 3m generals and a maximum of m traitors.
This means that the algorithm can reach consensus while 2/3 of the participants are honest. If the traitors are more than 1/3, consensus is not reached, the armies cannot coordinate their attacks, and the enemy wins.
OM algorithm (0)
OM algorithm (m), m> 0
When m = 0 there are no traitors, each subordinate follows the order. For m> 0, each final choice of a subordinate proceeds from the predominant part of the election of all subordinates.
It will be clearer if you look at the situation from the point of view of the second subordinate - let C be the Commander, and L {i} is the i-th subordinate.

OM (1): Subordinate 3 is a traitor. The situation from the point of view of the second subordinate.
Steps:
The final decision is made from a majority of the votes of L1, L2 and L3 and as a result consensus is reached.
It is important to remember that the goal is for most subordinates to choose the same solution, rather than a specific one.
Let's look at the case when the commander is a traitor.
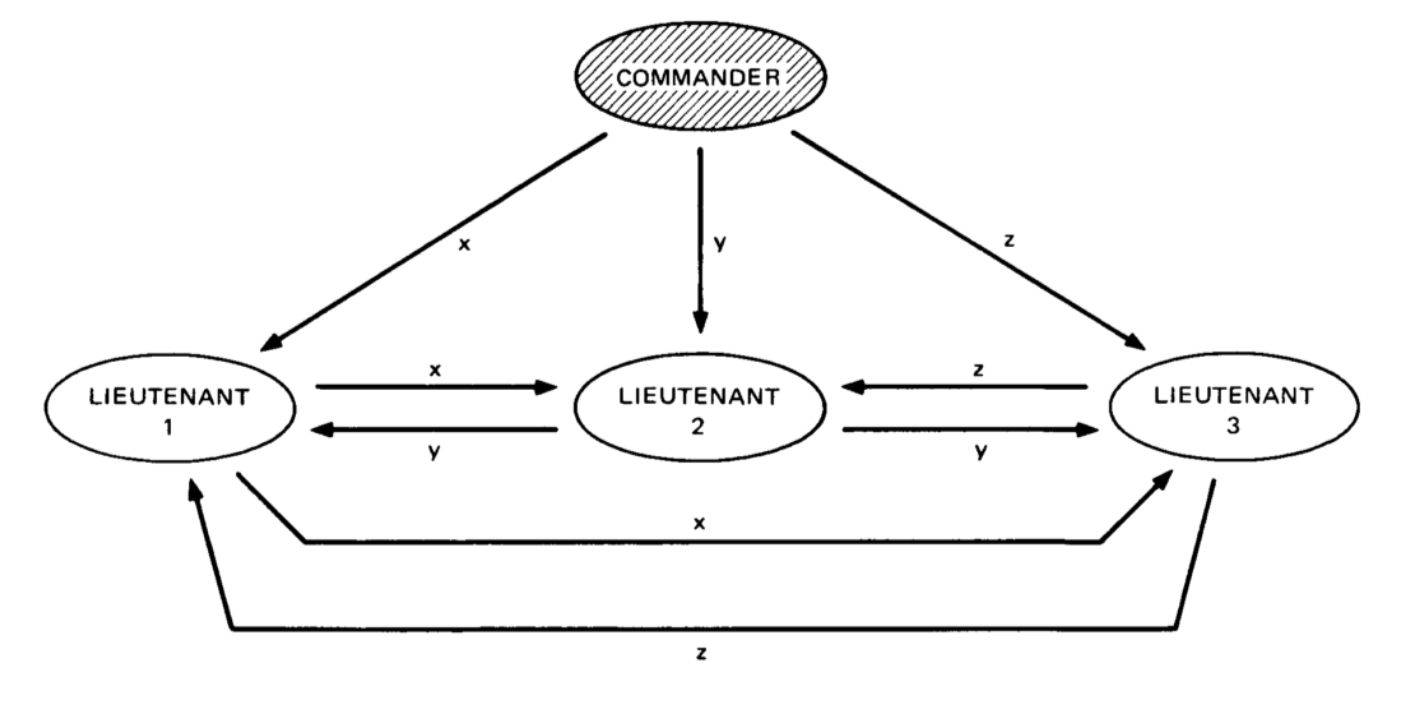
OM (1): The commander is a traitor.
Steps:
They all have the same value, so consensus is reached. Note that even if the values of x, y, z are all different, the majority value (x, y, z) is the same for all three subordinates. If x, y, z are completely different orders, we can assume that they will act according to the default plan - RESET.
To look at a practical approach to a more complex example with 7 generals and 3 traitors, I suggest you read this article .
Byzantine fault tolerance is a characteristic that defines a system that allows for a failure class that belongs to the Byzantine Generals Task. Byzantine failure is the most complex class of failure modes . It does not imply any restrictions and makes no assumptions about what kind of behavior a node can have (for example, a node can generate any arbitrary data, posing as an honest participant).
Byzantine mistakes are the hardest to fix. Byzantine fault tolerance was necessary in aircraft engine systems, in nuclear power plants, and in virtually any system whose actions depend on the results of a large number of sensors. Even SpaceX sees it as a potential requirement for its systems.
The algorithm mentioned in the previous section corresponds to Byzantine fault tolerance until the number of traitors exceeds one third of all generals. There are other options to facilitate this task, including the use of digital signatures or the introduction of restrictions on communication between peers.
Blockchain are decentralized ledgers that, by definition, are not controlled by the central authority. Due to the values stored in them, attackers have a good economic incentive to try to initiate a mistake. Nevertheless, the Byzantine fault tolerance and, therefore, the solution of the Byzantine generals problem for the blockchain are simply necessary.
In the absence of Byzantine Fault Tolerance, a peer can transmit and publish false transactions, completely nullifying the reliability of the blockchain. To make matters worse, there is no central authority that can take responsibility and repair damage.
When Bitcoin was invented, the big breakthrough was the use of evidence of the probabilistic solution of the Byzantine Generals problem. It was described in detail by Satoshi Nakamoto in this email .
In this article, we examined some basic concepts of consensus in distributed systems.

Blockchain is a decentralized system consisting of various entities that act depending on their incentives and the information they have.
Whenever a new transaction is broadcast over the network, nodes can include this transaction in a copy of their ledger or ignore it. When most network participants decide to accept a certain state, consensus is reached.
A fundamental problem in distributed computing and multi-agent systems is to achieve overall system reliability in the presence of a number of inoperative processes. Often this requires that the processes coordinate among themselves some value that will be needed during the calculation.
These processes are described as consensus.
- What happens when a participant decides not to follow the rules and intervene in the state of his ledger?
- What happens when there are a lot of such participants in the network, but not the majority?
For a consensus protocol to be secure, it must be fault tolerant.
To begin with, we will briefly talk about the insoluble problem of two generals. Then, consider the Byzantine Generals Problem and discuss Byzantine fault tolerance in distributed and decentralized systems. And at the very end, let's talk about how this all relates to blockchain technology.
The task of two generals
This task, first published in 1975 and named in 1978, describes a scenario in which two generals attack a common enemy. The first general is considered the leader, and the second is the follower. The army of each general individually is not enough to defeat the enemy army, so they need to cooperate and attack at the same time. This scenario looks simple, but there is one caveat:
In order for them to communicate and agree on a time, the first general must send a messenger through the enemy’s camp, he must deliver a message with the time of the start of the attack to the second general. However, there is a possibility that the messenger will be captured by opponents, and the message will not be delivered. This will lead to the fact that the army of the first general will go on the attack, and the second will remain in place.
Even if the first message is delivered, the second general must acknowledge (ACK (acknowledge), note the similarity to the three-way handshake in TCP ) that he received the message, so he sends the messenger back, thereby reproducing the previous scenario where the messenger can be captured . This flows into endless ACKs, and because of this, the generals cannot reach agreement.
There is no way to guarantee the second condition, that is, that each general is fully confident that the other agrees to the plan of attack. Both generals will always be ignorant of whether the messenger has reached his comrade.

It was proved that the task of two generals is unsolvable.
The task of the Byzantine Generals
Described in 1982 by Lamport, Shostak and Piz, the version of this problem turned out to be a highlight. She describes the same scenario where, instead of two generals, a larger number of generals should agree on an attack time. An additional complication is that one or more generals can be traitors, that is, they can lie about their intentions (for example, the general says that he agrees to attack at 09:00, but does not).
The paradigm of the leader-follower, described in the task of two generals, is transformed into a commander-subordinate installation. To achieve consensus here, the commander and each subordinate must agree on the same solution (attack or retreat).

Picture translation:
The task of the Byzantine Generals. The commander general must send an order to his n-1 subordinates, such that:
- All loyal subordinate generals obey one command.
- If the commander general is loyal, then all his subordinates loyal to him obey his orders.
In addition to the second point, an interesting fact must be pointed out: if the commander is a traitor, then consensus must still be reached. As a result, all lieutenants have a majority vote.
The consensus algorithm in this case is based on the meaning of most decisions that subordinates see.
Theorem: For any m , the OM (m) algorithm reaches a consensus with more than 3m generals and a maximum of m traitors.
This means that the algorithm can reach consensus while 2/3 of the participants are honest. If the traitors are more than 1/3, consensus is not reached, the armies cannot coordinate their attacks, and the enemy wins.
OM algorithm (0)
- The commander sends his value to each of the subordinates.
- Each subordinate uses the value that he receives from the commander, or uses the value DELAY if he does not receive any value.
OM algorithm (m), m> 0
- The commander sends with his meaning to each of the subordinates.
- For each i, let vi be the value that the ith subordinate receives from the commander, or the RESET value will be used if the subordinate does not receive any value. The i-th subordinate acts as a commander in the OM algorithm (m-1) and sends a value to each of the n-2 remaining subordinates.
- For each i, provided that ji, let vj be the value that the ith subordinate received from the jth subordinate in step (2) (using the OM Algorithm (m-1)), or uses the value DELAY if doesn't get any meaning. The ith slave uses the majority value (v1, ..., vn-1).
When m = 0 there are no traitors, each subordinate follows the order. For m> 0, each final choice of a subordinate proceeds from the predominant part of the election of all subordinates.
It will be clearer if you look at the situation from the point of view of the second subordinate - let C be the Commander, and L {i} is the i-th subordinate.

OM (1): Subordinate 3 is a traitor. The situation from the point of view of the second subordinate.
Steps:
- The commander sends v to all subordinates.
- L1 sends L2 the value of v or L3 sends L2 the value of x.
- L2 ← majority (v, v, x) == v
The final decision is made from a majority of the votes of L1, L2 and L3 and as a result consensus is reached.
It is important to remember that the goal is for most subordinates to choose the same solution, rather than a specific one.
Let's look at the case when the commander is a traitor.

OM (1): The commander is a traitor.
Steps:
- The commander sends L1, L2, L3 the values of x, y, z, respectively;
- L1 sends the value of x to the slaves L2, L3 | L2 sends L1, L3 the value of y | L3 sends L1, L2 the value of z;
- L1 ← majority (x, y, z) | L2 ← majority (x, y, z) | L3 ← majority (x, y, z)
They all have the same value, so consensus is reached. Note that even if the values of x, y, z are all different, the majority value (x, y, z) is the same for all three subordinates. If x, y, z are completely different orders, we can assume that they will act according to the default plan - RESET.
To look at a practical approach to a more complex example with 7 generals and 3 traitors, I suggest you read this article .
Byzantine fault tolerance
Byzantine fault tolerance is a characteristic that defines a system that allows for a failure class that belongs to the Byzantine Generals Task. Byzantine failure is the most complex class of failure modes . It does not imply any restrictions and makes no assumptions about what kind of behavior a node can have (for example, a node can generate any arbitrary data, posing as an honest participant).
Byzantine mistakes are the hardest to fix. Byzantine fault tolerance was necessary in aircraft engine systems, in nuclear power plants, and in virtually any system whose actions depend on the results of a large number of sensors. Even SpaceX sees it as a potential requirement for its systems.
The algorithm mentioned in the previous section corresponds to Byzantine fault tolerance until the number of traitors exceeds one third of all generals. There are other options to facilitate this task, including the use of digital signatures or the introduction of restrictions on communication between peers.
How does all this relate to the blockchain?
Blockchain are decentralized ledgers that, by definition, are not controlled by the central authority. Due to the values stored in them, attackers have a good economic incentive to try to initiate a mistake. Nevertheless, the Byzantine fault tolerance and, therefore, the solution of the Byzantine generals problem for the blockchain are simply necessary.
In the absence of Byzantine Fault Tolerance, a peer can transmit and publish false transactions, completely nullifying the reliability of the blockchain. To make matters worse, there is no central authority that can take responsibility and repair damage.
When Bitcoin was invented, the big breakthrough was the use of evidence of the probabilistic solution of the Byzantine Generals problem. It was described in detail by Satoshi Nakamoto in this email .
Conclusion
In this article, we examined some basic concepts of consensus in distributed systems.
All Articles