We design a space rocket from scratch. Part 4 - Kepler's Second Law

Content

Part 1 - The task of two bodies

Part 2 - Semi-solution of the two-body problem

Part 3 - Already almost-solution of the two-body problem

Kepler's second law

Hello! Last time we settled on these equations:

\ begin {equation *}

\ begin {cases}

\ ddot {x} = - \ mu \ dfrac {x} {(x ^ {2} + y ^ {2}) ^ {\ frac {3} {2}}},

\\

\ ddot {y} = - \ mu \ dfrac {y} {(x ^ {2} + y ^ {2}) ^ {\ frac {3} {2}}}.

\ end {cases}

\ end {equation *}

The task is now flat, everything will be fine. Run the numerical simulation and draw several trajectories of motion (for different initial conditions). Not animation, as before, but to see what forms the lines have:





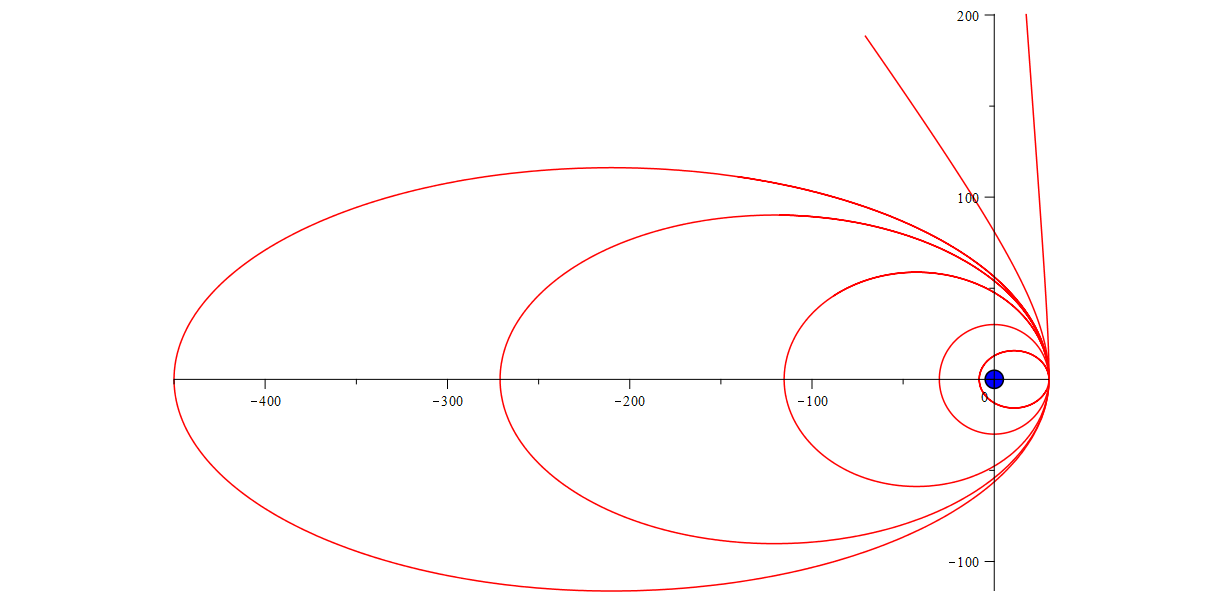
Possible satellite trajectories



Those who are familiar with ellipses will immediately say: bye, so it looks like ellipses!



And those who have not heard of ellipses will say: oval. Or a flattened circle.



But are all the lines here “ellipses”? The last two are not finished, but apparently, if you extend them, will they become closed and become very large ellipses? Well, let's extend one of them, the one in the middle.





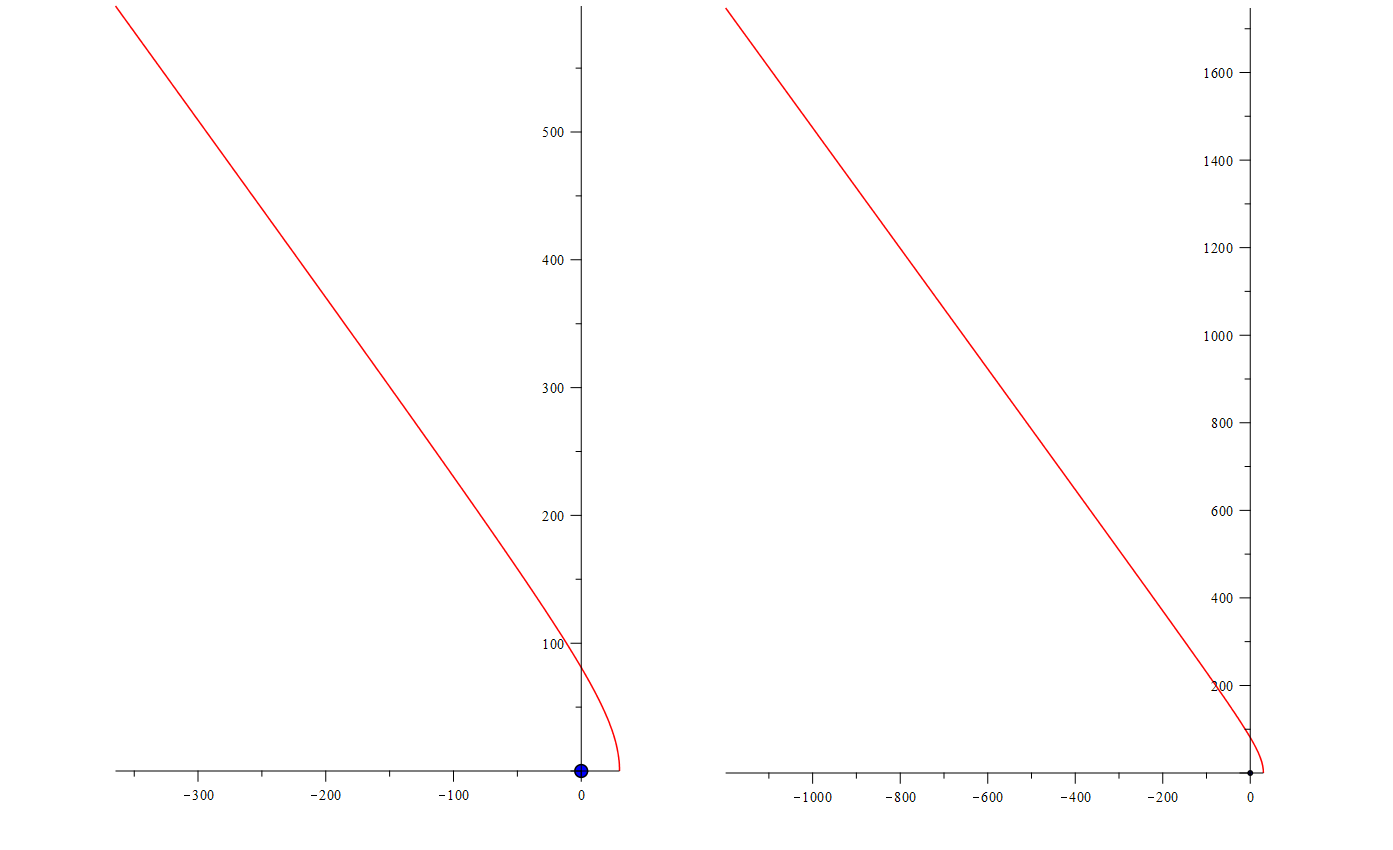
Not like an ellipse



It turns into a direct one ... It turns. Those who know the ellipse - also know the hyperbola. And just looking at the picture, I give you a word - they shouted that word with all their might. And then the thought came to them: bye, so these are conics - conical sections. Should we also wait for a parabola? And the equation will answer them: wait.



So, those who do not understand too well what is at stake - do not worry. We will explain further. While this is not important, while we just numerically modeled to figure out: what still should approximately happen.



Well, for a snack you can take another look at how a satellite flies in a plane:





animation 1: a satellite flies in an ellipse



From all these pictures and animations it is clear that even if you get an “ellipse”, it is somehow located on the side. In the sense, the center of the ellipse does not coincide with the origin. And always sideways. And you can also notice that the body moves unevenly. The closer to the origin (or a massive motionless body) - the faster it flies. Velocity versus time:





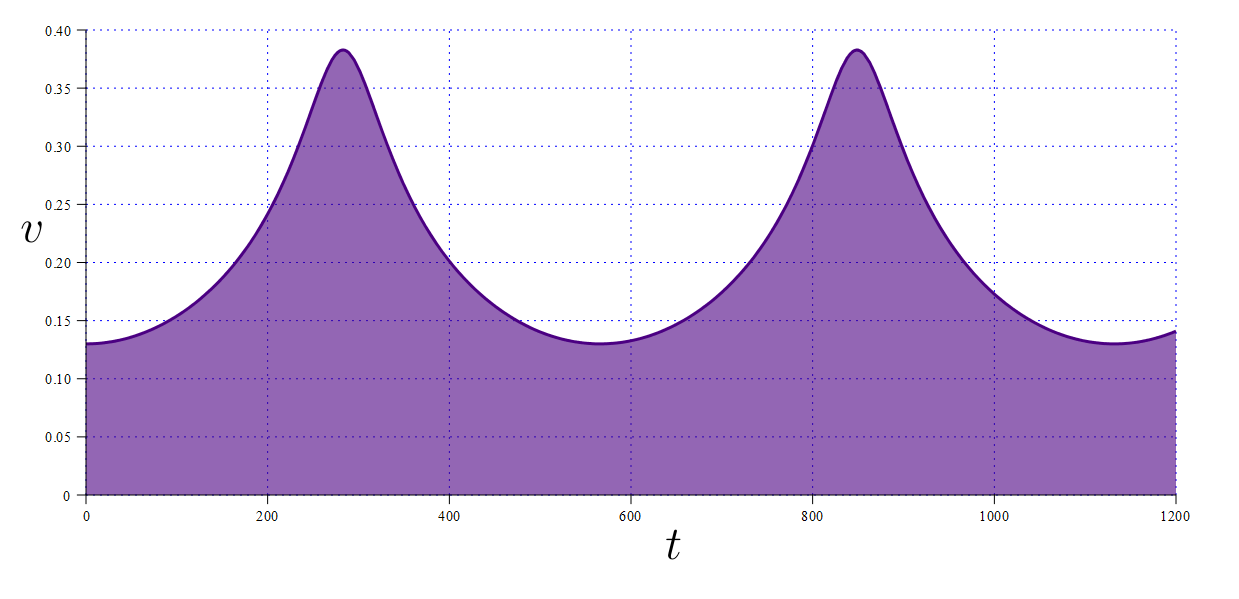
Satellite speed



Okay, we will solve the system of equations. If it is not immediately solved, then the equation does not resemble anything standard, already solved. Then apply the change of variables - the standard technique. Considering that we get closed oval shapes, and sometimes even circles, you can try to switch to polar coordinates. But this is not the main argument leading to this decision. The main one is:

$$

$$x ^ {2} + y ^ {2}$$

This thing sits on the right sides of both equations in the denominator. Also under the root. And the root itself is in the third degree.



The polar coordinates are what this is. Although I will not explain, just show:





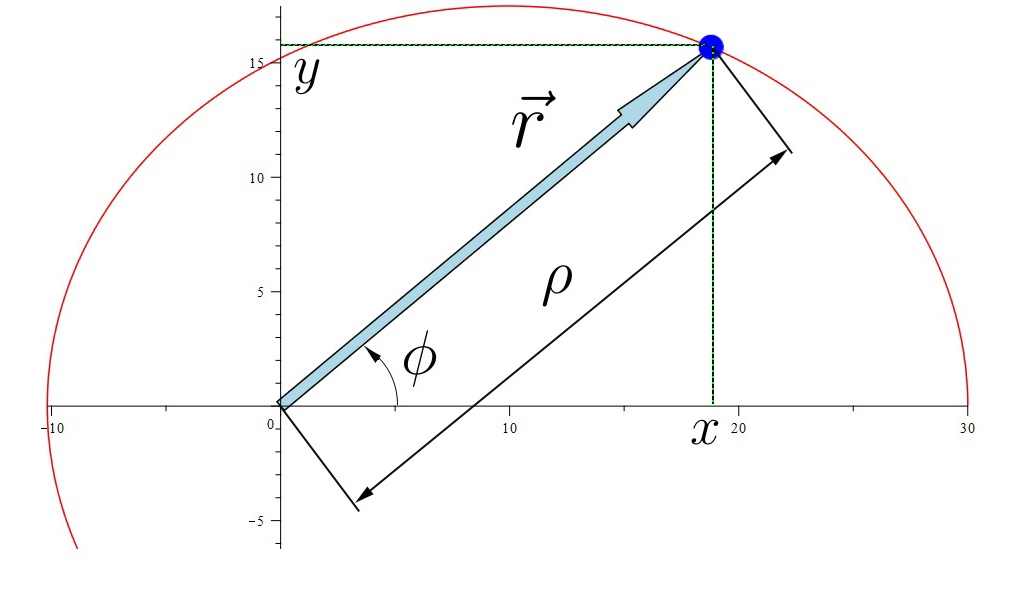
Polar coordinate system



The connection between old and new variables is easy to establish, school trigonometry:

\ begin {equation *}

\ begin {cases}

x = \ rho \ cos (\ phi),

\\

y = \ rho \ sin (\ phi).

\ end {cases}

\ end {equation *}

If you square both equations and add, it will:

$$

$$x ^ {2} + y ^ {2} = \ rho ^ {2} \ cos ^ {2} (\ phi) + \ rho ^ {2} \ sin ^ {2} (\ phi) = \ rho ^ {2} [\ cos ^ {2} (\ phi) + \ sin ^ {2} (\ phi)],$$

$$

$$\ rho ^ {2} = x ^ {2} + y ^ {2}.$$

Ah, why use the polar coordinates, then our differential equations will take the form (for starters, at least the right parts):

\ begin {equation *}

\ begin {cases}

\ ddot {x} = - \ mu \ dfrac {x} {(x ^ {2} + y ^ {2}) ^ {\ frac {3} {2}}} = - \ mu \ dfrac {\ rho \ cos (\ phi)} {(\ rho ^ {2}) ^ {\ frac {3} {2}}},

\\

\ ddot {y} = - \ mu \ dfrac {y} {(x ^ {2} + y ^ {2}) ^ {\ frac {3} {2}}} = - \ mu \ dfrac {\ rho \ sin (\ phi)} {(\ rho ^ {2}) ^ {\ frac {3} {2}}},

\ end {cases}

\ end {equation *}

and cutting back on $$$\ rho$ numerator and denominator:

\ begin {equation *}

\ begin {cases}

\ ddot {x} = - \ mu \ dfrac {\ cos (\ phi)} {\ rho ^ {2}},

\\

\ ddot {y} = - \ mu \ dfrac {\ sin (\ phi)} {\ rho ^ {2}}.

\ end {cases}

\ end {equation *}

Well, obviously, it's more pleasant to watch. And what to do with the left parts? Obviously you need to differentiate. Do not forget: $$$\ left \ lbrace \ rho (t), \ phi (t) \ right \ rbrace$ - functions of time, these are our new variables instead $$$\ left \ lbrace x (t), y (t) \ right \ rbrace$ . The task is two-dimensional, and there must be two variables. Two was - two became.





Here it is:

\ begin {equation *}

\ begin {cases}

\ ddot {\ rho} \ cos (\ phi) - 2 \ dot {\ rho} \ dot {\ phi} \ sin (\ phi) - \ rho \ ddot {\ phi} \ sin (\ phi) - \ rho \ dot {\ phi} ^ {2} \ cos (\ phi) = - \ mu \ dfrac {\ cos (\ phi)} {\ rho ^ {2}}

\\

\ ddot {\ rho} \ sin (\ phi) + 2 \ dot {\ rho} \ dot {\ phi} \ cos (\ phi) + \ rho \ ddot {\ phi} \ cos (\ phi) - \ rho \ dot {\ phi} ^ {2} \ sin (\ phi) = - \ mu \ dfrac {\ sin (\ phi)} {\ rho ^ {2}}

\ end {cases}

\ end {equation *}

What is it? It is easier? - Wait a minute!



and it turns out quite well:

\ begin {equation *}

\ begin {cases}

\ ddot {\ rho} = - \ dfrac {\ mu} {\ rho ^ {2}} + \ rho \ dot {\ phi} ^ {2} \\

\ ddot {\ phi} = - \ dfrac {2 \ dot {\ rho} \ dot {\ phi}} {\ rho}

\ end {cases}

\ end {equation *}

So there is no need to grumble ahead of time, God always leads us in the right way. Always.



Well, take a closer look at the second equality:

$$

$$\ dfrac {d \ dot {\ phi}} {\ cancel {dt}} = - \ dfrac {2 \ dot {\ phi}} {\ rho} \ dfrac {d \ rho} {\ cancel {dt}}$$

It is possible to integrate a little:

$$

$$\ dfrac {d \ dot {\ phi}} {\ dot {\ phi}} = -2 \ dfrac {d \ rho} {\ rho}$$

$$

$$\ int \ dfrac {d \ dot {\ phi}} {\ dot {\ phi}} = -2 \ int \ dfrac {d \ rho} {\ rho}$$

Elementary integrals, and do not forget the constant:

$$

$$\ ln {\ dot {\ phi}} = -2 \ ln {\ rho} + \ ln {h}$$

Elementary school transformations:

$$

$$\ ln {\ dot {\ phi}} + \ ln {\ rho ^ {2}} = \ ln {h}$$

$$

$$\ ln {\ dot {\ phi} \ rho ^ {2}} = \ ln {h}$$

$$

$$\ dot {\ phi} \ rho ^ {2} = h$$

No, not like that. Like this:

$$

$$h = \ rho ^ {2} \ dot {\ phi}$$

You will say: well, why we wrote down a constant in the form of a logarithm - of course. But why do we have a constant - $$$h$ ?? Constants are always - $$$C$ !



And I will answer the people:







Jehovah God says this: Remember, Israel, about the momentum you received in the last article :

$$

$$\ vec {h} = [\ vec {r}, \ dot {\ vec {r}}]$$

So, but we are already in the new coordinate system. There are vectors in it $$$\ vec {h}, \ vec {r}$ will have such components:

$$

$$\ vec {h} = (0, 0, h)$$

$$

$$\ vec {r} = (x, y, 0)$$

As agreed earlier - we do not write strokes. A vector $$$\ vec {h}$ is perpendicular to the plane of rotation, naturally it will have only one component, and is equal to its length. Vector $$$\ vec {r}$ on the contrary, lies in this plane and there are two components.



And now, if we add the polar coordinate system that we are working on now, it’s interesting to practice:

$$

$$\ vec {r} = \ left [\ rho \ cos (\ phi), \ rho \ sin (\ phi), 0 \ right]$$

$$

$$\ dot {\ vec {r}} = \ left [\ dot {\ rho} \ cos (\ phi) - \ rho \ sin (\ phi) \ dot {\ phi}, \ dot {\ rho} \ sin (\ phi) + \ rho \ cos (\ phi) \ dot {\ phi}, 0 \ right]$$

And then something obviously interesting should turn out:

$$

$$h \ vec {k} = \ begin {vmatrix} \ vec {i} & \ vec {j} & \ vec {k} \\ \ rho \ cos (\ phi) & \ rho \ sin (\ phi) & 0 \\ \ dot {\ rho} \ cos (\ phi) - \ rho \ sin (\ phi) \ dot {\ phi} & \ dot {\ rho} \ sin (\ phi) + \ rho \ cos (\ phi) \ dot {\ phi} & 0 \ end {vmatrix} =$$

$$

$$= 0 \ vec {i} + 0 \ vec {j} + \ begin {vmatrix} \ rho \ cos (\ phi) & \ rho \ sin (\ phi) \\ \ dot {\ rho} \ cos (\ phi) - \ rho \ sin (\ phi) \ dot {\ phi} & \ dot {\ rho} \ sin (\ phi) + \ rho \ cos (\ phi) \ dot {\ phi} \ end {vmatrix} \ vec {k}$$

Obviously:

$$

$$h = \ rho \ cos (\ phi) \ left (\ dot {\ rho} \ sin (\ phi) + \ rho \ cos (\ phi) \ dot {\ phi} \ right) - \ rho \ sin ( \ phi) \ left (\ dot {\ rho} \ cos (\ phi) - \ rho \ sin (\ phi) \ dot {\ phi} \ right) =$$

$$

$$= \ xcancel {\ rho \ dot {\ rho} \ sin (\ phi) \ cos (\ phi)} + \ rho ^ {2} \ dot {\ phi} \ cos ^ {2} (\ phi) - \ xcancel {\ rho \ dot {\ rho} \ sin (\ phi) \ cos (\ phi)} + \ rho ^ {2} \ dot {\ phi} \ sin ^ {2} (\ phi) =$$

$$

$$= \ rho ^ {2} \ dot {\ phi} [\ sin ^ {2} (\ phi) + \ cos ^ {2} (\ phi)] = \ rho ^ {2} \ dot {\ phi}$$

And Nuka now compare the equalities we have obtained:

\ begin {equation *}

\ begin {cases}

h = \ rho ^ {2} \ dot {\ phi} \\

h = \ rho ^ {2} \ dot {\ phi}

\ end {cases}

\ end {equation *}

Here is such a coincidence.

Ok, let's take a closer look at what this expression can mean. All the same, the God of prophecy gave us about him, it is clearly important. And also, neither more nor less is one of the first integrals of our system.



Vector Product Module $$$h$ - the essence is the area of ​​the parallelogram stretched over the vector in brackets $$$[\ vec {r}, \ dot {\ vec {r}}]$ . Area…



Wait, what dimension? $$$\ rho ^ {2} \ dot {\ phi}$ :

$$

$$\ text {m} ^ {2} \ cdot \ dfrac {\ text {rad}} {c} = \ dfrac {\ text {m} ^ {2}} {c}$$

Meters squared divided by second. Area per unit of time ... Area, polar coordinates, time; God let us know what it is!



And, google the area in polar coordinates, for a long time it was in the first year, the beginning of matana:

$$

$$S = \ dfrac {1} {2} \ int \ rho ^ {2} d \ phi$$

All clear ( $$$h$ constant, do not forget):

$$

$$\ rho ^ {2} \ dot {\ phi} = \ rho ^ {2} \ dfrac {d \ phi} {dt} = h,$$

$$

$$\ rho ^ {2} d \ phi = hdt,$$

$$

$$\ int \ rho ^ {2} d \ phi = h \ int dt = ht + C,$$

Then the area:

$$

$$S = \ dfrac {1} {2} (ht + C)$$

Well, another constant $$$C$ - this is, in principle, the initial area, or half, or rather two. Let at zero time point we have 0:

$$

$$S = \ dfrac {ht} {2}$$

or the rate of change of area is constant:

$$

$$\ dot {S} = \ dfrac {h} {2}$$

It turns out beautifully - the area grows linearly. Evenly. Although the body moves, as we have seen, not at all evenly. Especially when the ellipse. Well, this is logical, because our area (in polar coordinates) comes out by “sweeping” the radius of the vector:



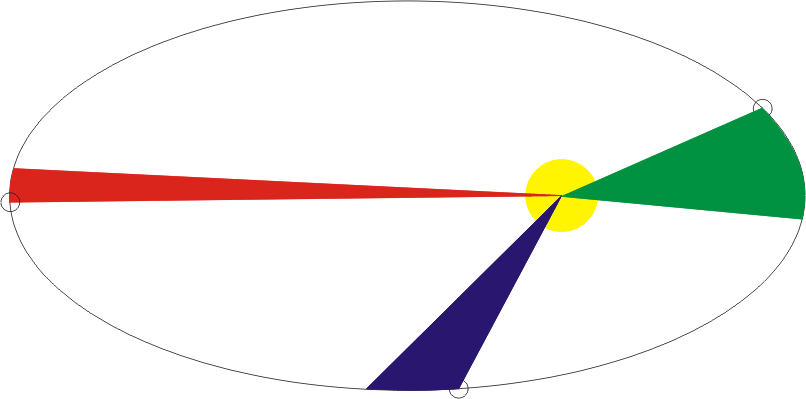
For equal periods of time, equal areas are obtained, a beautiful picture from Wikipedia



And so the body needs to fly the faster, the closer to the center of rotation, and the slower the farther. Only then will our “triangles” have equal areas.



And maybe someone will not believe it, but you and I have just, with the help of a pen, a piece of paper and a matan, discovered Kepler’s Second Law. This is one of three laws discovered empirically, intuitively selected by Johannes Kepler based on an analysis of astronomical observations by Tycho Brahe. He (Johann) did it around 1607 and it sounds like this:

Each planet moves in a plane passing through the center of the Sun, and for equal periods of time, the radius vector connecting the Sun and the planet sweeps equal areas.

And you won’t believe it, maybe, but the second law was discovered by Kepler before the first. Like ours. But he did it empirically.



Oh, there are too many coincidences ... Newton also has his own laws, his second law is also a little more important than the first, and this follows from the second.



And here is what Kepler said about astronomy and astrology:

Of course, this astrology is a dumb daughter; but, my God, where would her mother go, wise astronomy, if she did not have a silly daughter! After all, the light is still much dumber and so stupid that for the benefit of this old rational mother, a stupid daughter must chat and lie. And the salary of mathematicians is so insignificant that the mother would probably starve if her daughter did not earn anything.

Kepler understood God, understood the unity of the world. And God, too, told the Jews 3,000 years before that astrology was huh. Ventriloquism - hu * nya. All huh nya, Misha, do science. And why modern children do not like veruns. It's simple - no one looks into the Bible.



But let's go further. Want to hear how Kepeler’s first law sounds?

Each planet of the solar system is drawn in an ellipse, in one of the foci of which is the sun.

We can say that we partially discovered the first one: we know that the body rotates in an unchanged plane (and the ellipse, by definition, is a flat curve), but so far, unfortunately, we still do not know that this is an “ellipse”. And that his “focus” is just in the center of coordinates. Everything will be, but later, we'll talk about conic sections, and about ellipses, and about their tricks.



We’ll finish now, but before that I’ll throw up the hook, sorry in your mouth, on the cheek:

$$

$$\ rho ^ {2} \ dot {\ phi} = h$$

$$

$$\ dot {\ phi} = \ dfrac {h} {\ rho ^ {2}}$$

And now hocus pocus (this is the first equation from our system):

$$

$$\ ddot {\ rho} = - \ dfrac {\ mu} {\ rho ^ {2}} + \ rho \ dot {\ phi} ^ {2}$$

$$

$$\ ddot {\ rho} = - \ dfrac {\ mu} {\ rho ^ {2}} + \ rho \ left (\ dfrac {h} {\ rho ^ {2}} \ right) ^ {2}$$

Voila!

$$

$$\ ddot {\ rho} = - \ dfrac {\ mu} {\ rho ^ {2}} + \ dfrac {h ^ {2}} {\ rho ^ {3}}$$

No, well, it’s already possible to try to decide, beautifully. In the next post we will continue to decide ...



PS: It’s sad that there is no \ usepackage {cancel} module on Habr, but it may appear, I won’t fix some formulas for now. Or is it in mathjax there is no module, I do not understand, then claims to mathjax