How quantum entanglement will help in the detection of gravitational waves
We recently did an experiment to test a new approach to reducing quantum noise in LIGO and wrote an article about it, see arXiv: “Demonstration of interferometer enhancement through EPR entanglement” . And here I will tell you what quantum noises are in LIGO, how they can be reduced, and what does quantum entanglement and squeezed light have to do with it.
I talked about how the detector works and what noise there are in it in detail in the last publication about the Einstein Telescope . The detector has a wide variety of noises: seismic, thermal, quantum, and others - and all of them interfere with the registration of a signal from gravitational waves.
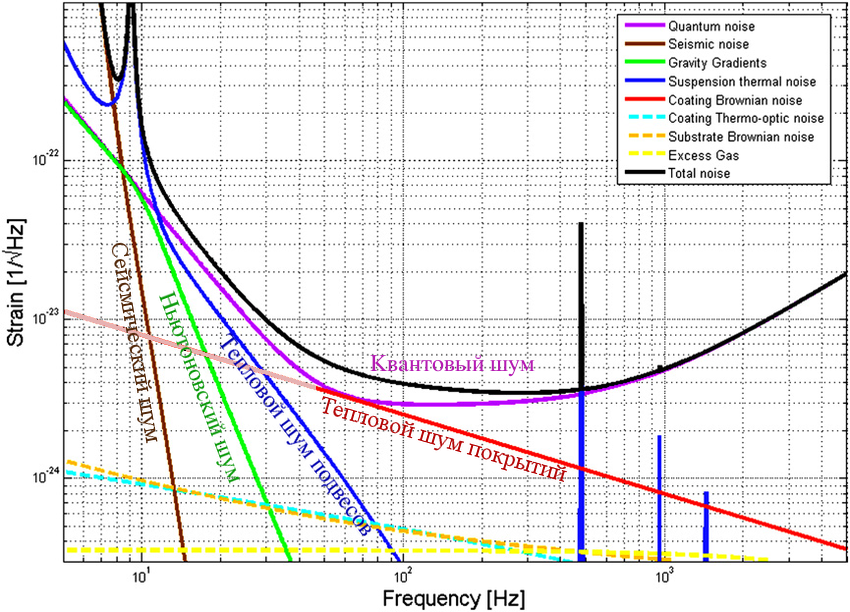
The main contributions to the sensitivity of LIGO at different frequencies, normalized to the amplitude of the GW (strain).
The whole difficulty in creating a gravitational-wave detector is to reduce these noises. Most of these noises are not fundamental, but rather technical limitations. And only quantum noises arise from the very nature of the measuring apparatus. They will become the main obstacle to better sensitivity in future detectors, so we will dwell on them in more detail. There are two quantum noises: shot noise and radiation pressure noise.
Shot noise arises due to the quantum nature of the laser: the laser beam consists of photons flying with different random delays between each other. When these photons are measured on photodiodes, fluctuations in the photon flux lead to current fluctuations and, as a result, to noise in the signal that we observe.
The noise of radiation pressure is the second side of the quantum nature of light. As is known from classical electromagnetism since the time of Lebedev’s experiments, an object on which light shines experiences pressure of light . It is easy to understand if we consider a photon as a particle: each particle carries an impulse, which is transmitted to the body upon impact. That is, when the laser shines on a movable mirror, the mirror begins to shift under the influence of light pressure. And since the photons are distributed randomly, sometimes more photons arrive at the mirror during a given time interval, sometimes less, and this light pressure force is also random. So: the quantization of light leads to a random force acting on the mirrors in LIGO. This force causes a random shift of the mirrors, which is recorded at the output of the interferometer as a spurious signal.
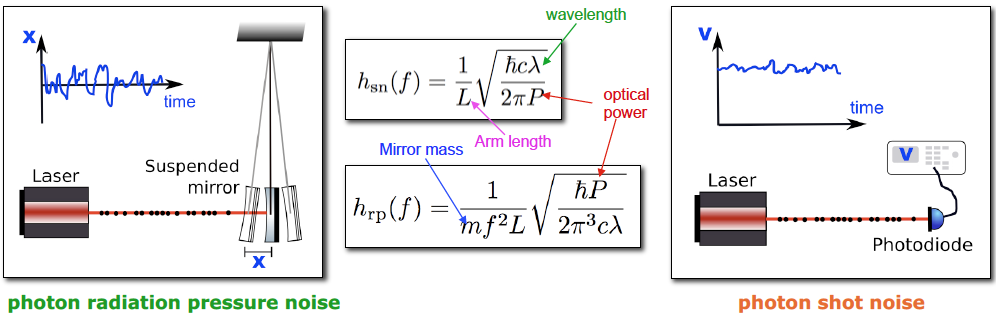
Explanation about quantum noise. A random distribution of the number of photons produce a random force of radiation pressure (left). On the other hand, a random distribution of photons in time leads to amplitude fluctuations at the photodetector (right). Both noise depend on wavelength, light power and shoulder length. The noise of radiation pressure is less, the greater the mass of mirrors. Credit: [1].
The noise of radiation pressure is stronger, the greater the power of light incident on the mirrors (i.e., the flux of photons). The signal from the GW also increases with increasing light power in the detector. The shot noise normalized to the signal decreases. As a result, it turns out that you can increase the sensitivity limited by shot noise by increasing the power of light, but you will have to pay for it with increasing noise of radiation pressure. And vice versa. There is no way in the classical way to suppress both quantum noise at once. Will have to use quantum technology.
Dependence of sensitivity on light power: shot noise (blue) decreases, and radiation pressure noise (green) increases proportionally.
There is a wonderful article on Habré about squeezed light by qbertych . If you do not know what compressed light is, I highly recommend that you first read his article. I will be brief.
If you look at the light as a wave, the characteristic parameters will not be the photon flux and the delay between them, but the amplitude and phase of the wave. Usually they talk about phase and amplitude quadratures of light.
If the signal of interest to us is contained in the phase of light, and it is small enough, then we can make an approximation:
Therefore, the value Ef called phase quadrature - it contains information about the phase.
Accordingly, shot noise is a fluctuation of the phase of light, and the noise of radiation pressure is caused by amplitude fluctuations.
Uncertainty in phase and uncertainty in amplitude are related by the Heisenberg relation:
In a conventional laser beam, these uncertainties are equal. However, it is possible to compress the phase uncertainty by increasing the amplitude uncertainty - the main thing is that their product satisfies the uncertainty relation. Such light is called squeezed:
where r is the compression ratio.
Generally speaking, even in the absence of a powerful beam, vacuum fluctuations always exist. They can also be compressed to obtain a compressed vacuum: on average, the number of photons in it is zero, but the fluctuations of the amplitude and phase are compressed.
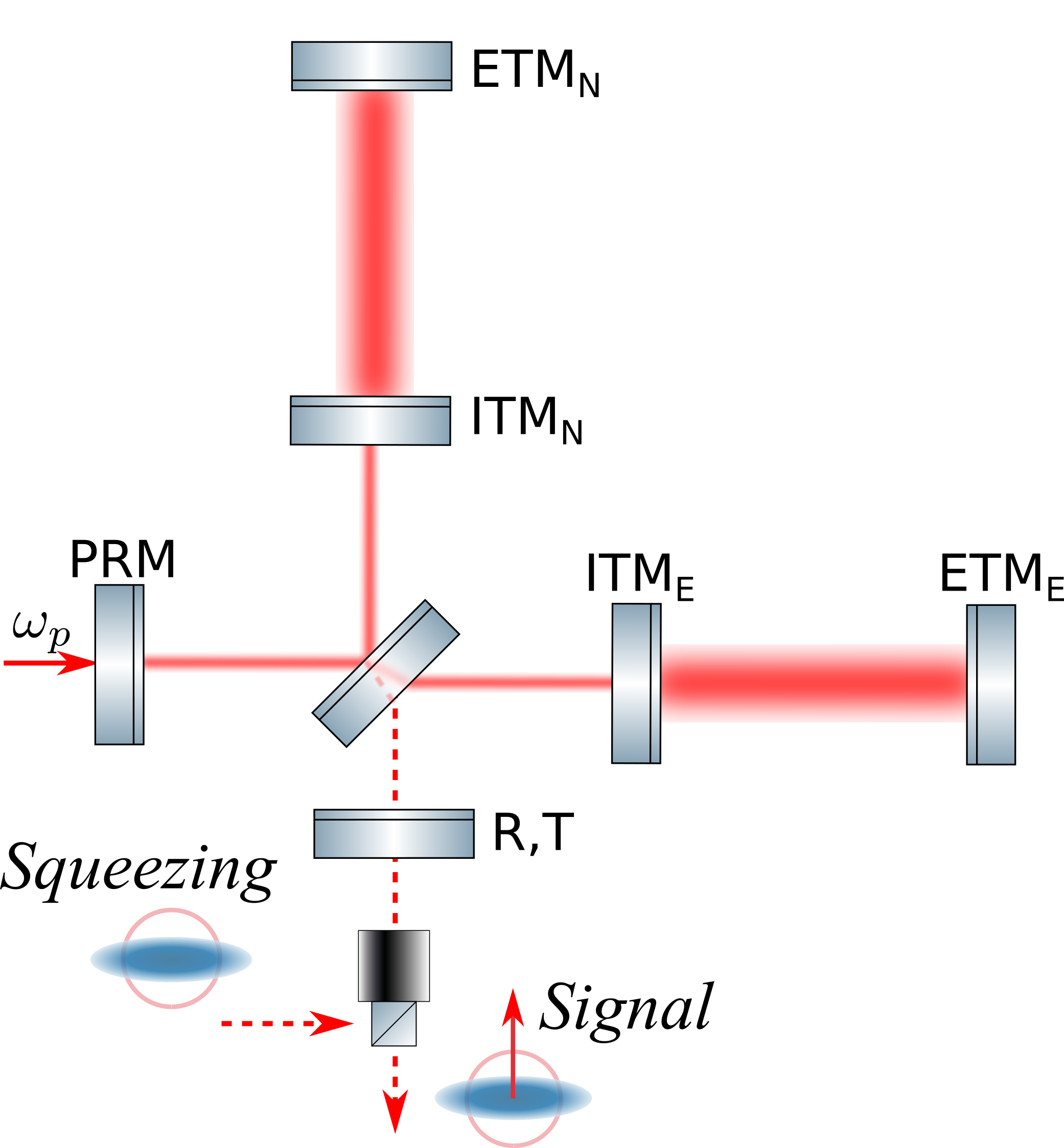
It is the vacuum fluctuations entering the detector through the signal port that are the source of quantum noise in LIGO. Therefore, if this vacuum is compressed in phase, this will reduce shot noise in the detector.
This approach has been used in the GEO600 detector for the past 8 years, reducing shot noise by four times, and since this year it has also been implemented in LIGO, reducing shot noise by half (which increases the number of recorded events by 8 times).


Left: An example of improved LIGO sensitivity with squeezed light. Right: the best compression to date was created in our group several years ago: vacuum fluctuations were suppressed by 15 dB.
However, everything is not so simple: according to the uncertainty relation, if we compress the phase, we increase the fluctuations in amplitude. And they increase the noise of radiation pressure. And again you have to choose which noise to reduce by increasing the other. But is it possible to somehow get around this limitation?
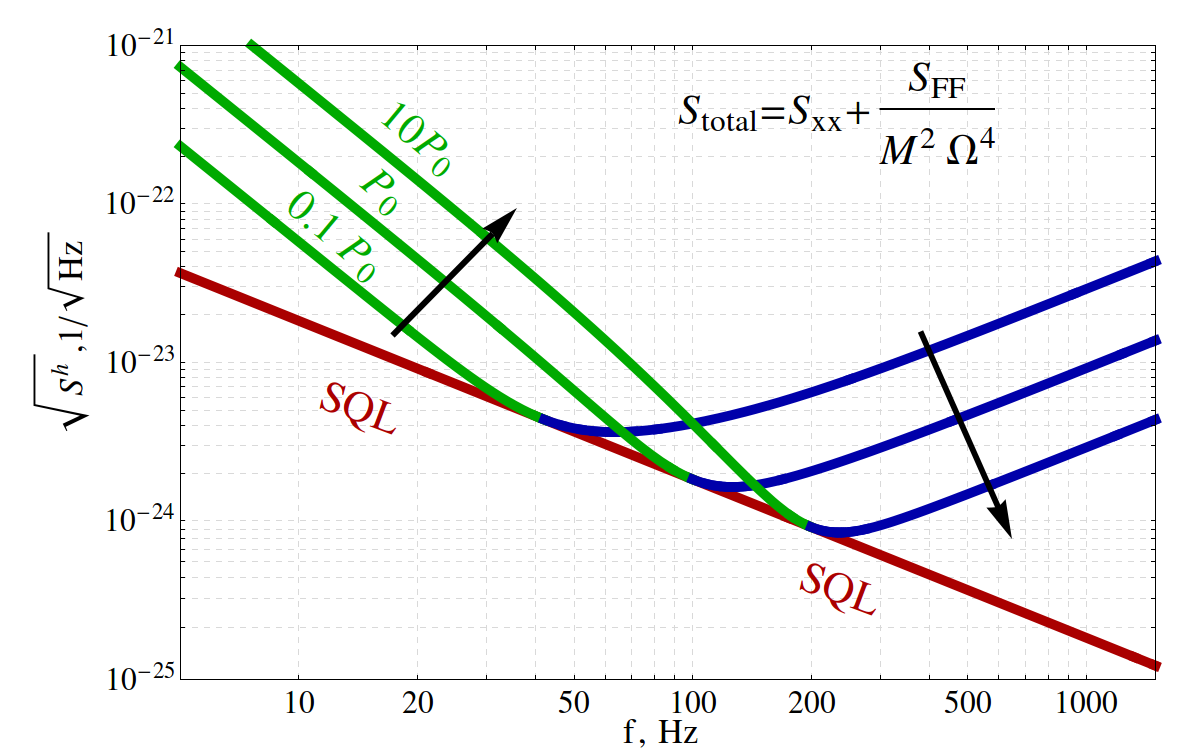
Fortunately, two quantum noise limits the sensitivity of the detector at different frequencies: at low noise the radiation pressure is much stronger than shot pressure, and at high - vice versa. Therefore, it is possible to prepare a tricky compression of light, where at low frequencies the light is compressed in amplitude (and therefore the radiation pressure noise decreases), and at high frequencies - in phase (and therefore shot noise is reduced).
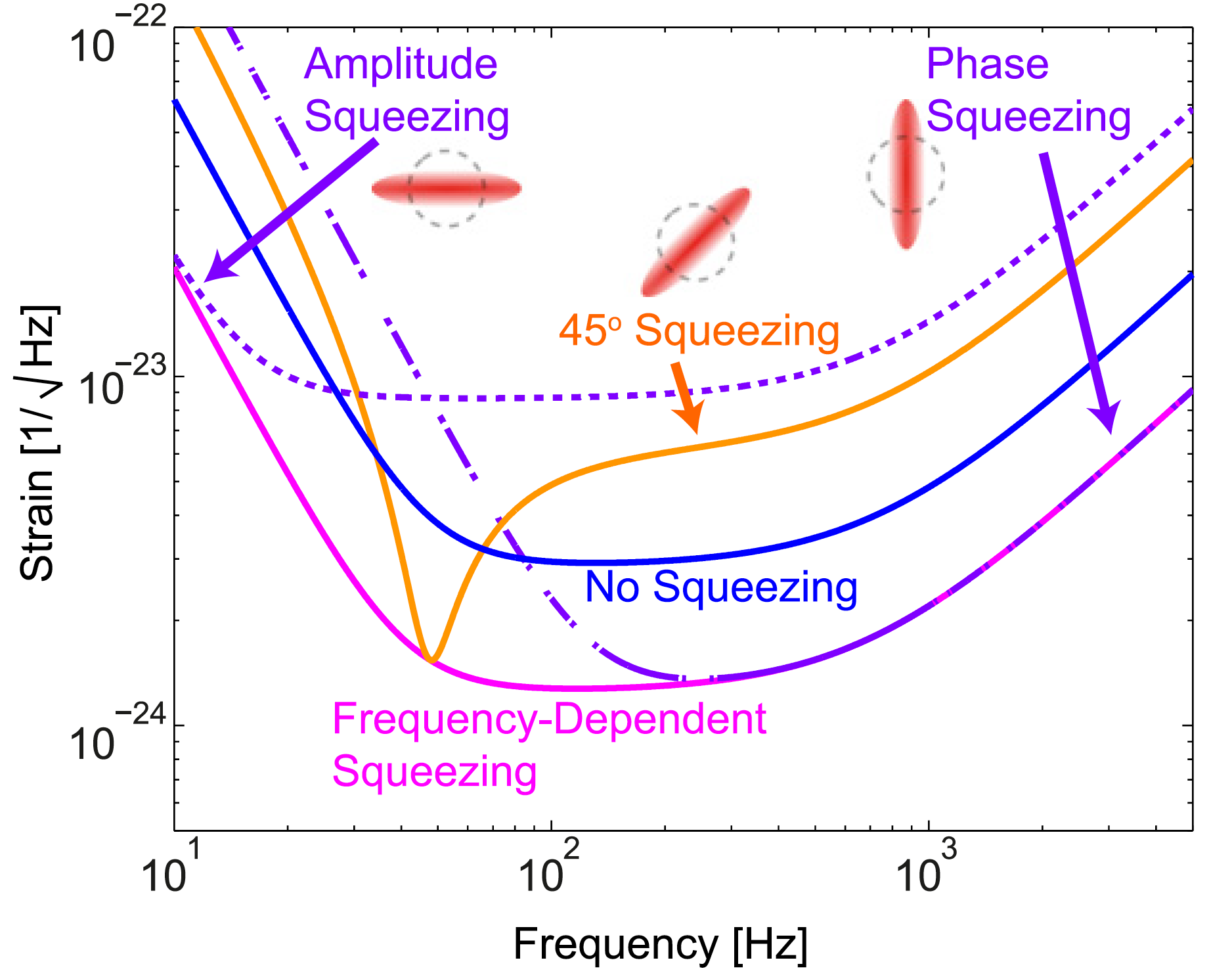
Frequency-dependent compression: at different frequencies, the amplitude, phase, or a combination thereof is compressed. As a result, sensitivity is improved at all frequencies. [SSY Chua et al 2014 Class. Quantum Grav. 31 183001]
Fundamentally, the reason for the need for frequency-dependent compression is that the radiation pressure on the mirrors also creates light compression, but in a different quadrature. This can be seen in the image below: if you use conventional compression at the input, at the output it acquires a frequency dependence due to radiation pressure. To "cancel" this frequency dependence, you need to set the inverse dependence for compression at the input.
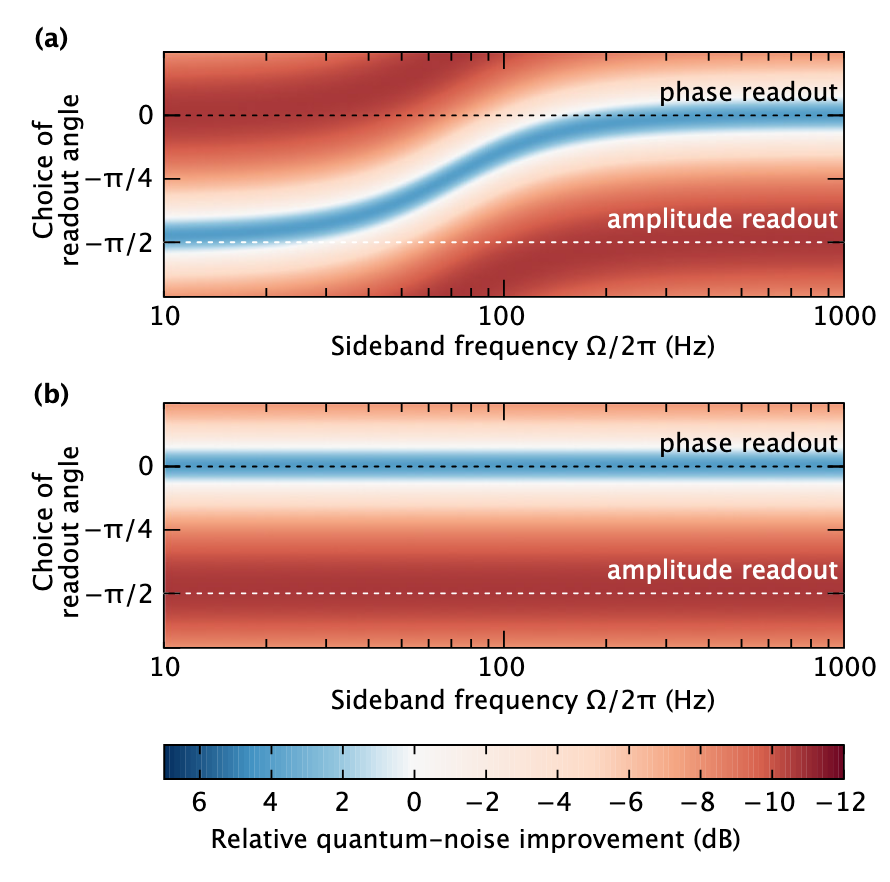
An example from the article: the dependence of improving the sensitivity of the interferometer when using conventional compression as a function of frequency and different measurement phases is shown above - the signal is in phase quadrature, and it can be seen that if the sensitivity increases at high frequencies (blue color), then at low frequencies it decreases (red ) Using frequency-dependent compression can improve sensitivity at all frequencies.
So, conceptually the problem of reducing quantum noise at all frequencies is solved, the question remains: how to implement such a frequency dependence. To do this, you need to figure out how to turn the compressed phase into a compressed amplitude. Actually, it’s very simple: to produce a phase shift:
Usually, a simple mirror is enough to phase shift, which will change the length of the path traveled by the light. However, in this case, you need a device that will create a frequency-dependent phase shift: do not shift the phase at high frequencies, but shift at low p i / 2 .
Currently, the leading concept of creating frequency-dependent compression in all designs of future detectors is the use of additional filtering resonators. If the compressed vacuum is reflected from such a resonator when it is detuned from the resonant frequency, it will acquire the necessary frequency dependence. However, it has great difficulty: in order to create the required frequency dependence, the resonators must be several hundred meters long in a vacuum, and this is very expensive and difficult to control. We have another idea.
The fact is that in the detector itself there are already many resonators of suitable sizes, low losses and a well-known control method, but they cannot be used directly - for frequency-dependent compression, it is necessary to detun from resonance. But each resonator has many resonant frequencies, while the detector only works on one of them. The idea is to use a different resonance, reflecting the squeezed light from the interferometer itself to obtain the necessary frequency dependence. The question remains: how to use the frequency dependence created at a frequency different from the main working frequency of the laser. And then quantum entanglement comes to the rescue.
The question of the nature of entanglement is undoubtedly worthy of a separate article. I discussed a little more intricacy in a previous article on the Habré, so here I will only briefly describe its main properties. Let's start with the EPR paradox (Einstein-Podolsky-Rosen): three gentlemen noticed that there is a catch in quantum mechanics. On the one hand, there is the uncertainty principle, which says that it is impossible to accurately measure the coordinate and momentum of a particle at the same time (and in our case, the amplitude and phase of light). On the other hand, one can make such a simple experiment: take the particle decay event in which two identical particles are born. According to the law of conservation of momentum, they will scatter in opposite directions at the same speed. If we measure the momentum of one particle, we will know exactly the momentum of the second. If we measure the coordinate of the second particle, we will simultaneously know exactly both the coordinate (we measured it) and the momentum (we predicted it from the measurement of the first particle), which, it would seem, is impossible due to the uncertainty relation. The visible paradox is solved by introducing the concept of entanglement of particles: two particles are not independent of each other, they are described by one wave function. This wave function is nonlocal: until the moment of measurement it is impossible to say which of the particles flew in which direction. In a sense, they both flew in both directions at once, and only at the moment of measurement there was a random choice of which particle was measured. Their coordinates and momentum are connected so that the uncertainty relation does not apply to their relative value. Moreover, if one of the particles is acted upon, for example by some force, the second particle will also “feel” this force - its measured parameters will change accordingly.
So, for us the most important thing: if we have two particles, we can accurately predict the properties of the second particle by measuring the first. We can put a source of influence on the path of one particle, and it will act on two at once. Having made the correct measurement, we can see the result of this effect.
How we use it (it was proposed for the first time in an article in Nature Physics [2]). The role of particles in the EPR is played by two beams of compressed vacuum at two frequencies: the fundamental frequency of the interferometer and the frequency of the next resonance of the resonator. We confuse them, one of them (high frequency) is reflected from the tuned resonator and measured. He gets a frequency dependence. Since the rays are entangled, this frequency dependence is also transmitted to the beam at the fundamental frequency. After measurement, we can predict the signals in the main beam ideally with perfect accuracy. To do this, we separately measure on two separate detectors, and optimally process the data.
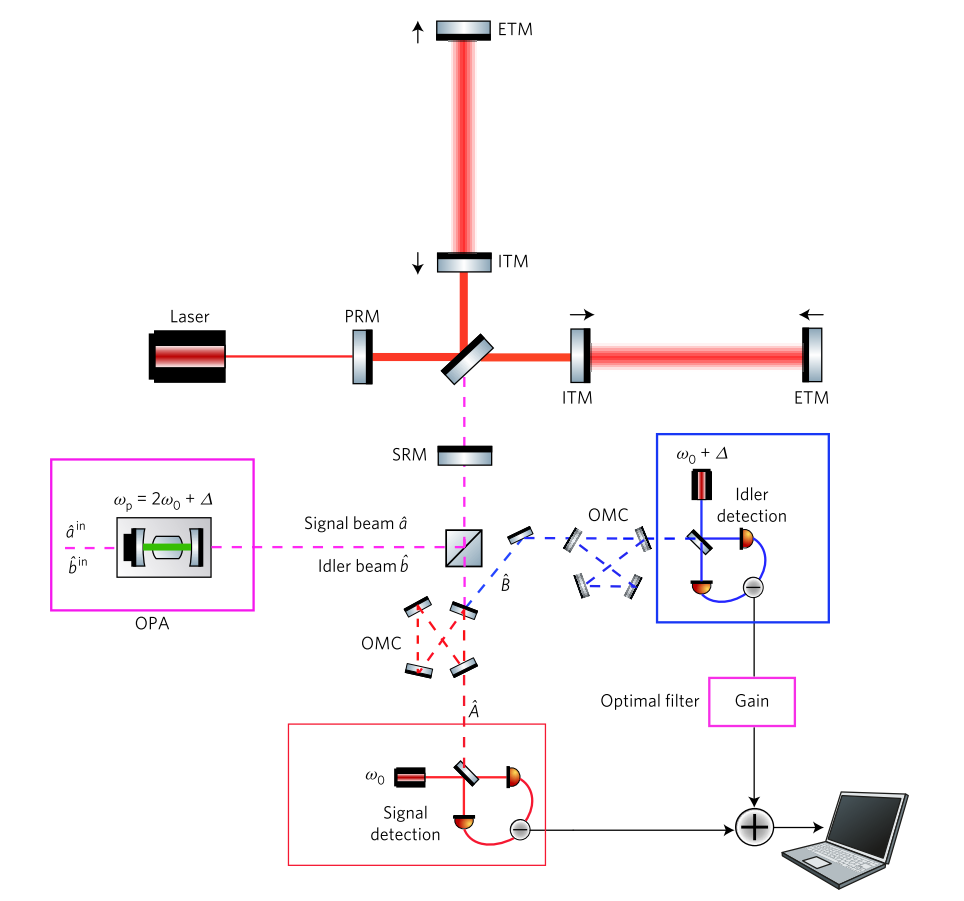
A complete frequency-dependent compression scheme based on entanglement from [2]. OPA (Optical Parametric Amplifier) creates two entangled beams of compressed vacuum at different frequencies, both of which are sent to the detector. A beam at the carrier frequency resonates in the interferometer. A beam at a high frequency is detuned from one of the higher resonances. At the output, the rays are separated and detected on two different homodyne detectors, after which they are processed in an optimal way.
Our experiment does not include a full interferometer with moving mirrors. Instead, we are exploring the possibility of obtaining frequency-dependent compression using entangled light reflected from a resonator.
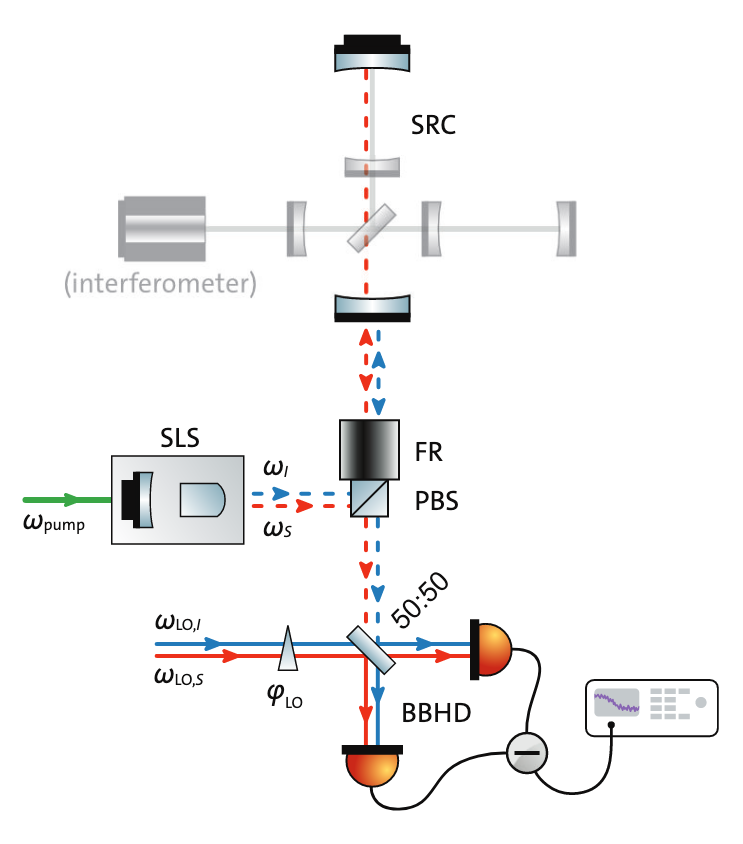
Simplified experimental design. Instead of a full interferometer, we have one 2.5m long optical resonator. Instead of two different homodyne detectors, we use one detector, but two reference beams of different frequencies.
As I wrote above, in an interferometer, radiation pressure creates a frequency dependence of compressed light, which spoils the sensitivity of the detector. In order to cancel this frequency dependence, we need to create an inverse frequency dependence of the squeezed light. In our experiment, the sensitivity spoils not the radiation pressure (we do not have moving mirrors), but the detuning of the detector from resonance (see the picture below (a)). When measured in a signal readout (phase readout), this spoils the sensitivity at low frequencies (red).
To restore sensitivity, we rebuild an additional ray (idler) from resonance in the opposite direction. Then after measurement, we can completely restore sensitivity. In terms of EPR - we can predict the result of measuring the phase quadrature with better accuracy using quantum entangled light.
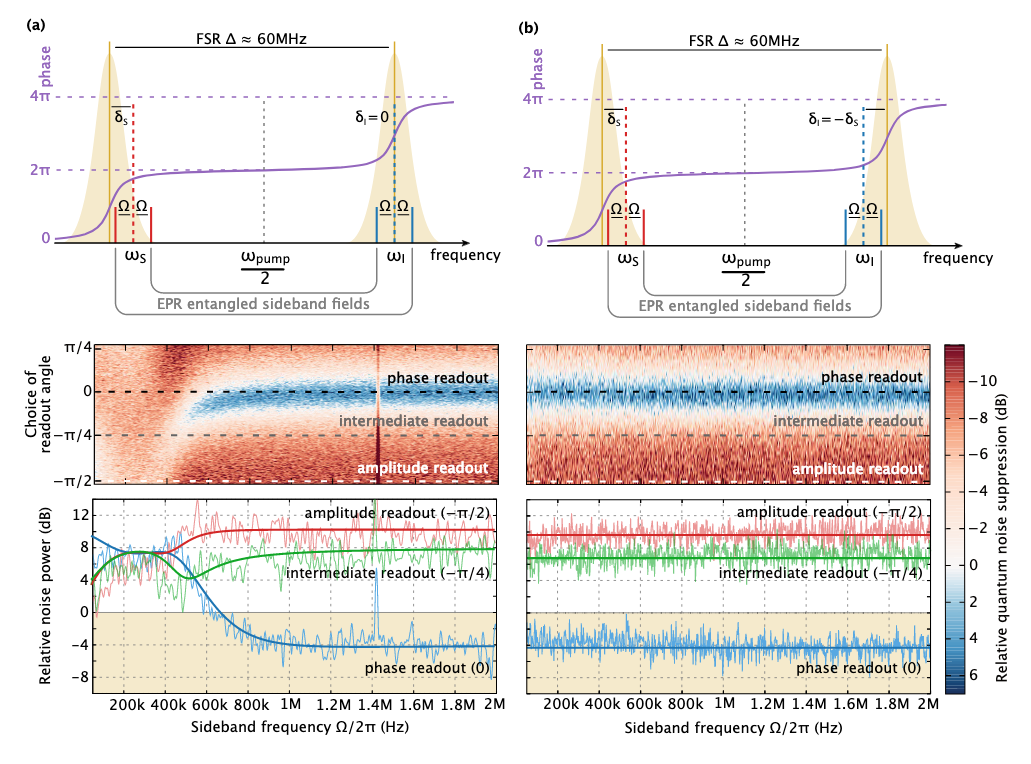
Two experiments to observe frequency-dependent compression. In the first (a), we built up the signal beam from the resonance of the detector, thereby spoiling the sensitivity in the phase quadrature (and creating a frequency dependence of the squeezed light). In the second, we created an additional frequency dependence for the second ray (idler) and due to quantum entanglement between the two rays, signal and ilder were able to restore the damaged sensitivity by canceling the frequency dependence introduced in the first experiment.
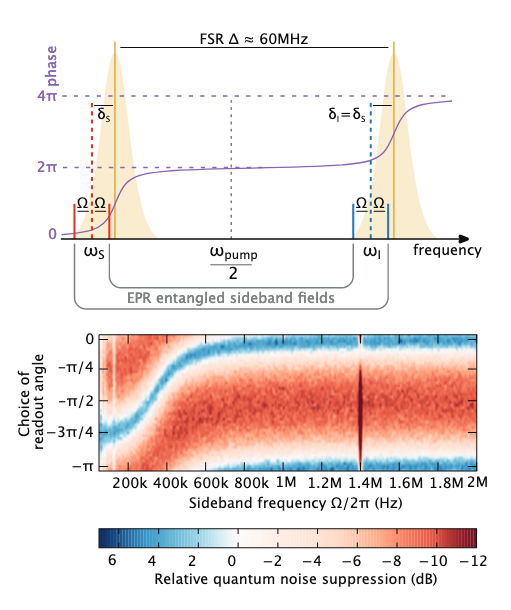
In the image above, the frequency dependence in (a) is rather blurry. This is due to limitations in post-processing: ideally, two separate homodyne detectors are needed, the signals from which can be filtered optimally. However, in another mode, we can obtain a beautiful frequency dependence of the squeezed light if we rebuild both rays from resonance in one direction. Such a scheme is not relevant for the detector, but gives an idea of the installation options. Well, just beautiful experimental data :)
To summarize. Quantum fluctuations of light are the main and most fundamental source of noise in all modern and future detectors. To suppress them, one can use quantum correlations - squeezed light. However, in order to reduce noise in the entire frequency range of the detector, it is necessary to compress amplitude fluctuations at low frequencies and phase fluctuations at high frequencies. Such frequency-dependent compression is proposed to be carried out using special filtering resonators. Traditionally, such resonators are very expensive and difficult to implement. Our alternative is to use the detector itself as a filter resonator, using quantum entangled light. We made an experiment and showed that quantum entanglement actually allows to realize this idea.
This approach is not a panacea, alas: you have to pay for convenience. For the concept to work fully, it is necessary to use two homodyne detectors, which is quite difficult experimentally. In addition, the second detector adds noise to the sensitivity - albeit much less than you can gain from compression.
In this work, we played around with intricacies and squeezed light and showed how we can use them to improve the sensitivity of future detectors. But this, of course, is only the first step on a long road to implementing this approach in a real detector: you need to check how everything works with a real interferometer, with moving mirrors, two homodyne, and so on. In general, the work is still full.
For those interested in the details, see our article and the article where the idea was first presented [2].
[1] S. Hild Beyond 2nd Generation GW detectors
[2] Y. Ma et al, Proposal for gravitational-wave detection beyond the standard quantum limit through EPR entanglement, Nature Physics volume 13, pages 776–780 (2017)
And now some news about LIGO:

1. LIGO sensitivity and quantum noise
I talked about how the detector works and what noise there are in it in detail in the last publication about the Einstein Telescope . The detector has a wide variety of noises: seismic, thermal, quantum, and others - and all of them interfere with the registration of a signal from gravitational waves.

The main contributions to the sensitivity of LIGO at different frequencies, normalized to the amplitude of the GW (strain).
The whole difficulty in creating a gravitational-wave detector is to reduce these noises. Most of these noises are not fundamental, but rather technical limitations. And only quantum noises arise from the very nature of the measuring apparatus. They will become the main obstacle to better sensitivity in future detectors, so we will dwell on them in more detail. There are two quantum noises: shot noise and radiation pressure noise.
Shot noise arises due to the quantum nature of the laser: the laser beam consists of photons flying with different random delays between each other. When these photons are measured on photodiodes, fluctuations in the photon flux lead to current fluctuations and, as a result, to noise in the signal that we observe.
The noise of radiation pressure is the second side of the quantum nature of light. As is known from classical electromagnetism since the time of Lebedev’s experiments, an object on which light shines experiences pressure of light . It is easy to understand if we consider a photon as a particle: each particle carries an impulse, which is transmitted to the body upon impact. That is, when the laser shines on a movable mirror, the mirror begins to shift under the influence of light pressure. And since the photons are distributed randomly, sometimes more photons arrive at the mirror during a given time interval, sometimes less, and this light pressure force is also random. So: the quantization of light leads to a random force acting on the mirrors in LIGO. This force causes a random shift of the mirrors, which is recorded at the output of the interferometer as a spurious signal.

Explanation about quantum noise. A random distribution of the number of photons produce a random force of radiation pressure (left). On the other hand, a random distribution of photons in time leads to amplitude fluctuations at the photodetector (right). Both noise depend on wavelength, light power and shoulder length. The noise of radiation pressure is less, the greater the mass of mirrors. Credit: [1].
The noise of radiation pressure is stronger, the greater the power of light incident on the mirrors (i.e., the flux of photons). The signal from the GW also increases with increasing light power in the detector. The shot noise normalized to the signal decreases. As a result, it turns out that you can increase the sensitivity limited by shot noise by increasing the power of light, but you will have to pay for it with increasing noise of radiation pressure. And vice versa. There is no way in the classical way to suppress both quantum noise at once. Will have to use quantum technology.

Dependence of sensitivity on light power: shot noise (blue) decreases, and radiation pressure noise (green) increases proportionally.
2. Compressed light
There is a wonderful article on Habré about squeezed light by qbertych . If you do not know what compressed light is, I highly recommend that you first read his article. I will be brief.
If you look at the light as a wave, the characteristic parameters will not be the photon flux and the delay between them, but the amplitude and phase of the wave. Usually they talk about phase and amplitude quadratures of light.
E=E0 cos( omega0t+ phi)=E0 cos omega0t cos phi−E0 sin omega0t sin phi==Ef sin omega0t+Ea cos omega0t
If the signal of interest to us is contained in the phase of light, and it is small enough, then we can make an approximation:
E=E0 sin phi approxE0 phi; quadEa=E0 cos phi approxE0
Therefore, the value Ef called phase quadrature - it contains information about the phase.
Accordingly, shot noise is a fluctuation of the phase of light, and the noise of radiation pressure is caused by amplitude fluctuations.
Uncertainty in phase and uncertainty in amplitude are related by the Heisenberg relation:
Delta2Ea Delta2Ea leq frac12
In a conventional laser beam, these uncertainties are equal. However, it is possible to compress the phase uncertainty by increasing the amplitude uncertainty - the main thing is that their product satisfies the uncertainty relation. Such light is called squeezed:
Delta2Esqzf=e−2r Delta2Ef, Delta2Esqza=e2r Delta2Ea Delta2Esqzf Delta2Esqza= Delta2Ef Delta2Ea leq frac12,
where r is the compression ratio.
Generally speaking, even in the absence of a powerful beam, vacuum fluctuations always exist. They can also be compressed to obtain a compressed vacuum: on average, the number of photons in it is zero, but the fluctuations of the amplitude and phase are compressed.

It is the vacuum fluctuations entering the detector through the signal port that are the source of quantum noise in LIGO. Therefore, if this vacuum is compressed in phase, this will reduce shot noise in the detector.
This approach has been used in the GEO600 detector for the past 8 years, reducing shot noise by four times, and since this year it has also been implemented in LIGO, reducing shot noise by half (which increases the number of recorded events by 8 times).


Left: An example of improved LIGO sensitivity with squeezed light. Right: the best compression to date was created in our group several years ago: vacuum fluctuations were suppressed by 15 dB.
However, everything is not so simple: according to the uncertainty relation, if we compress the phase, we increase the fluctuations in amplitude. And they increase the noise of radiation pressure. And again you have to choose which noise to reduce by increasing the other. But is it possible to somehow get around this limitation?
3. Frequency dependent compression
Fortunately, two quantum noise limits the sensitivity of the detector at different frequencies: at low noise the radiation pressure is much stronger than shot pressure, and at high - vice versa. Therefore, it is possible to prepare a tricky compression of light, where at low frequencies the light is compressed in amplitude (and therefore the radiation pressure noise decreases), and at high frequencies - in phase (and therefore shot noise is reduced).

Frequency-dependent compression: at different frequencies, the amplitude, phase, or a combination thereof is compressed. As a result, sensitivity is improved at all frequencies. [SSY Chua et al 2014 Class. Quantum Grav. 31 183001]
Fundamentally, the reason for the need for frequency-dependent compression is that the radiation pressure on the mirrors also creates light compression, but in a different quadrature. This can be seen in the image below: if you use conventional compression at the input, at the output it acquires a frequency dependence due to radiation pressure. To "cancel" this frequency dependence, you need to set the inverse dependence for compression at the input.

An example from the article: the dependence of improving the sensitivity of the interferometer when using conventional compression as a function of frequency and different measurement phases is shown above - the signal is in phase quadrature, and it can be seen that if the sensitivity increases at high frequencies (blue color), then at low frequencies it decreases (red ) Using frequency-dependent compression can improve sensitivity at all frequencies.
So, conceptually the problem of reducing quantum noise at all frequencies is solved, the question remains: how to implement such a frequency dependence. To do this, you need to figure out how to turn the compressed phase into a compressed amplitude. Actually, it’s very simple: to produce a phase shift:
Esqzf=E0e−2r sin( phi) rightarrowE0e−2r sin( phi+ pi/2)=Eae−2r
Usually, a simple mirror is enough to phase shift, which will change the length of the path traveled by the light. However, in this case, you need a device that will create a frequency-dependent phase shift: do not shift the phase at high frequencies, but shift at low p i / 2 .
Currently, the leading concept of creating frequency-dependent compression in all designs of future detectors is the use of additional filtering resonators. If the compressed vacuum is reflected from such a resonator when it is detuned from the resonant frequency, it will acquire the necessary frequency dependence. However, it has great difficulty: in order to create the required frequency dependence, the resonators must be several hundred meters long in a vacuum, and this is very expensive and difficult to control. We have another idea.
The fact is that in the detector itself there are already many resonators of suitable sizes, low losses and a well-known control method, but they cannot be used directly - for frequency-dependent compression, it is necessary to detun from resonance. But each resonator has many resonant frequencies, while the detector only works on one of them. The idea is to use a different resonance, reflecting the squeezed light from the interferometer itself to obtain the necessary frequency dependence. The question remains: how to use the frequency dependence created at a frequency different from the main working frequency of the laser. And then quantum entanglement comes to the rescue.
4. Quantum entanglement and the EPR paradox
The question of the nature of entanglement is undoubtedly worthy of a separate article. I discussed a little more intricacy in a previous article on the Habré, so here I will only briefly describe its main properties. Let's start with the EPR paradox (Einstein-Podolsky-Rosen): three gentlemen noticed that there is a catch in quantum mechanics. On the one hand, there is the uncertainty principle, which says that it is impossible to accurately measure the coordinate and momentum of a particle at the same time (and in our case, the amplitude and phase of light). On the other hand, one can make such a simple experiment: take the particle decay event in which two identical particles are born. According to the law of conservation of momentum, they will scatter in opposite directions at the same speed. If we measure the momentum of one particle, we will know exactly the momentum of the second. If we measure the coordinate of the second particle, we will simultaneously know exactly both the coordinate (we measured it) and the momentum (we predicted it from the measurement of the first particle), which, it would seem, is impossible due to the uncertainty relation. The visible paradox is solved by introducing the concept of entanglement of particles: two particles are not independent of each other, they are described by one wave function. This wave function is nonlocal: until the moment of measurement it is impossible to say which of the particles flew in which direction. In a sense, they both flew in both directions at once, and only at the moment of measurement there was a random choice of which particle was measured. Their coordinates and momentum are connected so that the uncertainty relation does not apply to their relative value. Moreover, if one of the particles is acted upon, for example by some force, the second particle will also “feel” this force - its measured parameters will change accordingly.
So, for us the most important thing: if we have two particles, we can accurately predict the properties of the second particle by measuring the first. We can put a source of influence on the path of one particle, and it will act on two at once. Having made the correct measurement, we can see the result of this effect.
How we use it (it was proposed for the first time in an article in Nature Physics [2]). The role of particles in the EPR is played by two beams of compressed vacuum at two frequencies: the fundamental frequency of the interferometer and the frequency of the next resonance of the resonator. We confuse them, one of them (high frequency) is reflected from the tuned resonator and measured. He gets a frequency dependence. Since the rays are entangled, this frequency dependence is also transmitted to the beam at the fundamental frequency. After measurement, we can predict the signals in the main beam ideally with perfect accuracy. To do this, we separately measure on two separate detectors, and optimally process the data.

A complete frequency-dependent compression scheme based on entanglement from [2]. OPA (Optical Parametric Amplifier) creates two entangled beams of compressed vacuum at different frequencies, both of which are sent to the detector. A beam at the carrier frequency resonates in the interferometer. A beam at a high frequency is detuned from one of the higher resonances. At the output, the rays are separated and detected on two different homodyne detectors, after which they are processed in an optimal way.
5. Experiment
Our experiment does not include a full interferometer with moving mirrors. Instead, we are exploring the possibility of obtaining frequency-dependent compression using entangled light reflected from a resonator.

Simplified experimental design. Instead of a full interferometer, we have one 2.5m long optical resonator. Instead of two different homodyne detectors, we use one detector, but two reference beams of different frequencies.
As I wrote above, in an interferometer, radiation pressure creates a frequency dependence of compressed light, which spoils the sensitivity of the detector. In order to cancel this frequency dependence, we need to create an inverse frequency dependence of the squeezed light. In our experiment, the sensitivity spoils not the radiation pressure (we do not have moving mirrors), but the detuning of the detector from resonance (see the picture below (a)). When measured in a signal readout (phase readout), this spoils the sensitivity at low frequencies (red).
To restore sensitivity, we rebuild an additional ray (idler) from resonance in the opposite direction. Then after measurement, we can completely restore sensitivity. In terms of EPR - we can predict the result of measuring the phase quadrature with better accuracy using quantum entangled light.

Two experiments to observe frequency-dependent compression. In the first (a), we built up the signal beam from the resonance of the detector, thereby spoiling the sensitivity in the phase quadrature (and creating a frequency dependence of the squeezed light). In the second, we created an additional frequency dependence for the second ray (idler) and due to quantum entanglement between the two rays, signal and ilder were able to restore the damaged sensitivity by canceling the frequency dependence introduced in the first experiment.
In the image above, the frequency dependence in (a) is rather blurry. This is due to limitations in post-processing: ideally, two separate homodyne detectors are needed, the signals from which can be filtered optimally. However, in another mode, we can obtain a beautiful frequency dependence of the squeezed light if we rebuild both rays from resonance in one direction. Such a scheme is not relevant for the detector, but gives an idea of the installation options. Well, just beautiful experimental data :)

6. Conclusion
To summarize. Quantum fluctuations of light are the main and most fundamental source of noise in all modern and future detectors. To suppress them, one can use quantum correlations - squeezed light. However, in order to reduce noise in the entire frequency range of the detector, it is necessary to compress amplitude fluctuations at low frequencies and phase fluctuations at high frequencies. Such frequency-dependent compression is proposed to be carried out using special filtering resonators. Traditionally, such resonators are very expensive and difficult to implement. Our alternative is to use the detector itself as a filter resonator, using quantum entangled light. We made an experiment and showed that quantum entanglement actually allows to realize this idea.
This approach is not a panacea, alas: you have to pay for convenience. For the concept to work fully, it is necessary to use two homodyne detectors, which is quite difficult experimentally. In addition, the second detector adds noise to the sensitivity - albeit much less than you can gain from compression.
In this work, we played around with intricacies and squeezed light and showed how we can use them to improve the sensitivity of future detectors. But this, of course, is only the first step on a long road to implementing this approach in a real detector: you need to check how everything works with a real interferometer, with moving mirrors, two homodyne, and so on. In general, the work is still full.
For those interested in the details, see our article and the article where the idea was first presented [2].
[1] S. Hild Beyond 2nd Generation GW detectors
[2] Y. Ma et al, Proposal for gravitational-wave detection beyond the standard quantum limit through EPR entanglement, Nature Physics volume 13, pages 776–780 (2017)
7. Miscellaneous
And now some news about LIGO:
- Currently, LIGO have registered 26 events over the last six months of work in the O3 work cycle. Events can be monitored at https://gracedb.ligo.org/superevents/public/O3/ , and for an iPhone there is a whole application .
- The most interesting was perhaps the recent event with the possible detection of the fusion of a black hole and a neutron star. You can read, for example, N + 1 or Scientific American . In general, everything is very interesting.
- Another event with a mass of black holes more than 100 solar. It is believed that the usual mechanisms of the formation of black holes do not allow the formation of BHs of such masses (with masses between 55 and 130 solar). There may be more exotic mechanisms of education, but in any case, curious, read the article here .
- Over the past couple of years, rumors and unhealthy sensations have flared up around LIGO, they say, scientists have not seen any gravitational waves, all these are errors in the calculations. A science team from Denmark has published several articles of varying degrees of revelation. LIGO finally responded with a large and very detailed detector data processing guide . The article itself is not directly a response to Danish articles, but it also parses the mistakes made there. I'm not sure that I will get to a detailed analysis of the article on the Habré, but there are a lot of interesting things there, and it’s not badly written, read it.
And finally: if you want to watch my attempts to figure out how to conduct a scientific twitter, welcome: @hbar_universe .
All Articles