In the world of cryptography, there are many easy ways to encrypt a message. Each of them is good in its own way. One of them will be discussed.

Ylchu Schzzkgow

Or translated from "Caesar's Cipher" into Russian - Caesar's Cipher .

- What is its essence?

- He encodes the message, shifting each letter by N points. Caesar's classic cipher moves letters three steps forward. In simple words - it was “abv”, it became “where”.

“But what about the letters at the end of the alphabet?” What about spaces?

Everything is alright with them. If shifting a letter, the cipher goes beyond the scope of the alphabet - it starts counting all over again. That is, the letters "Eyuya" turn into "abv." And spaces remain spaces.

- Should N necessarily be equal to three?

Not at all. N may differ from the triple. Any N in the range [1: M-1] is allowed, where M is the number of letters in the alphabet.

Such a cipher is easy to decipher if you know about its existence. But it was not his “reliability” that attracted me, but something else.

Tie

One summer day I wanted to know:

• But what if I encrypt a word using Caesar, and I get an existing word at the output?
• How many such words are “shifters”?
• And will there be a pattern if N is changed?

I started looking for answers to these questions in the same minutes.

Task: Find all the words

Retreat. From the concerts of Mikhail Zadornov and personal experience, I understood two things:

1. Americans are not offended by the speech of Russian comedians.
2. The Russian language is strong and powerful. And there are a lot of words in it.

Therefore, I decided to take the English language as my basis. In addition, once upon a time there was infa that the English-speaking guys were able to put together a complete dictionary of English words. What prompted me to find such a dataset.

The first line of sluggish googling brought me to this repository . The author promised 479K English words in convenient formats. I liked the json file in which all the words were laid out in a convenient form for loading into the Python dictionary.

After the first autopsy, it turned out that there were fewer words - 370 101 pieces. “But this does not matter, because for a good example it’ll be enough,” I thought.

words = json.load(open('words_dictionary.json', 'r')) len(words.keys()) >> 370101
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

First you need to create an alphabet. I decided to make it a list in the most convenient way for me. It was also necessary to remember the number of letters in the alphabet:

 abc = list('abcdefghijklmnopqrstuvwxyz') abc_len = len(abc)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

At first it was interesting to make the function of translating a word into encrypted. Here's what happened:

 #   - def cesar(word, abc, abc_len, step=3): word_list = list(word) result = [] for w in word_list: i = abc.index(w) i = (i+step) % abc_len wn = abc[i] result.append(wn) result = ''.join(result) return result
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

I decided to make a big cycle of all the words and start translating them one by one. But came across a problem. It turned out that some words contained a “-” sign, which was surprising and natural at the same time.

Without thinking twice, I counted the number of such words and it turned out that there were only two of them. After which he deleted both, because it will hardly affect the result. To help me, this function was born:

 #   «-»     def rem(words): words_list = list(words.keys()) words = {} for word in words_list: if '-' in word: words_list.remove(word) else: words[word] = 1 return words
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

The dictionary looked like:

 {'a': 1, 'aa': 1, 'aaa': 1, 'aah': 1, ... }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

Therefore, I decided not to be smart and replace the ones with encoded words. To do this, wrote a function:

 #   {'word': 1}  {'word': 'cesar-word'} def cesar_all(words, abc, abc_len, step=3): result = words for w in result: result[w] = cesar(w, abc, abc_len, step=step) return result
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

And, of course, we needed a big cycle that will go through all the words, find the words-shifters and save the result. Here he is:

 #       def check_all(words_cesar, min_len=0): words_keys = words_cesar.keys() words_result = {} for word in words_keys: if words_cesar[word] in words_keys: if len(word) >= min_len: words_result[word] = words_cesar[word] return words_result
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

You may notice that in the parameters of the function is “min_len = 0”. He will be needed in the future. For the peculiarity of this dataset was a "strange" set of words. Such as: "aa", "aah" and similar combinations. They gave the first result - 660 words-shifters.

Therefore, I had to put a limit of five at least five characters, so that the words were pleasing to the eye and similar to existing ones.

 words_result = check_all(words_cesar, min_len=5) words_result >> {'abime': 'delph', 'biabo': 'elder', 'bifer': 'elihu', 'cobra': 'freud', 'colob': 'frore', 'oxime': 'ralph', 'pelta': 'showd', 'primero': 'sulphur', 'teloi': 'whorl', 'xerox': 'ahura'}
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

Yes, ten flip words were found thanks to the algorithm. My favorite combination:

primero [First] → sulphur [Sulfur]. Most other pairs Google translator does not recognize.

At this stage, I partially quenched the thirst for knowledge. But ahead were questions like: “What about the other N?”

And using this function, I found the answer:

 #    N def loop_all(words, abc, abc_len, min_len=5): result = {} for istep in range(1, abc_len): words_rem = rem(words) words_cesar = cesar_all(words_rem, abc, abc_len, step=istep) words_result = check_all(words_cesar, min_len=min_len) result[istep] = words_result print('DONE: {}'.format(istep)) return result
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

The cycle finished in 10-15 seconds. It remains only to see the results. But, as I think it’s more interesting when there is a schedule. And here is the final function, which will show us the result:

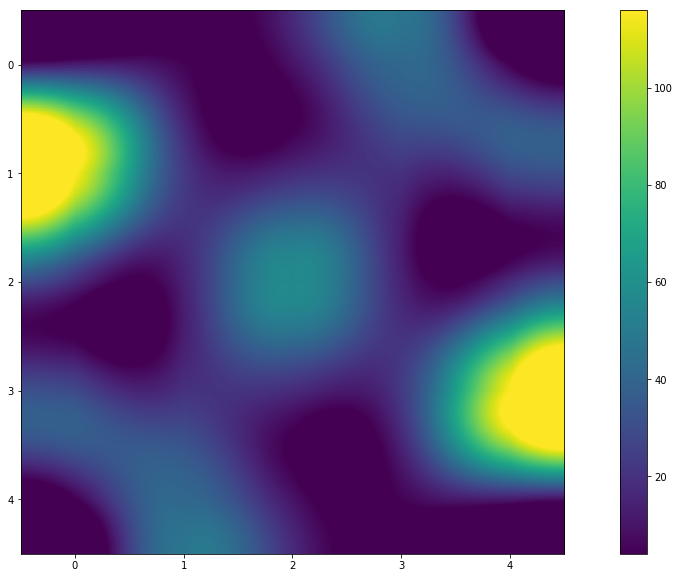
 #   def img_plot(result): lengths = [] for k in result.keys(): l = len(result[k].keys()) lengths.append(l) lengths = np.reshape(lengths, (5,5)) display(lengths) plt.figure(figsize=(20,10)) plt.imshow(lengths, interpolation='sinc') plt.colorbar() plt.show() >> array([[ 12, 5, 10, 41, 4], [116, 23, 18, 20, 29], [ 18, 15, 56, 15, 18], [ 29, 20, 18, 23, 116], [ 4, 41, 10, 5, 12]])
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

Total

Answers to questions at the beginning

“What if I encrypt the word with Caesar, and I get the existing word at the output?”

- This is possible, even very. Some N give much more words than others.

- How many such words “shifters” are there?

- Depends on N, the minimum length and, of course, on the dataset. In my case, with N = 3, the minimum word length of 0 and 5 is the number of words: 660 and 10, respectively.

- And will there be a pattern if you change N?

- Apparently, yes! From the graph (or heat map) you can see that the colors are symmetrical. And the values ​​in the results matrix indicate this. And I will leave the answer to the question “Why so?” To the reader.

Cons of this work

• Not quite correct dataset. Many words are not obvious. Although it may be so. These are “ all ” words of the English language.
• Code is always can be improved.
• “Caesar's code” is a special case of the “Athenian code”, where the formula is:

$$

$$New Letter = A * Past Letter + B$$

For "Caesar's Cipher" A = 1. By the way, he has more nuances, which means more interesting.

My work file with the result and a list of flip words lies in this repository

Efzp zzhgl!