Quantum, or there and back: a new algorithm for studying the quantum-classical transition

Many believe that only quantum physics can be more complicated than classical physics. However, it is much more difficult to study systems that are, so to speak, at the junction of these two worlds. If more and more particles are added to a quantum system, then it will begin to lose its quantum properties and turn into a more classical one. This process is called the quantum-classical transition. Classic computers will not be enough to study such a system, because scientists from the Los Alamos National Laboratory have proposed their own algorithm, which, in conjunction with quantum computers of a couple of hundred qubits, can solve the secrets of the quantum-classical transition. How the algorithm works, why less formulas mean better and what is the practical application of this algorithm? About this and not only we learn from the report of the research group. Go.

Study basis

A quantum-classical transition, if exaggerated, is a decoherence process when a quantum system loses its coherence, that is, acquires classical features. This process can occur for a number of reasons, among which the most obvious is the interaction of the quantum system and the environment. It is also believed that this process is the stone that the process of realizing a quantum computer stumbles upon.



There are many methods to combat decoherence, one is more entertaining than the other, but in total they can be divided into two categories: isolation and implementation. In the first case, scientists are trying to isolate the quantum system from the environment, using very low temperatures and / or high vacuum. In the second case, corrections (code) are introduced into the algorithms of quantum calculations, which will be resistant to errors arising due to decoherence. These methods work, no one denies this, but they are not very scalable. Scientists can keep atoms in a state of superposition for a while if environmental influences are minimized. However, on a larger scale, everything, as a rule, goes to hell.



So, while some brainy people in white coats are looking for ways to deal with decoherence, others are looking for tools to study it. If you want to defeat your enemy, know him by sight, as they say.



Before we plunge into the stream of formulas and explanations regarding the algorithm developed by scientists, it is worth making a short jump in time. Robert Griffiths, an American physicist at Carnegie Mellon University, proposed a theory of sequential histories (events) in 1984: classical physics is close to quantum mechanics, and quantum mathematics can calculate the probabilities of large-scale and subatomic phenomena that relate not to measurement results, but to physical system status. Mr. Griffiths gives as an example photographs of mountains that can be taken from different angles, and then make a picture of a real mountain from them. In the case of quantum physics, it is possible to choose a measurement parameter, but it will not work to combine two measurements to compose a complete picture of a particle before measurement. Prior to the actual process of measuring real position and momentum, it simply does not exist.





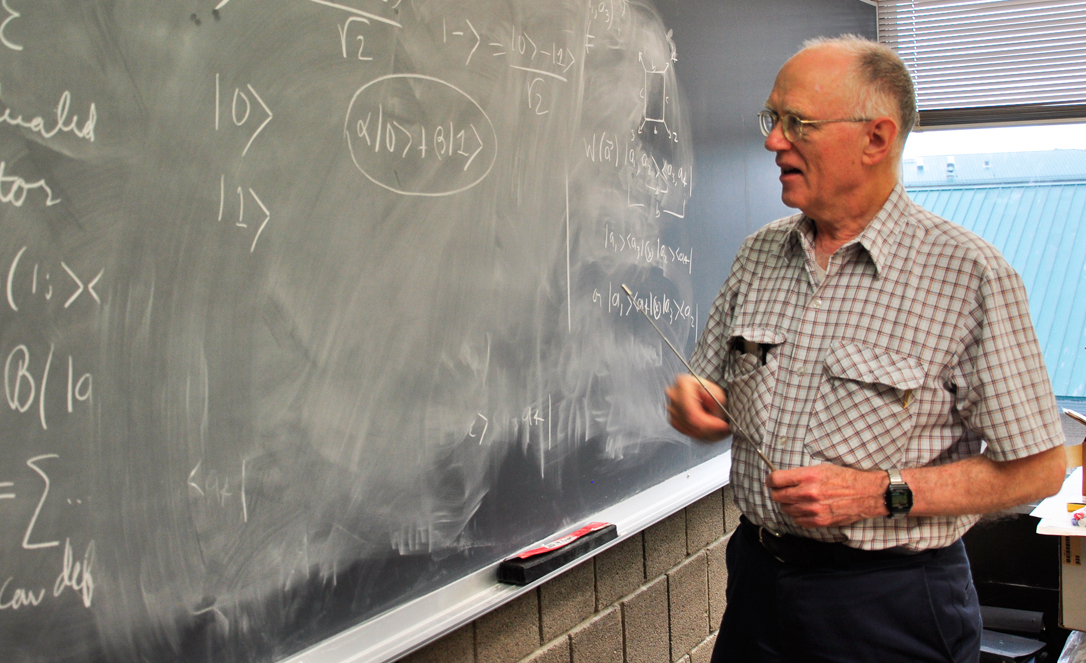
Robert Griffiths



Confused and a little blowing down the roof, but that's not all. In 1989, Murray Gell-Mann and James Hartl, based on the theory of Griffiths, put forward their own. In their opinion, the whole Universe can be considered as a single quantum system without an external environment. If so, then decoherence takes place inside the system, and the result of its activity is quasiclassical domains - sets of sequential histories that are indistinguishable against the background of rough grain due to decoherence.



These theories helped to solve some problems and paradoxes in quantum mechanics, but not all of them. Researchers believe that these conclusions of their predecessors are not widely used due to the fact that the calculations of non-trivial systems (for example, discrete systems of noticeable size or continuous systems that do not allow approximate descriptions by exactly solvable integrals) are extremely complicated. In other words, these theories are good, but only in simple cases.



In recent years, the development of quantum technologies has accelerated greatly, and variational hybrid quantum-classical algorithms ( VHQCA ) have appeared that can cope well with different tasks (factoring, searching for ground states, etc.).



In the work we are considering today, scientists describe their VHQCA algorithm for sequential stories. According to the researchers, their algorithm surpasses classical methods in many parameters, including the size of the systems studied.

Marathon of formulas (theoretical basis)

We already had a historical digression, and now it’s worth a little familiarization with the computational base of the algorithm before considering the results of its work.



The basis of sequential histories (CH) is the history of Y ^α is a sequence of properties in a sequence of time instants t ₁ < t ₂ <... < t _k :







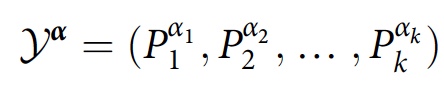
where P α j j is selected from the set of projectors P j that are summed at time t j .



Scientists give an illustrative example: a photon passing through several diffraction gratings and then hitting the screen. In such a situation, the story may be a photon passing through one slit in the first lattice, another slit in the second, etc. Therefore, there is some interference between such stories. And since there are obstacles, it is impossible to classically add up the probabilities of various stories in anticipation of a correct prediction of the point where the photon hits the screen.



The CH framework provides tools for determining when the story family F = { Y ^α } exhibits interference, which is not always obvious. It also defines a class operator:







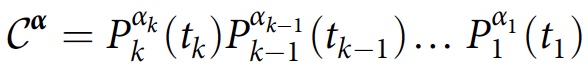
which is a time-ordered product of the projection operators in the history of Y ^α . If the system is initially described by a density matrix ρ, the degree of interference or overlap between the histories Y ^α and Y ^{α ′} will be equal to:







This value is called the decoherence functional. The consistency condition for story family F in this case will look like this:







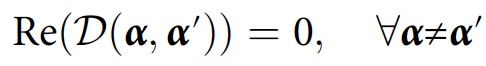
Only if this condition is satisfied, for the history of Y ^{α the} probability will be D ( α , α ). For more simplified calculations, another condition can be applied:







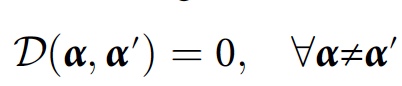
Scientists say that for a numerical algorithm it will be extremely useful to consider approximate consistency while taking into account minor interference:







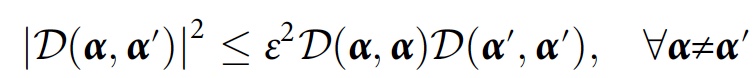
To study the consistency that arises solely from decoherence (i.e., recordings in the environment), the researchers proposed a method that instead takes a partial trace over E , which is a subsystem of the environment:







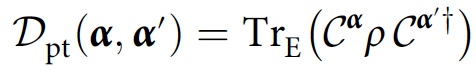
With this modification, the consistency condition will look like this:







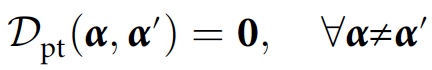
where 0 is the zero matrix. Instead of indicating the absence of environmental interference, consistency indicates the presence / absence of contradictions in the records of stories in the environment.





Image No. 1: a story branching scheme for k time steps.



Given the marathon of formulas and an understanding of sequential stories, scientists point to the evidence of the fact that classical numerical schemes for CH are not able to cope with the task.



The image above shows an example where there are stories of the aggregate of the nth number of particles with 1/2 spin for k time steps. The number of stories is 2 ^nk ; therefore, there are ~ 2 ^{2 nk} functional elements of decoherence. In addition, the evaluation of each functional element of decoherence D ( α , α ' ) requires the equivalent of a Hamiltonian simulation of the system, i.e., multiplication of 2 ⁿ x 2 ⁿ matrices. This means that modern clusters will need hundreds of years to calculate the consistency of a family of stories with k = 2 time steps and n = 10 spins.

VCH Hybrid Algorithm

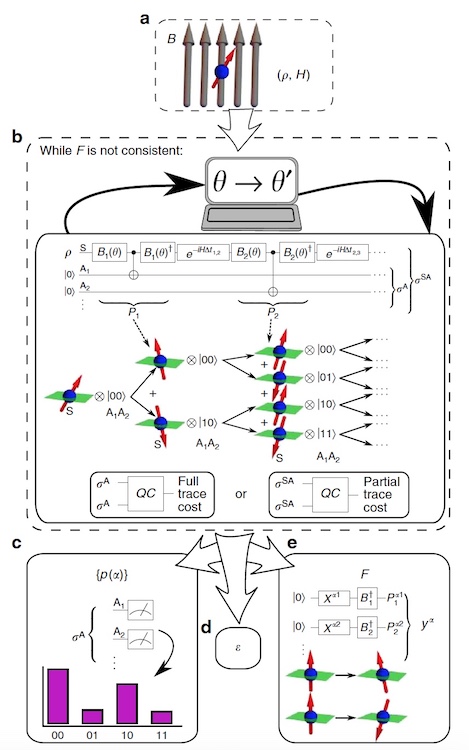
Image # 2: VCH block diagram.



Scientists called their VHQCA algorithm VCH (variable sequential stories). The VCH takes as input the physical model (i.e., the initial state ρ and the Hamiltonian H ) and some ansatz * for the types of projectors that need to be considered.

Ansatz * is a hunch about what the solution of the equation should be and what form it should have.

The following data is available as the resulting data:

• family of stories F , which (approximately) is a complete and / or partial trace in the form of projection operators prepared on a quantum computer;
• probabilities of the most probable stories of Y ^α in F (sorry for the pun);
• estimation of the parameter of consistency ε .

The VCH includes a parameter optimization cycle where a quantum computer evaluates a cost function that quantifies the mismatch of a family, while the classic optimizer adjusts the family (i.e., changes the parameters of the projector) to reduce costs.



To calculate costs, it is necessary to take into account that the elements of the decoherence functional form a positive semidefinite matrix. This property is used in VCH to encode D in the quantum state σ ^A , whose matrix elements are ⟨α | σ ^A | α ′ ⟩ = D ( α , α ′ ).



2b shows a quantum scheme that prepares σ ^A by transforming the initial state ρ ⊗ | 0〉 〈0 | in SA systems (where S models the physical system of interest and A is an auxiliary system) to the state σ ^SA , the limit value of which is σ ^A.



For consistency of the full trace of the matrix, a global measure of consistency is introduced, which quantitatively determines how far σ ^A from the diagonal, which serves as a function of costs:







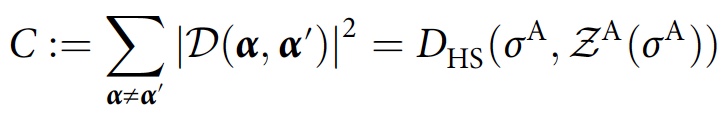
where D _HS is the Hilbert-Schmidt distance and Z ^A ( σ ^A ) is the phase (all off-diagonal elements are set to zero) version of σ ^A.



This quantity tends to zero if and only if F is consistent. For the case of a partial trace, a similar cost function is obtained, but with σ ^A replaced by σ ^SA :







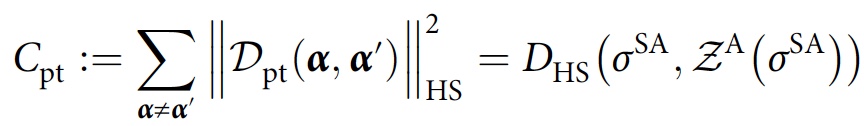
The parameter optimization cycle leads to an approximately consistent family of stories F , where the consistency parameter ε is bounded from above as part of the final costs.



2c shows the generation of probability for the most probable stories by repeatedly preparing σA and measuring on a standard basis, where the measurement frequencies give the probabilities.



2e shows how to prepare a set of projection operators for any given history in F.

Experiment Results

Several different experiments were performed using the VCH algorithm. We will consider two - a spin in a magnetic field and a chiral molecule.

Spin in a magnetic field

Image No. 3



In the first experiment, we considered two time histories of a particle with spin 1/2 in the magnetic field Bz , whose Hamiltonian is H = - γBσ _z . The stories we are considering have a time step Δt between the initial state and the first projector, and also between the first and second projector. In addition, it is worth noting that only projectors on the xy plane of the Bloch sphere are considered.



The image above shows the cost diagram for the ibmqx5 quantum processor, as well as for the simulator, whose accuracy was limited by overlaying the same final statistics that were collected using the quantum processor. Several lows found when running VCH on ibmqx5 overlap the diagram. Since these minima correspond quite well to theoretically consistent families, this represents the success of VCH in practice.

Chiral molecule

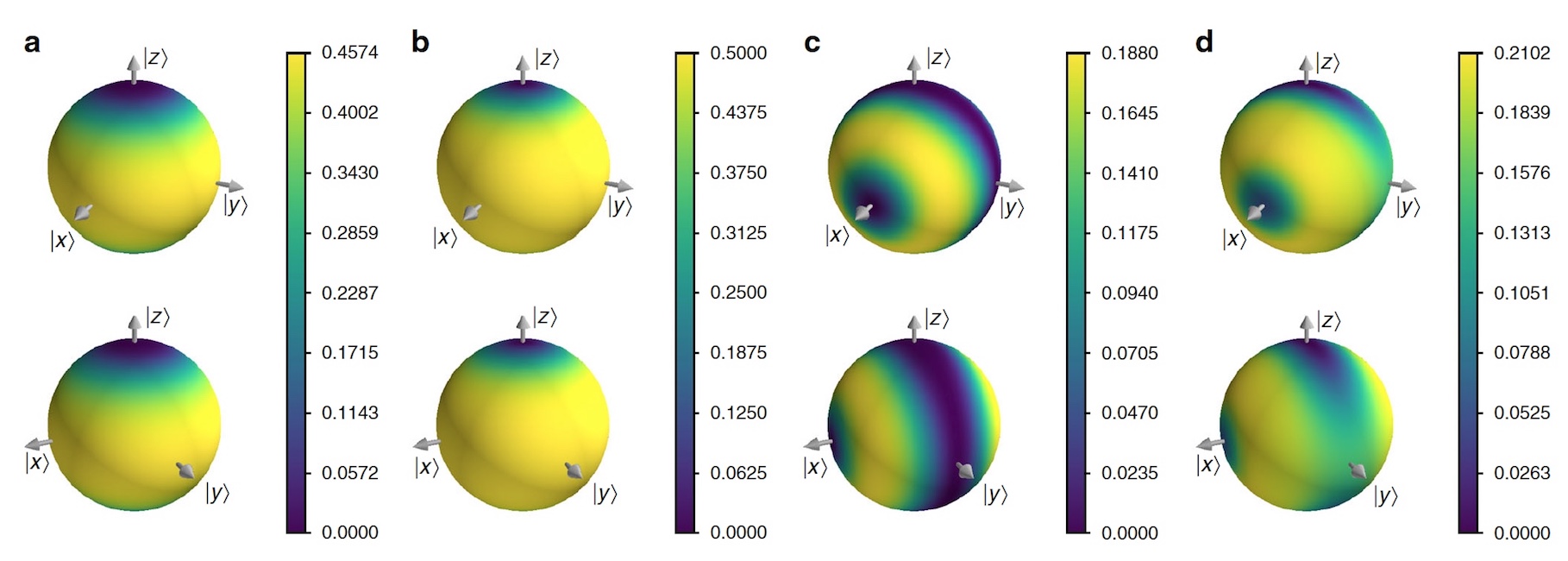
Image No. 4



The chiral molecule was chosen for practical experiments, as this is an excellent way to determine the application of VCH. The chiral molecule was modeled as a two-level system in which the right | R〉 and left | L〉 chirality states are described as | R⟩ / | L⟩ = | +⟩ / | -⟩ = 1 / √2 * (| 0⟩ ± | one⟩).



An isolated chiral molecule tunnels between | R⟩ and | L⟩, but scientists speculate that it is in a gas, where collisions with other molecules transmit information about the chirality of the molecule into its environment. This transmission of information is modeled by rotation through an angle θ _x around the x- axis of a medium qubit controlled by the chirality of the system.



Scientists then consider simple families of stationary stories, where a set of projectors corresponds to the same base all five times (for simplicity of modeling, it was found that the molecule collides with other molecules 5 times). Suppose that θ _z is the angle of precession due to time tunneling between collisions, then it is possible to investigate the competition between decoherence and tunneling. The image above shows the results of this simulation.



Scientists note a curious fact - there is a transition from the quantum regime, where chirality is not sequential, to the classical regime, where chirality is both sequential and stable over time.



For a more detailed acquaintance with the nuances of the study, I recommend that you look into the report of scientists and additional materials to it.

Epilogue

This work demonstrated a new algorithm, which, in conjunction with existing and future quantum computers, can best describe such a complex and confusing process as a quantum-classical transition. The study of this phenomenon is of great importance if we ever want to create a real, working and effective quantum computer, the operation of which will not be affected by decoherence.



VCH algorithm is at the initial stage of development, but already shows its performance. In the future, scientists intend, naturally, to improve it. Be that as it may, the prospects for the early implementation of quantum computing do not just remain at the same level, but grow with each such study.



Thank you for your attention, remain curious and have a good working week, guys! :)



Thank you for staying with us. Do you like our articles? Want to see more interesting materials? Support us by placing an order or recommending it to your friends, a 30% discount for Habr users on a unique analogue of entry-level servers that we invented for you: The whole truth about VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps from $ 20 or how to divide the server? (options are available with RAID1 and RAID10, up to 24 cores and up to 40GB DDR4).



Dell R730xd 2 times cheaper? Only we have 2 x Intel TetraDeca-Core Xeon 2x E5-2697v3 2.6GHz 14C 64GB DDR4 4x960GB SSD 1Gbps 100 TV from $ 199 in the Netherlands! Dell R420 - 2x E5-2430 2.2Ghz 6C 128GB DDR3 2x960GB SSD 1Gbps 100TB - from $ 99! Read about How to Build Infrastructure Bldg. class c using Dell R730xd E5-2650 v4 servers costing 9,000 euros for a penny?