The book “Thin physics. Mass, ether and unification of world forces "

Hello! Finally, the book by Frank Wilczek came to us from the printing house, the last time we did a review here. Now we share the passage "Symmetry: Differences without Differences."



The main idea of ​​quantum chromodynamics is symmetry. “Symmetry” is a common word, and its meaning, like the meaning of other similar words, is not completely unambiguous. Symmetry can mean balance, nice proportions, regularity. In mathematics and physics, the meaning of this word is consistent with all of these ideas, but is clearer.



I like the definition that symmetry means that you have a difference without distinction. Lawyers also use the phrase “difference without difference”. In this context, it usually means the expression of the same, but in other words. Here is an example from comedian Alan King: “My lawyer warned me that if I died without expressing my last will, then I would die without leaving a will.”



To understand the mathematical concept of symmetry, consider an example. We can build a cute little tower of examples containing the most important ideas in an easily digestible form, in the world of triangles (Fig. 7.1).











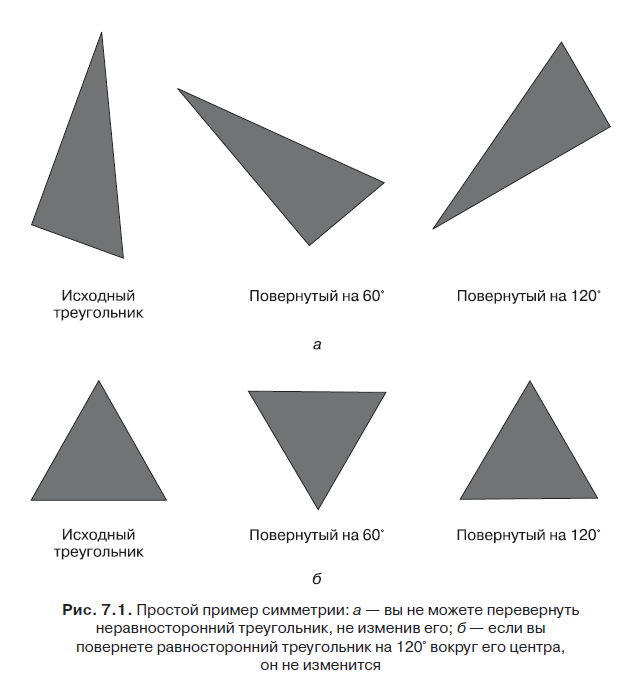
You cannot flip most triangles without changing them (see Figure 7.1, a). However, equilateral triangles are special. You can rotate an equilateral triangle by 120 or 240 ° (that is, twice), while obtaining the same shape (see Fig. 7.1, b). An equilateral triangle has non-trivial symmetry, since it allows for differences (between the triangle and its rotated versions), which, after all, do not create any differences (rotated variants have the same shape). Conversely, if someone tells you that the triangle looks the same, being rotated 120 °, you can conclude that this triangle is equilateral (or that the person is lying).



The next level of complexity is manifested when we consider a set of triangles with different types of sides (Fig. 7.2). Of course, if we rotate one of them by 120 °, we will not get the same triangle - the sides will not be the same. In fig. 7.2. The first triangle (RBG) turns, turning into the second triangle (BGR), the second turns, turning into the third (GRB), and the third turns, turning into the first. However, the complete set containing all three triangles does not change.



On the other hand, if someone tells you that a triangle with three different kinds of sides, along with some other things, still looks after turning 120 °, you can conclude that the triangle is equilateral, and that there are two equilateral triangles with different positions of the sides (or that a person is lying).



Let's add the last layer of complexity. Instead of triangles with sides of different colors, consider the laws associated with these triangles. For example, a simple law may be that when a triangle is compressed, it neatly folds so that its sides are bent. Now suppose that we only investigated RBG triangles, so we really derived the compression law only for these triangles. If we know that rotation by 120 ° provides a difference without differences, that is, a rotation by 120 ° determines symmetry in a mathematical sense, then we can conclude not only about the existence of other types of triangles, but also that they also neatly collapse when compressed .









This series of examples on simple forms demonstrates the power of symmetry. If we know that an object has symmetry, we can conclude about some of its properties. If we know that a set of objects has symmetry, then on the basis of knowledge of one object we can conclude about the existence and properties of others. And if we know that the laws of nature have symmetry, then on the basis of knowledge about a single object, we can conclude about the existence, properties and behavior of new objects.



In modern physics, symmetry allows one to predict the existence of new forms of matter and to formulate new, more comprehensive laws. For example, the special theory of relativity can be considered as a postulate of symmetry. It tells us that the equations of physics should look the same if we transform all the objects in these equations, adding a constant value to their velocities. This value transfers one world to another, moving relative to it at a constant speed. Special theory of relativity says that this difference does not make a difference - the behavior in both worlds is described by the same equations.



Although the details are more complex, the procedures for using symmetry to understand our world largely correspond to those we used in our simple example from the world of triangles. We believe that our equations can be transformed in such a way that they change in principle, and after that we demand that they not actually change. The possible difference is irrelevant. As with the triangle examples, several rules must be followed to ensure overall symmetry. Objects that are present in the equations must have special properties, form connected sets and obey closely related laws.



Thus, symmetry can be a powerful idea with rich consequences. In addition, this idea is very fond of nature. Get ready for a public demonstration of love.



»More information about the book can be found on the publisher's website.

» Table of Contents

» Excerpt



For readers of this blog 20% ​​discount coupon - Wilczek