それで、 Progopediaプロジェクトの一環として過去6か月間に書いたものからフィボナッチ数を計算する10の最も不自然な方法の評価。 問題を明確にするために、プログラムの出力は次の形式の最初の16の数字である必要があります。
1、1、2、3、5、8、13、21、34、55、89、144、233、377、610、987、...
10. サンスクリプト
言語のすべての要素がフロー図と呼ばれる実際の「コード」がコンパイルされる基本ブロックの形式で提示される視覚プログラミング言語。 この言語は、図のサイズ(2つ、まあ、30個の要素-ブロック間のリンクのスクロールや最終的な混乱なしに1つの図で使用できる最大要素)とキー言語構造を使用する不便さ(各サイクルまたは条件付き遷移には独自の説明が必要です)によってランキングの場所を獲得しましたマルチレベルのネスティングとループパラメータの形式でのグローバル変数の転送により、プログラムロジックを即座に混乱させる1つ以上の個別のダイアグラム)。 まあ、実際には視覚によって-プログラムは書かれておらず、描かれており、キーボードは定数値を入力し、(オプションで)基本ブロックの名前を変更してコメントを書くためにのみ使用されます。

マスターフローチャート

サイクル本体
9. gnuplot
この言語の機能(バージョン4.4.0まで)は、サイクル自体が存在しないことです。 しかし、これは許されます-結局、gnuplotは汎用言語ではなく、グラフ作成プログラムです。 サイクルをシミュレートするには、サイクルの本文を含む個別の解釈済みファイルを作成します。このファイルは、サイクルを開始するために「読み取り」され、反復ごとに「再読み取り」されます。
Run.gpファイル(メイン)
#!/usr/bin/env gnuplot
i = 1
a = 1
b = 1
res = ''
load "fibonacci.gp"
print res, '...'
Fibonacci.gpファイル(ループシミュレーション)
res = res . a . ', '
c = a
a = b
b = b+c
i = i+1
if (i <= 16) reread
8.ハスケル
最も有名なHaskellチップの1つである無限リストを備えた遅延計算により、1行のコードでフィボナッチ数を決定できます(計算はできません)。残りのコードは必要な数を要求し、正しい形式で表示します。 それにもかかわらず、手続き型パラダイムの枠組みで古典的な教育を受けたプログラマーにとって、この方法は明白とはほど遠いものであり、確かに自然ではありません。
module Main where
import Text.Printf
fibs :: [Int]
fibs = 0 : 1 : zipWith (+) fibs (tail fibs)
line n = printf "%d, " $ fibs !! n
main = do
sequence_ $ map line [1..16]
putStrLn "..."
7. SQL
もちろん、SQL自体はプログラミング言語ではありません。ほとんどの実装では、手続き型拡張機能がSQLにアタッチされており、これを使用してタスクが完全に古典的な方法で解決されます。 興味深いのは、純粋なSQLでの拡張のないソリューションです。 ただし、「純粋な」SQLで決定することはできません。標準によれば、クエリ言語にはループとして使用できるものは含まれていません。 決定は、特定の実装とそれに付随する利点に依存して行われます。
7.1。 Oracle SQL(バージョン9i以降)
数値のインデックス(1から16)は、擬似列レベルとconnect by構造を使用して内部クエリで生成されます。 次のクエリでは、フィボナッチ数自体は、Binet式を使用したインデックスによって計算されます。 残りの2つのクエリは、インデックスで番号をソートし、それらを目的の形式の1行に結合します。
SELECT REPLACE(MAX(SYS_CONNECT_BY_PATH(fib||', ', '/')),'/','')||'...' FROM ( SELECT n, fib, ROW_NUMBER() OVER (ORDER BY n) r FROM (select n, round((power((1+sqrt(5))*0.5, n) -power((1-sqrt(5))*0.5, n))/sqrt(5)) fib from (select level n from dual connect by level <= 16) t1) t2 ) START WITH r=1 CONNECT BY PRIOR r = r-1;
7.2。 Oracle SQL(バージョン10g以降)
便利ですが、めったに使用されないため、あまり知られていないモデル演算子を使用すると、SQLクエリ内にループを実装できます。
select max(s) || ', ...' from (select s from dual model return all rows dimension by ( 0 d ) measures ( cast(' ' as varchar2(200)) s, 0 f) rules iterate (16) ( f[iteration_number] = decode(iteration_number, 0, 1, 1, 1, f[iteration_number-1] + f[iteration_number-2]), s[iteration_number] = decode(iteration_number, 0, to_char(f[iteration_number]), s[iteration_number-1] || ', ' || to_char(f[iteration_number])) ) );
7.3。 MySQL
ループでクエリ結果を計算する機能は、Oracleよりも簡潔に実装されています。
select concat(group_concat(f separator ', '), ', ...') from (select @f := @i + @j as f, @i := @j, @j := @f from information_schema.tables, (select @i := 1, @j := 0) sel1 limit 16) t
7.4。 Microsoft SQL Server(バージョン2005以降)
もう1つのかなり簡潔なループ実装、今回は再帰クエリを使用します。
with fibonacci(a, b) as ( select 1, 1 union all select b, a+b from fibonacci where b < 1000 ) SELECT cast(a as varchar)+', ' AS [text()] FROM fibonacci FOR XML PATH ('')
6. FP
FPは、機能のレベル(機能レベル、機能と混同しない、つまり単に機能 )でプログラミングパラダイムを使用するすべての既存のプログラミング言語のプロトタイプです。 1977年に発明され、実際のプログラミング言語というよりは数学モデルです。実装は言うまでもなく、公式の標準さえありませんでした(記述されている唯一の記事を除く)。 それにもかかわらず、私たちの時代には、通常は学生の仕事の一部として書かれたこの言語の通訳がいます。 それらの1つはFurry Pawsであり、その居心地の良い名前は、その使用の「快適さ」にまったく対応していません。
機能レベルでのプログラミングには、基本機能からプログラムを構築することが含まれます。基本機能は、機能(機能形式)を使用して組み合わせることができます。 したがって、〜1は常に1を返す基本関数です。 idは渡された値を返す関数です。[]は引数をシーケンスに結合する関数形式などです。
one = eq.[id, ~1]
dec = sub.[id, ~1]
seq = one -> [~1] ; cat.[seq.dec, [id]]
fibonacci = lt.[id, ~3] -> ~1 ; add.[fibonacci.sub.[id, ~1], fibonacci.sub.[id, ~2]]
main = show.(return @fibonacci.(seq.~16))
5. J
「関数レベルのプログラミング」を使用する別の言語は、FPに続く価値のあるものです。 興味深いのは、ほとんどすべての表現が、ほぼ伝統的なものから完全に不自然なものまで(この記事で必要だったように)いくつかの方法で書けることです。 したがって、たとえば、Binet式を使用したフィボナッチ数の計算は、非常に非公式に記述できます。
load 'printf'
g =: 0.5 * (1 + 5 ^ 0.5)
fib =: (0.2 ^ 0.5) * (g &^ - (1-g) &^)
fstr=: '...' ,~ ,~^:4 '%d, '
fstr printf fib 1+i.16
そして、ほとんどすべての数学演算をJに固有の同等の演算に置き換えることができます。
load 'printf'
g =: -: >: %:5
fib =: (%:5) %~ g&^ - (1-g)&^
fstr =: '...' ,~ ,~^:4 '%d, '
fstr printf fib"0 >:i.16
そして、それは誰にもほとんど明らかではありません%:-平方根の抽出です、>:-増分、-:-2による除算、および%〜-除算、および記録時に配当と除数が交換されます。
再帰を使用した計算:
load 'printf'
fibr=: 1:`(-&2 + &fibr -&1) @.(2&<)"0
fstr=: '...' ,~ ,~^:4 '%d, '
fstr printf fibr 1+i.16
4. ハノイラブ
あまり知られていない難解な言語。そのミニマリズムとメモリのスタックモデルの使用が興味深い。 次の言語とは異なり、主な困難は算術演算の実行ではなく、各ステップで必要なスタック要素の内容を正確に取得することにあります。 ただし、印刷も不快であるため、最初の6つの数値のみが計算されて表示されます。
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;.'...;;;;;;;;;;;;.'...,..''''''..`.'.
..;.'.,.'...:...,.'..;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
"'.,.'...,"'.'...,"''.,...'.,..'..,...'...;.'.,.,!...,,,...;;"'"'"'
言語の説明とコードに関するコメントは、 Hanoi Loveページにあります。
3. ブレインファック
難解なプログラミングのジャンルの古典はBrainfuckです。 コピーや追加でさえ基本操作ではない言語、印刷
3桁の数字は別の歌の価値があり、特定の問題を解決するためにそれを使用するのはマゾヒストの夢です:-)
MullerのBrainfuckでは、メモリセルの内容はバイト変数に格納され、14から16までのフィボナッチ数はメモリオーバーフローを引き起こします。 Brainfuckでの長い演算の実装はもはや症状ではありませんが、実際には診断であるため、ソリューションを記述するとき、メモリセルは1000までの数値を格納できると想定されていました(言語の多くの実装では、かなり大きなデータ型が格納に使用されます)。
++++++++++++++++++++++++++++++++++++++++++++>++++++++++++++++++++++++
++++++++>++++++++++++++++>>+<<[>>>>++++++++++<<[->+>-[>+>>]>[+[-<+>]>
+>>]<<<<<<]>[<+>-]>[-]>>>++++++++++<[->-[>+>>]>[+[-<+>]>+>>]<<<<<]>[-
]>>[++++++++++++++++++++++++++++++++++++++++++++++++.[-]]<[++++++++++
++++++++++++++++++++++++++++++++++++++.[-]]<<<+++++++++++++++++++++++
+++++++++++++++++++++++++.[-]<<<<<<<.>.>>[>>+<<-]>[>+<<+>-]>[<+>-]<<<
-]<<++...
言語の説明とコードに関するコメントは、 Brainfuckページにあります。
2. Brainloller
Lode Vandevenneによって発明されたBrainfuckの最もシンプルなグラフィック方言。
プログラムはPNG画像から読み込まれ、コマンドは異なる色のピクセルで書き込まれ、さらに2つがBrainfuckで利用可能な8つのコマンドに追加されます-現在のピクセルへのポインターを制御します。 Brainfuckのすべての魅力に、「コード」の完全な読み取り不能性と完全な不可能性が追加されています。
補助手段なしの「エンコード」(たとえば、プログラムと画像のコンバーター)。
作者の言語の通訳者は忘却に沈んでしまったので、「プログラム」を生成するために自分で自分で書く必要がありました。 「プログラム」は10倍の倍率で表示されます。
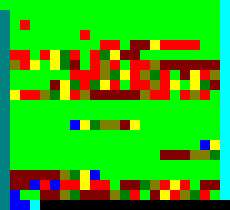
1. 単項
どれほど悪いですか? -読者は震える手で画面をめくって考えます。 はい、悪化します。 以前の言語では、少なくとも多くのプログラムを把握できました。
評価の勝者-単項をご覧ください。 同じLode Vandevenneによって発明されたBrainfuck方言(ああ、Monsieurは倒錯について多くを知っています!)、Brainfuckコマンドがバイナリコードに変換され、単一のバイナリ番号に連結され、その単項レコードが単項プログラムであると仮定します。 フィボナッチ数生成プログラムは、
167967665105731198557055496639385943332278803897935697536099438828197
665241403160165880863622431582784595268769268183940269756210147305655
704025762911607244068691728105306566342622386432823429136972542304655
647901781271798433263001837026612851345264031562174039657802748245705
398528237993320520942720239597540583536934220029626573406470088757427
393143000966310611249037587993216365993804186165097620168960460854977
571944373603975793034586829061577464233522714007498991416860375267535
193648636795096472789203729505034887001634966681420589637468649908257
407260923590831776308356684326657774592110098643361324426156431864437
942781495979555960608253552679248495326880775320385281559763269974848
026839024530519989287202261977272377723622502479809174132505837648641
033569945906182518892142219706483917757108086522763280388915772444727
238483811923456440363260610571471034139736312976255142288379411989404
9017738035(つまり、約1.68 * 10 ^ 906)ゼロ。
ここにリストされている言語は、プログラマが遭遇する可能性のある最悪のものとはほど遠いものと確信しています(いずれにしても、すべてではありません:-))。しかし、私は魔法使いではありません。