Lシステム。 ツリーモデリング

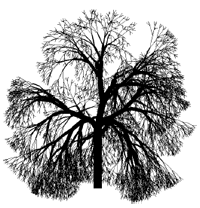
投稿は、Przemyslaw PruschinkiewiczとAristid Lindenmeyer（The Algorithmic Beauty of Plants、Aristid Lindenmayer、Przemyslaw Prusinkiewicz）による本 「Algorithmic Beauty of Plants」の第2章の無料翻訳です。インスピレーションのために:)

最初のモデル。

ツリー分岐プロセスのコンピューターモデリングには、比較的長い歴史があります。 ウラムが提案した最初のモデルは、フォンノイマンが開発したセルオートマトンの概念に基づいていました。 分岐プロセスは反復によって実行され、三角形グリッド上の1つの染色されたセルから始まり、その後、前の反復で染色された細胞の1つだけの頂点に触れた細胞が染色されました。



さらに、このアイデアが開発されました。 マインハルトは、三角形のグリッドを正方形のグリッドに置き換え、結果のセル空間を使用して、ネットワーク構造の形成の生物学的仮説をテストしました。 きれいな分岐プロセスに加えて、彼のモデルは、例えば葉や静脈の間で発生する可能性のある再接続または吻合の影響を考慮しました。 グリーンは、環境を考慮した3次元のセルオートマトンを書き直し、成長プロセスをシミュレートしました。 たとえば、図2.1は家の上のブドウの木の成長を示しています。 Cohenのモデルは、成長のルールで「フィールド密度」の概念を考慮に入れました。これは、たとえば、個別のセルを操作するよりも優れていることが判明しました。





図2.1。 調和のとれたグリーン建築。



これらのアプローチの共通の特徴は、構造の異なる要素と環境との構造の両方の間の相互作用に重点を置いていることです。 そして、この相互作用は明らかに実際の植物の成長に影響を与えますが、そのモデリングは非常に難しい作業です。 したがって、ブランチ間の衝突などの基本的なことすら無視する単純なモデルは、今日ではより一般的です。

ホンダモデル。

ホンダは単純なカテゴリーの最初のモデルを提案し、次のことを仮定しました。

• ツリーセグメントは直線であり、その断面積は考慮されません。
• 反復中に、親セグメントは2つの子会社を生産します。
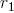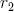• 2つの娘セグメントの長さは、 そして 回;
• 親セグメントとその2つの子会社は同じブランチプレーンにあります。 子セグメントは、 分岐角度で母体を出る 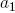そして ;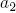
• 重力の作用に関連して、分岐面は「水平面に最も近い」、つまり、母セグメントに垂直で分岐面にある線は水平です。 メイントランクに接続されているブランチについては例外が作成されます。 この場合、一定の発散角が使用されます。 。

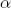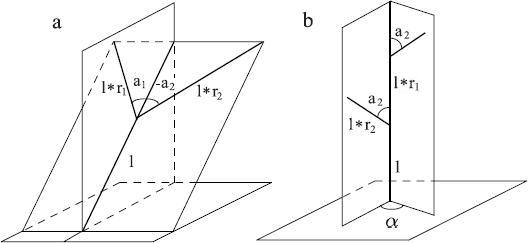
図2.2。 ホンダによると、木の形状。



数値パラメーターを変えることにより、ホンダは多種多様な樹木のような形を受け取りました。 いくつかの改善により、彼のモデルは実際のツリーの分岐プロセスの研究に適用されました。 その後、別の枝の平面が互いに垂直であるツリー構造もカバーするために、枝角に対して異なるルールが提案されました。 ホンダの結果は、エオノとクナイが提案したモデルの基礎となりました。 彼らはいくつかの改善を提案しましたが、その中で最も重要なのは、風と重力を考慮に入れて、太陽​​に対する枝の傾向に対応する特定の方向へのセグメントの回転でした。 同様の概念がCohenによって提案されましたが、RefaiとArmstrongは枝を曲げるためのより物理的に正確な方法を開発しました。



Honda、Eono、およびKuniaiモデルは、一定または可変幅の直線を使用して「木製スケルトン」を構築しました。 合成モデルのフォトリアリズムの大幅な改善は、BlumenfelとOppenheimerによって達成されました。BlumenfelとOppenheimerは、曲がった枝を提示し、枝ノード周辺の表面を慎重にモデル化し、樹皮と葉にテクスチャを適用しました（図2.3）





図2.3。 Blumenfel、Acerグラフィック。



ホンダの研究では、分岐構造は決定論的アルゴリズムに従って構築されました。 対照的に、ReevesとBlau、de Refai、Remfrey、Neil、およびStevesによって提案されたモデルのグループでは、確率的法則が使用されました。 これらのモデルの構築方法は異なりますが、樹木の構造、特に枝を形成する可能性の計算を記述するという一般的なパラダイムを共有しています。 ReevesとBlauは、シミュレートされた構造の生物学的詳細を掘り下げないように努めました（図2.4）。 それどころか、de Refayは確率論的なアプローチを使用して現実的な植物を作成し、個々の時点での芽の活動をシミュレートしました。 タイマー信号を受信すると、腎臓は次のいずれかを実行できます。

• 何もしない
• 花になる;
• 新しい頂点と幹の1つ以上の側枝で終わる幹のセグメントになります。
• 死ぬか消えます。

これらのイベントは、植物種ごとに個別に説明されている確率的法則に従って発生しました。 ステムセグメントの長さと直径、分岐角度などの幾何学的パラメーターも、確率的アルゴリズムに従って計算されました。





図2.4。 森林の写真、リーブス、©1984 Pixar。





図2.5。 油ヤシの天蓋、CIRAD Modelisation Laboratory。



この方法で基本的なタイプの開発法を使用して、Helle、Aldemen、およびTomlinsonは23種類のツリーアーキテクチャを確立しました。 選択した植物タイプの詳細なモデルが開発され、文献に記載されています。 単純なツリーモデルを図2.5に示します。 RemfreyのアプローチはDe Refaiのアプローチに似ていましたが、前者はより長い時間間隔を使用しました。 信頼できる結果を達成するために、確率モデルはその年の間に起こりうる横の芽の行動を記述する必要があることが判明しました。



Lシステムを使用してツリーを生成することは、最初にEonoとKuniaiによって検討されました。 そもそも、Lの正式な定義に基づいて、彼らは高等植物のモデリングには不適切であることを証明しました。 しかし、この証明は、文字列の亀の解釈を持つパラメトリックLシステムには適用されませんでした。 たとえば、図2.6のLシステムは、分岐角の1つがゼロであり、柔軟な一脚構造であり、明確に定義された主軸と横軸を持つホンダモデルを実装しています。





図2.6。 Lシステムからのホンダの一脚分岐ツリーモデル。

n = 10

#define r1 0.9 /* */

#define r2 0.6 /* */

#define a0 45 /* */

#define a2 45 /* */

#define d 137.5 /* */

#define wr 0.707 /* */

ω : A(1,10)

p1: A(l,w) : *→ !(w)F(l)[&(a0)B(l*r2,w*wr)]/(d)A(l*r1,w*wr)

p2: B(l,w) : *→ !(w)F(l)[-(a2)$C(l*r2,w*wr)]C(l*r1,w*wr)

p3: C(l,w) : *→ !(w)F(l)[+(a2)$B(l*r2,w*wr)]B(l*r1,w*wr)



* This source code was highlighted with Source Code Highlighter .

表2.1。 図2.6の一脚木構造の定数。

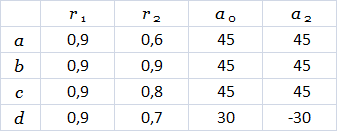
ご注意 あたり -ここで興味深いのは、ツリーノード間のセグメントの太さが一定である必要があることです。また、写真は、幹の太さが最初の枝の前でさえ減少し始めていることを示しています。 他の写真では、これは見られません:)

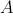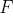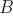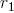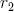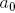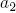表現によると 主軸の上部からの各反復で 幹セグメント そしてサイドアペックス 。 定数 そして 直線セグメントと側面セグメントの長さの減少を示し、 そして -枝角と 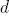-発散角。 モジュール 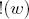線幅を設定します したがって、式 の親からの子セグメントの幅を縮小します 回。 この定数はレオナルドダヴィンチの仮定を満たします。これによれば、水平面のあるツリーのセクションで折りたたまれたすべての枝の総厚は、その下の幹の厚さに等しくなります。 直径のある母枝の場合 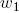同じ直径の2人の娘が出てきます 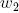、この仮定は方程式を与えます 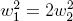したがって、値 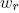等しい 。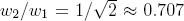

ご注意 あたり -おそらく枝の厚さと幹の厚さによって、それらの断面積を理解する必要があり、最後の方程式で正方形がどこに現れたかが明らかになります。

表現 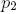そして 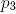側枝のさらなる発展について説明します。 各反復で、まっすぐな頂点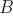（ または ）ある角度で次の次の横頂点を生成します 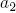または 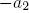母体軸に関連して。 両方の式を使用して、左右の頂点を交互に作成します。 記号 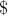カメを自身の軸の周りに回転させ、ベクトル 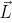カメの「左」の方向は水平に描かれます。 その結果、分岐面は、ホンダのモデルで要求されるように「水平面に最も近い」です。 ベクター形式で書く、 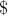以下に従って空間内のカメの向きを変更します：









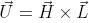
ベクトル 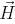、 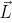そして -亀に取り付けられたメイン、左、および上ベクトル、 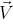-重力の方向と反対方向に向けられたベクトル。 図2.6は、表2.1にリストされている定数でモデル化され、Hondaツリーモデルに一致するツリーを示しています。

対称分岐。

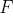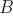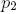図2.7に示す他のLシステムは、両方の娘セグメントが親とゼロ以外の角度を形成するシンポジアル構造をカバーしています。 この場合、トランクの形成によりメインピークのアクティビティが減少します。 サイド頂点のペア （式 ） 式によってさらに分岐が行われます 。 図2.7の単純な構造は、表2.2にリストされている定数を使用して取得され、EonoとKuniaiによって提示されたモデルに対応しています。







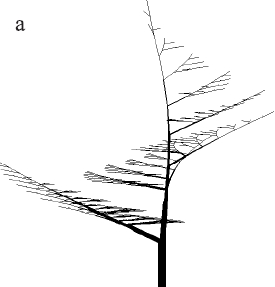
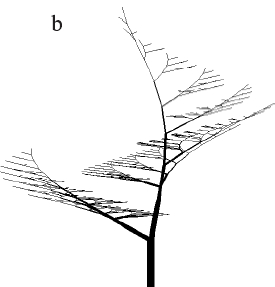
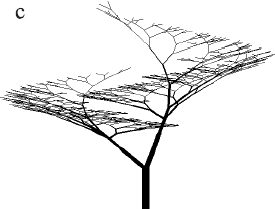
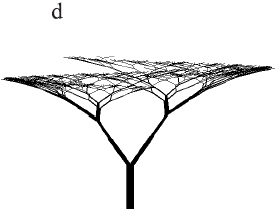
図2.7。 Lシステムで得られた交尾枝EonoとKuniayを持つ木のモデル。

n = 10

#define r1 0.9 /* 1 */

#define r2 0.7 /* 2 */

#define a1 10 /* 1 */

#define a2 60 /* 2 */

#define wr 0.707 /* */

ω : A(1,10)

p1 : A(l,w) : *→ !(w)F(l)[&(a1)B(l*r1,w*wr)]

/(180)[&(a2)B(l*r2,w*wr)]

p2 : B(l,w) : *→ !(w)F(l)[+(a1)$B(l*r1,w*wr)]

[-(a2)$B(l*r2,w*wr)]



* This source code was highlighted with Source Code Highlighter .

表2.2図2.7のシンポディアル分岐を持つツリーの定数。





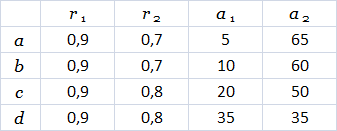
各セグメントの最終的な長さは作成されても設定されており、それ以降の反復では変化しないため、以前のモデルはやや人工的です。 ただし、成長プロセス自体をシミュレートすること、つまり、子会社の成長に伴い親セグメントの長さと幅を増やすことは可能です。 このパラダイムを使用して構築されたLシステムの例を図2.8に示します。

三項分岐。

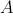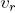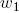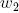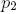ツリーの一般的な構造は、式によって定義されます 。 各反復で、頂点 独自の頂点で終わる3つの新しいブランチを生成します。 パラメータ そして定数 母枝の幅の比率を決定する 子ブランチの幅 。 ダ・ヴィンチの仮定によると かくして 。 表現 そして 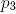枝の長さの漸進的な変化とその直径の増加について説明します。







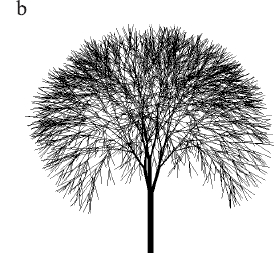
図2.8 三分枝のある木のモデル。

#define d1 94.74 /* 1 */

#define d2 132.63 /* 2 */

#define a 18.95 /* */

#define lr 1.109 /* */

#define vr 1.732 /* */



ω : !(1)F(200)/(45)A

p1 : A : *→ !(vr)F(50)[&(a)F(50)A]/(d1)

[&(a)F(50)A]/(d2)[&(a)F(50)A]

p2 : F(l) : *→ F(l*lr)

p3 : !(w) : *→ !(w*vr)



* This source code was highlighted with Source Code Highlighter .

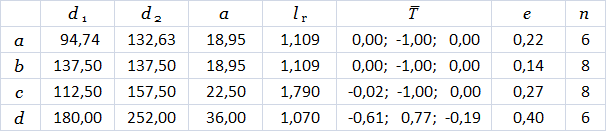
表2.3。 図2.8のツリーモデルの定数。





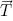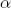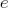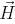
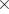
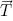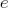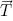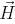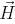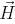
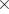
屈性は、この効果によって決定される方向への成長による外部効果に対する生物、たとえば植物の反応です。 特に、光に対する植物の欲求は、曲がった枝の形で現れます。 これは、各セグメントを向性ベクトルで定義された方向に描画した後、カメの小さな回転によってモデル化されます （図2.9）。 回転角aは、式を使用して計算されます = | |どこ -感度、回転に対する軸の感受性を特徴付けるパラメーター。 この式には物理的な説明があります：if ベクトルの終わりに適用される力として解釈する 、そして 開始点を中心に回転できる場合、トルクは 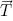。 図2.8のツリーモデルの生成に関連するパラメータを表2.3に示します。 図2.8dのツリーのリアルなレンダリングを図2.10に示します。





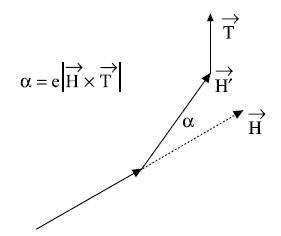
図2.9 訂正 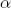セグメント 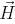向性のおかげで 。





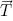図2.10 魅惑的なマスグレイブなどの湖。





図2.11 シュールなリフト。

おわりに

上記の例は、ホンダの木のモデルだけでなく、彼のフォロワーであるEonoとKuniaiのモデルがLシステムを使用して取得できることを示しています。 Shebellはまた、Lシステムが生物学的に正確なツリーモデリングとフォトリアリスティックな画像の合成のためのツールとして重要な役割を果たすことを示しました。 ただし、取得したモデルは一般的な性質のものですが、特定のツリーの構造はまだ開発中です。 Lシステムは、次の章で説明する草本の現実的なモデリングの分野でも広く使用されています。

---

PS 1990年の本の「写実的な」画像が配信されない場合、 algorithmicbotany.orgの別の記事（ pdf ）からのより現代的なレンダリングが興味深いと思われます 。





PPS翻訳では、元の本にある文学への参照を無限に提供していません。 テーブルと写真の番号は元のままです。 元の本はこちらです： algorithmicbotany.org/papers/#abop サイトがダウンしている場合は、pdfで本をダウンロードできます： all 、 第2章のみ。 テキストにスペルや技術的な誤りが含まれている場合は、すぐにPMでお知らせください））