それでは、Adaboost方法論の本質は何ですか？
一番下の行は、参照オブジェクト（平面上の点）のセットがある場合、つまり 値とそれらが属するクラスがあり（たとえば、-1は赤い点、+ 1は青い点）、さらに多くの単純な分類子（プレーンを2つの部分に最小のエラーで分割する垂直線または水平線のセット）があります。最高の分類器を1つ作成できます。 同時に、最終分類子をコンパイルまたはトレーニングするプロセスでは、「悪い」と認識されている標準に重点が置かれます。これはアルゴリズムの適応性であり、学習プロセスでは最も「複雑な」オブジェクトに適応します。
アルゴリズムの擬似コードは、 Wikiで詳しく説明されています。 ここに持ってきます。
擬似コード
与えられた：
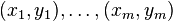どこで 
。
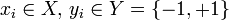初期化
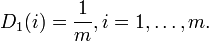
それぞれについて
：
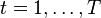*分類子を見つける
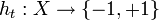これにより、重み付き分類エラーが最小化されます。
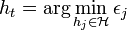どこで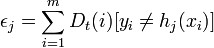 
*値が
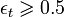その後、停止します。
*選択してください
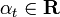通常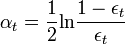 
ここで、tは分類子htの加重誤差です。
*アップデート：
、
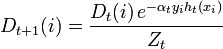ここで、Ztは正規化パラメーターです（Dt + 1が確率分布になるように選択されています。
）
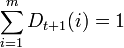結果の分類器を作成します。
。
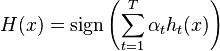さらに、私たちは説明でそれに固執します。
単純な分類器
したがって、単純な分類器です。 先ほど言ったように、これは平面を2つの部分に分割する垂直線または水平線であり、分類エラーを最小限に抑えます。
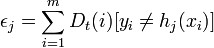（ブール式の角括弧は、真の場合は1、偽の場合は0です）。 C＃では、このようなトレーニングの手順は次のように記述できます。
//単純な分類器のトレーニング
public override void Train(LabeledDataSet< double > trainingSet)
{
// D_i
if (_weights == null )
{
_weights = new double [trainingSet.Count];
for ( int i = 0; i < trainingSet.Count; i++)
_weights[i] = 1.0 / trainingSet.Count;
}
Random rnd = new Random();
double minimumError = double .PositiveInfinity;
_d = -1;
_threshold = double .NaN;
_sign = 0;
//
for ( int d = 0; d < trainingSet.Dimensionality; d++)
{
// ,
if (rnd.NextDouble() < _randomize)
continue ;
// x_d = threshold
double [] data = new double [trainingSet.Count];
int [] indices = new int [trainingSet.Count];
for ( int i = 0; i < trainingSet.Count; i++)
{
data[i] = trainingSet.Data[i][d];
indices[i] = i;
}
Array.Sort(data, indices);
//
double totalError = 0.0;
for ( int i = 0; i < trainingSet.Count; i++)
totalError += _weights[i];
//
double currentError = 0.0;
for ( int i = 0; i < trainingSet.Count; i++)
currentError += trainingSet.Labels[i] == -1 ? _weights[i] : 0.0;
// threshold,
//,
for ( int i = 0; i < trainingSet.Count - 1; i++)
{
//
int index = indices[i];
if (trainingSet.Labels[index] == +1)
currentError += _weights[index];
else
currentError -= _weights[index];
// ,
if (data[i] == data[i + 1])
continue ;
// threshold
double testThreshold = (data[i] + data[i + 1]) / 2.0;
// threshold, ,
if (currentError < minimumError) // _sign = +1
{
minimumError = currentError;
_d = d;
_threshold = testThreshold;
_sign = +1;
}
if ((totalError - currentError) < minimumError) // _sign = -1
{
minimumError = (totalError - currentError);
_d = d;
_threshold = testThreshold;
_sign = -1;
}
}
}
}
気付いた場合、単純な分類器のトレーニング手順は、AdaBoostアルゴリズムの作業中に取得された重みを渡すと、重み付き分類エラーを最小化する分類器が検索されるように記述されます。 次に、C＃のアルゴリズムは次のようになります。
「複雑な」分類器
// AdaBoostで学ぶ
public override void Train(LabeledDataSet< double > trainingSet)
{
// D_i
if (_weights == null )
{
_weights = new double [trainingSet.Count];
for ( int i = 0; i < trainingSet.Count; i++)
_weights[i] = 1.0 / trainingSet.Count;
}
//
for ( int t = _h.Count; t < _numberOfRounds; t++)
{
//
WeakLearner h = _factory();
h.Weights = _weights;
h.Train(trainingSet);
//
int [] hClassification = new int [trainingSet.Count];
double epsilon = 0.0;
for ( int i = 0; i < trainingSet.Count; i++)
{
hClassification[i] = h.Classify(trainingSet.Data[i]);
epsilon += hClassification[i] != trainingSet.Labels[i] ? _weights[i] : 0.0;
}
// epsilon >= 0.5,
if (epsilon >= 0.5)
break ;
// \alpha_{t}
double alpha = 0.5 * Math.Log((1 - epsilon) / epsilon);
// D_i
double weightsSum = 0.0;
for ( int i = 0; i < trainingSet.Count; i++)
{
_weights[i] *= Math.Exp(-alpha * trainingSet.Labels[i] * hClassification[i]);
weightsSum += _weights[i];
}
//
for ( int i = 0; i < trainingSet.Count; i++)
_weights[i] /= weightsSum;
//
_h.Add(h);
_alpha.Add(alpha);
// ,
if (epsilon == 0.0)
break ;
}
}
したがって、最適な分類器h_ {t} \を選択した後、分布D_iに対して、分類器h_ {t} \が正しく識別するオブジェクトx_ {i} \は、正しく識別されないものよりも小さい重みを持ちます。 したがって、アルゴリズムが分布D_ {t + 1}の分類器をテストするとき、前の分類器によって誤って認識されたオブジェクトをより適切に識別する分類器を選択します。
例
そのようなデータの分類の場合：
AdaBoostを使用した分類図は次のようになります。
比較のために、クラスごとに既知の最近傍を決定する簡単なアルゴリズムを各ポイントに与えることができます。 （このようなアルゴリズムのコストが非常に高いことは明らかです。）
おわりに
ご覧のとおり、AdaBoostを使用して構築されたアルゴリズムは、1つの分類器よりもはるかに良好に分類されますが、エラーもあります。 しかし、アルゴリズムのシンプルさとエレガントさにより、彼はデータマイニングのトップ10アルゴリズムに入ることができました。 記事のコードがこのアルゴリズムの理解に役立つことを願っています。
プログラムの完全なソースコードとプログラム自体は、 ここからダウンロードできます 。
PS記事の続きとして、一般的な分類器が弱い分類器の線形関数としてではなく、たとえば2次関数として構築される場合を考えることができます。 この記事の著者は、この場合に2次関数を効果的にトレーニングする方法を見つけたと主張しています。 または、記事の続きで、オブジェクトのクラスが3つ以上ある場合を考えることができます。