1968年 ハンガリーの生物学者であり植物学者であるアリスティド・リンデンマイヤーは、単純な多細胞生物の発達を研究するための数学モデルを提案しました。 このモデルは、Lindenmayerシステム、または単にLシステムと呼ばれます。
主題にあり、物語全体を読みたくない人のために、スクロールダウンして、質問があります。
本文ではL-SystemをLに短縮します。
書き換えます。
Lの主なアイデアは、文字列の要素を常に書き換えることです。 それは何ですか? つまり、書き換えは、いくつかのルールに従って単純な初期オブジェクトの一部を置き換えることにより、複雑なオブジェクトを取得する方法です。 古典的な例はスノーフレークです。 図では、イニシエーターは、フェースがジェネレーターに置き換えられた初期オブジェクトです。 次に、同じことを新しいオブジェクトで行います。 この場合、通常のフラクタル。

Lに戻り、フラクタルとの類推を描くと、Lは最初の単純な公理から始まる特別な規則に従って文字列で動作すると言うことができます。 文法の概念に精通している人は、実際にはLがそうであることにすぐに気付くでしょう。 しかし、L 文法と形式文法の根本的な違いは、規則が行全体、各文字に同時に適用されることです。さらに、終端文字と非終端文字の概念はありません。 つまり、この文法の「結論」は無期限に続く可能性があります。 このモデルがどこから来たのかを考えると、ルールの同時適用が非常に迅速に明らかになります。 生物学では、すべての細胞が時間とともに並行して成長、分裂、発達します。 次の図は、コンテキストフリー(OL)、コンテキスト依存(IL)L、およびチョムスキー階層の他の正式な文法の関係を示しています 。

最も単純なLシステム。
また、チョムスキー分類のように、Lには単純なものから複雑なもの、そして強力なものまで独自の分類があります。
最も単純な例は、決定論的なコンテキストフリーLまたは短縮DOLです。 正式な文法の定義は好きではないので、自分の言葉で言います。 文字の特定のセットがあります-アルファベット。 このアルファベットは、L。が動作する行を記録します-公理-1つ以上の文字の最初の文字列とa→abという形式のルールセット 現在の行からの文字にルールを適用するアルゴリズムの各反復中に、矢印(文字)は矢印の右側にある文字のセットに置き換えられます。 LindenmeyerがモデルLを提案したときに研究した多細胞生物Anabaena catenulaの開発の具体例を検討するのは簡単です。
アルファベットを次の文字で構成します。各文字は特定のセルを示します:a l a r b l b r 。
公理は1文字で構成されます。
ω:a r
そして4つのルール。
p1:a r →a l b r
p2:a l →b l a r
p3:b r →a r
p4:b l →a l
ルールは、成長の過程でどのシンボルがどのシンボルに変わるかを述べています。 写真は、ルールを適用することにより、細胞と発生の「分割」を観察する方法を示しています。
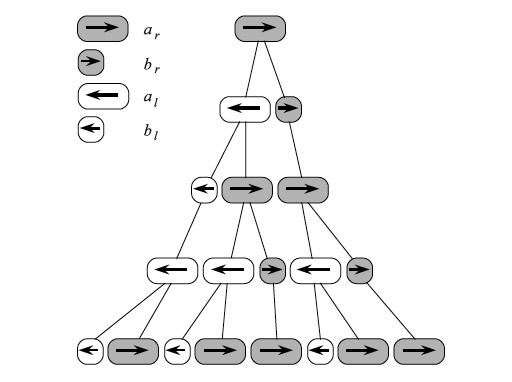
文字列のカメの解釈。
これまで、1次元のバクテリアを描画する方法を見てきましたが、亀を制御し、画面上に図形を描画することを提案する有名な子供向けプログラミング言語LOGOを使用すると、2次元および3次元のフラクタルと繰り返し構造を描画できます。 どうやって? すべてがシンプルです。 各記号が2次元または3次元のカメのコマンドを意味するアルファベットを使用します。
- F-前進して線を引く
- f-何も描かずに前進する
- +-左折
- --右折
- &-断る
- ^-ターンアップ
- \-左に傾く
- /-右に傾く
- | -180度向きを変える
これらのコマンドは、回転角δ、ステップ長、および2次元および3次元空間の基本ベクトルのデフォルト値を使用します。 2次元フラクタルとLを生成するLの例を次の図に示します。

植物および分岐構造。
これより前のすべては、一般に連続曲線です。 もちろん、この方法では、分岐トポロジでプラントをモデル化することは非常に困難です。 このため、アルファベットの文字[および]が追加され、それぞれブランチの開始と終了を示します。 カメがシンボルに出会うと、[現在の状態がスタックに書き込まれ、シンボルが出会うとそこから引き出されます]。
すでにこのような単純な文法を使用すると、木に似た非常に興味深い2次元および3次元のオブジェクトを生成できます。

より複雑な文法。
もちろん、科学は静止していませんでした。今では、前述の単純なDOLから始まるLの強固な階層構造があります。
確率的L
確率的Lsは、ルールの実行の確率を指定する機能を追加します。一般的な場合、異なるルールは左側に同じシンボルを持つことができるため、決定論的ではありません。 これにより、結果の構造にランダム性の要素が導入されます。
状況依存L
正式な文法の文脈依存性と同様に、Lでは規則の構文は複雑であり、置換された文字の環境を考慮します。
パラメトリックL
可変パラメーター(おそらく複数)が各シンボルに追加されます。これにより、たとえば、+と-の回転角度の指定、ステップ長と線の太さ、ルールの適用条件の確認、反復回数のカウント、「信号」の送受信が可能になります。 パラメトリックLの例
ω : B(2)A(4, 4)
p1 : A(x, y) :y <= 3 → A(x ∗ 2, x + y)
p2 : A(x, y) :y > 3 → B(x)A(x/y, 0)
p3 : B(x) :x < 1 → C
p4 : B(x) :x >= 1 → B(x − 1)
パラメトリックコンテキストセンシティブLを使用すると、生化学プロセスと環境を考慮して、多細胞生物と植物の成長をシミュレートできます。 たとえば、以前の友人であるアナベナカテヌラはより複雑な形式です。 本からの例[1]。
本に書かれているように、この細菌は栄養細胞と異質細胞の2種類の細胞で構成されています。 通常、栄養細胞は2つの類似した栄養細胞に分割されます。 ただし、場合によっては、栄養細胞は異質細胞になります。 それらの分布はよく観察されたパターンに従い、隣接するヘテロシストはほぼ同じ数の栄養細胞によって分離されます。 しかし、成長中に体はどのように異嚢胞間の一定の距離を維持するのでしょうか? 提案されたモデルは、生物学の観点からこの現象を説明しています。 ヘテロシストの配置は、これらの細胞が産生する窒素化合物によって調節され、窒素化合物は体の他の細胞に伝達され、栄養細胞で消費されると考えられています。 若い栄養細胞のこれらの化合物の含有量が特定のレベルを下回ると、この細胞は異質細胞になります。
以下のLシステムは、前述の観点から細菌の増殖をモデル化しています。
#defineは、Lで使用される定数に値を割り当てます。
#includeはヘテロシストフォーム、この場合は円をロードします。
細胞はF(s、t、c)モジュールで表されます。sは細胞の長さ、tは細胞タイプ(0はヘテロシスト、1と2は栄養細胞)、cは窒素濃度です。
#define CH 900 /* high concentration */
#define CT 0.4 /* concentration threshold */
#define ST 3.9 /* segment size threshold */
#include H /* heterocyst shape specification */
#ignore f ∼ H
ω : -(90)F(0,0,CH)F(4,1,CH)F(0,0,CH)
p1 : F(s,t,c) : t=1 & s>=6 → F(s/3*2,2,c)f(1)F(s/3,1,c)
p2 : F(s,t,c) : t=2 & s>=6 → F(s/3,2,c)f(1)F(s/3*2,1,c)
p3 : F(h,i,k) < F(s,t,c) > F(o,p,r) : s>ST|c>CT → F(s+.1,t,c+0.25*(k+r-3*c))
p4 : F(h,i,k) < F(s,t,c) > F(o,p,r) : !(s>ST|c>CT) → F(0,0,CH) ∼ H(1)
p5 : H(s) : s<3 → H(s*1.1)

皮下注射。
ここで、たとえば、インターネットを征服した最近の皮下注射は、本質的に最も単純なLの組み合わせです。
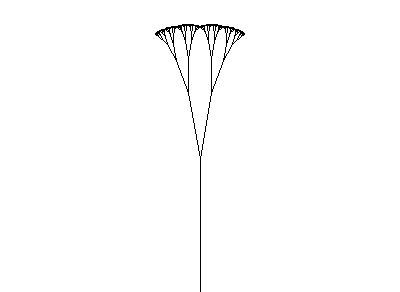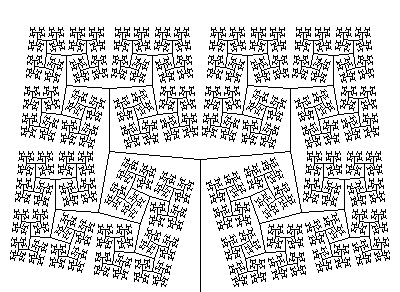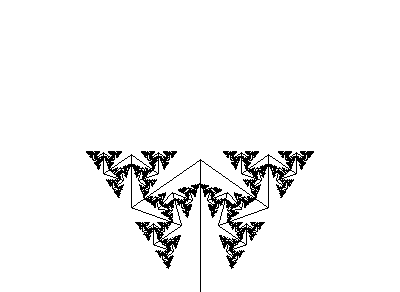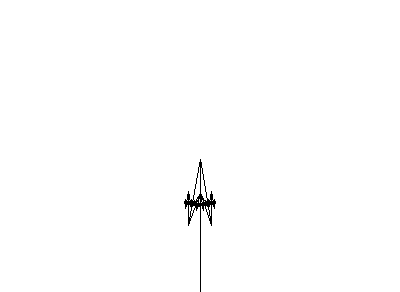
#define R 1.456
ω : A(1)
p1 : A(s) → F(s)[+A(s/R)][−A(s/R)]
より高度な。
これは理論の表面的な説明であり、実際の応用の小さな例です。 次に好奇心research盛な研究者を待っていますか?
- 二次元および三次元の多細胞生物の成長のモデリング
- 木の成長アニメーション
- 環境モデリング
- 化学的および生物学的プロセスと成長関数のシミュレーション
- 表面生成のためのLアプリケーション
- 不動産や都市のモデリングなど、その他のさまざまなユースケース
例。




使用します。
80年代後半に、Lは植物モデルを視覚化するために使用されました。 現在、コンピューターの機能ははるかに進んでいます。 多くのゲームおよび3Dモデリングツールは、L-Systemsを含む手続き型コンテンツ生成を使用します。 ご覧のとおり、一連の単純なルールから、膨大な数の異なる植物を取得し、それらを使用してフィールド全体を植えることができます。
エディターのうち、私自身はHoudiniでLを使用していますが、他のパッケージ用のプラグインもあると聞きました。 いわゆるバーチャルラボでは、Lを実験してアニメーション化できます。
文法法は、いわゆるシェイプグラマーでも使用されますが、これについては後で詳しく説明します。
インターネット上のいくつかの投稿。
http://avalter.blogspot.com/2009/08/2d-l.html
書籍および追加資料。
一般的に言えば、利用可能な唯一の本は、 The Algorithmic Beauty of Plantsです。 また、古いランダムな記事はインターネット上に散らばっています。 多かれ少なかれ新しいものは、 大量のお金でspringerlink.comで、または無料で研究所の図書館で見つけることができます。
私が言えることは、素材が十分ではないということです。
生物学に近い考え。
私自身は生物学とはまったく関係がありませんが、私は数学のマスターであり、いくつかの無邪気な趣味を持っています。 しかし、私はL-Systemsのアイデアが本当に好きです。 優れた機能を備えたシンプルさ。 むかしむかし、私はDNAに私に関する完全な情報がどのように含まれているかを考えました。 すべてのセルに関するすべての情報を各セルに詰め込むにはどうすればよいですか? しかし、とにかく、L理論は私の目を開いたと言えます! 私のDNAには、私がどのように見えるかではなく、私を組み立てる方法が書かれています(一般的に)。 Lのルールセットに似たもので、タンパク質合成にのみ関連しています。
シンプルなモデルは、あなたとの私たちの生活をはっきりと説明しています。
さらに-ルールを「DNA」に変換し、遺伝的アルゴリズムを使用して仮想マルチセルルールを成長させます。
科学的思考。
材料や記事を共有するために、Lの科学的要素にも興味のある人を見つけたいです。 たまたま、私は現在、アップグレードされたL-Systemsのコンセプトに取り組んでいますが、過去5年間にこのトピックについて書かれた内容をレビューすることはできません。 私は車輪を再発明したくありません。
書籍の著者に連絡することはできませんでした;留守番電話は、彼が1月(8
また、3Dモデリングのシェイプグラマーに関する情報も探しています。 パラメーターから宇宙船を生成するタスクがあります、ご存知のように、小さなパーツの束を持つこのような巨大なギズモは、SGの理想的な候補です。 PythonでHoudiniのプラグインを本当に作成する必要がありますか?