イントロ
この記事から、既知のデータ構造ではなく、実際のアプリケーションに関する一連の記事を開始します。
私の記事では、JavaとHaskellの2つの言語のコード例を同時に示します。 これにより、プログラミングの命令型と機能型を比較し、両方の長所と短所を確認することが可能になります。
バイナリ検索ツリーから始めることにしました。これはかなり基本的なものであると同時に、興味深いものであり、実用的なアプリケーションだけでなく、多数の変更やバリエーションもあります。
なぜこれが必要ですか?
通常、バイナリ検索ツリーは、セットと連想配列を実装するために使用されます(たとえば、C ++でのセットとマッピング、またはJavaでのTreeSetとTreeMap)。 より複雑なアプリケーションには、ロープ(以下の記事のいずれかで説明します)、主に「走査線」に基づくアルゴリズムの計算幾何学のさまざまなアルゴリズムが含まれます。
この記事では、連想配列の例を使用してツリーを調べます。 連想配列は、インデックス(通常はキーと呼ばれます)が任意である一般化された配列です。
さあ、始めましょう
バイナリツリーは、頂点とそれらの間の接続で構成されます。 より具体的には、ツリーには明確なルート頂点があり、各頂点には左と右の息子を含めることができます。 言葉では少し複雑に聞こえますが、写真を見るとすべてが明確になります。
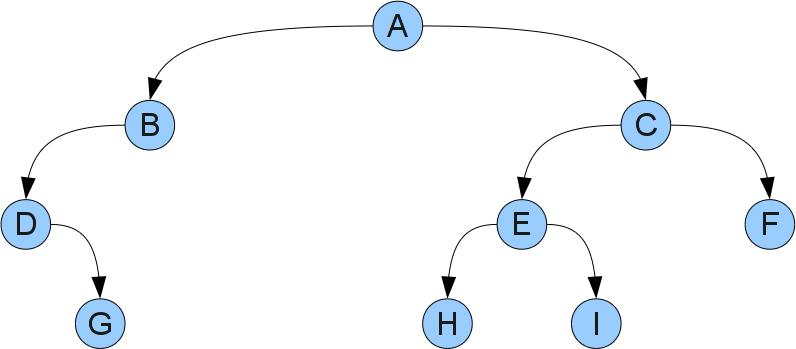
このツリーのルートは頂点Aになります。頂点Dには左息子がなく、頂点Bには右息子があり、頂点G、H、F、およびIには両方があることがわかります。 息子のいない山は通常葉と呼ばれます。
各頂点Xは、頂点、その息子、息子の息子などで構成される独自のツリーに関連付けることができます。 Xの左と右のサブツリーは、それぞれXの左と右の息子にルートを持つサブツリーと呼ばれます。
ツリー内のデータは、頂点に保存されます。 プログラムでは、ツリートップは通常、データと左と右の息子への2つの参照を格納する構造によって表されます。 欠落している頂点は、nullまたは特別なLeafコンストラクターによって示されます。
data Ord key => BSTree key value = Leaf | Branch key value (BSTree key value) (BSTree key value) deriving (Show)
static class Node<T1, T2> { T1 key; T2 value; Node<T1, T2> left, right; Node(T1 key, T2 value) { this.key = key; this.value = value; } }
例からわかるように、互いに比較できるようにキーが必要です(haskellの
Ord a
と
T1 implements Comparable<T1>
はjavaの
T1 implements Comparable<T1>
ます)。 これはすべて簡単なことではありません。ツリーを有効にするには、いくつかのルールに従ってデータを格納する必要があります。
これらのルールは何ですか? 簡単です。キーxが頂点Xに格納されている場合、xよりも小さい(それぞれ大きい)キーのみを左(右)サブツリーに格納する必要があります。 私たちは説明します:
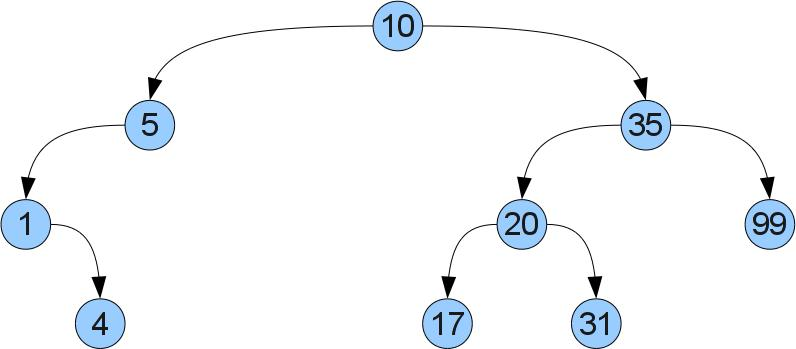
そのような注文は私たちに何を与えますか? ツリーで必要なキーxを簡単に見つけることができること! xをルート値と比較するだけです。 それらが等しい場合、必要なものが見つかりました。 xが小さい(大きい)場合、左(それぞれ右)のサブツリーにのみ表示できます。 たとえば、17番のツリーを検索するとします。
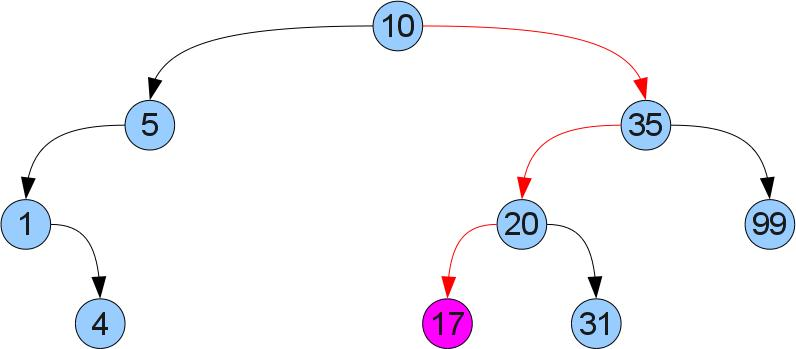
キー値を受け取る関数:
get :: Ord key => BSTree key value -> key -> Maybe value get Leaf _ = Nothing get (Branch key value left right) k | k < key = get left k | k > key = get right k | k == key = Just value
public T2 get(T1 k) { Node<T1, T2> x = root; while (x != null) { int cmp = k.compareTo(x.key); if (cmp == 0) { return x.value; } if (cmp < 0) { x = x.left; } else { x = x.right; } } return null; }
ツリーに追加
ここで、新しいキー/値のペア(a、b)を追加する操作を試してみましょう。 これを行うには、同じキーを持つ頂点が見つかるまで、または行方不明の息子に到達するまで、get関数のようにツリーを下っていきます。 同じキーを持つ頂点が見つかったら、対応する値を変更するだけです。 そうでない場合、順序を乱さないために、この場所に新しい頂点を挿入する必要があることを正確に理解するのは簡単です。 前の図のツリーにキー42を挿入することを検討してください。
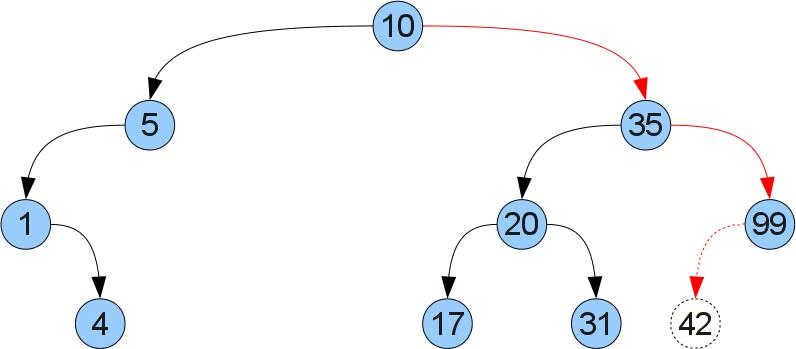
コード:
add :: Ord key => BSTree key value -> key -> value -> BSTree key value add Leaf kv = Branch kv Leaf Leaf add (Branch key value left right) kv | k < key = Branch key value (add left kv) right | k > key = Branch key value left (add right kv) | k == key = Branch key value left right
public void add(T1 k, T2 v) { Node<T1, T2> x = root, y = null; while (x != null) { int cmp = k.compareTo(x.key); if (cmp == 0) { x.value = v; return; } else { y = x; if (cmp < 0) { x = x.left; } else { x = x.right; } } } Node<T1, T2> newNode = new Node<T1, T2>(k, v); if (y == null) { root = newNode; } else { if (k.compareTo(y.key) < 0) { y.left = newNode; } else { y.right = newNode; } } }
機能的アプローチの長所と短所についての叙情的な余談
両方の言語の例を注意深く検討すると、機能実装と命令型実装の動作に多少の違いが見られます:Javaで利用可能な頂点のデータとリンクを変更するだけの場合、haskellバージョンは再帰によって横断されるパス全体に沿って新しい頂点を作成します。 これは、純粋に機能的な言語では破壊的な割り当てができないためです。 明らかに、これによりパフォーマンスが低下し、メモリ消費が増加します。 一方、このアプローチにはプラスの側面があります。副作用がないため、プログラムの機能を理解しやすくなります。 これについては、関数型プログラミングに関するほぼすべての教科書または入門記事で詳しく読むことができます。
同じ記事で、機能的アプローチの別の結果に注意を喚起したいと思います。新しい要素をツリーに追加した後でも、古いバージョンは引き続き利用可能です! この効果により、命令型言語の実装を含むロープが機能し、従来のアプローチよりも漸近的に高速な操作で文字列を実装できます。 ロープについては、次のいずれかの記事で説明します。
ラムに戻る
次に、この記事で最も難しい操作、つまりキーxをツリーから削除します。 そもそも、前と同じように、ツリーの最上部を見つけます。 現在、2つのケースが発生しています。 ケース1(番号5を削除):

取り外したトップには右の息子がいないことがわかります。 次に、順序を壊さずに、それを削除し、代わりに左のサブツリーを挿入できます。
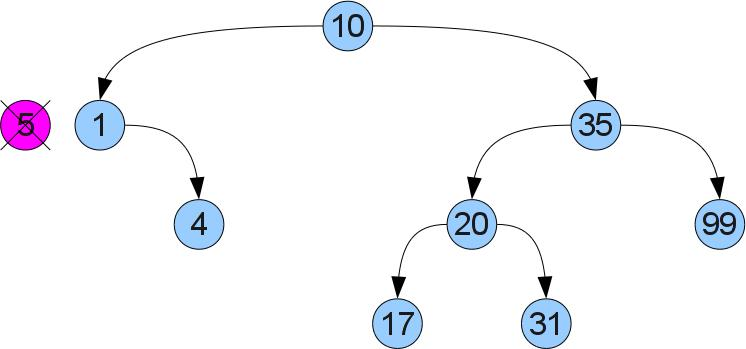
右の息子がいる場合、ケース2は明らかです(頂点5を再度削除しますが、少し異なるツリーから削除します)。
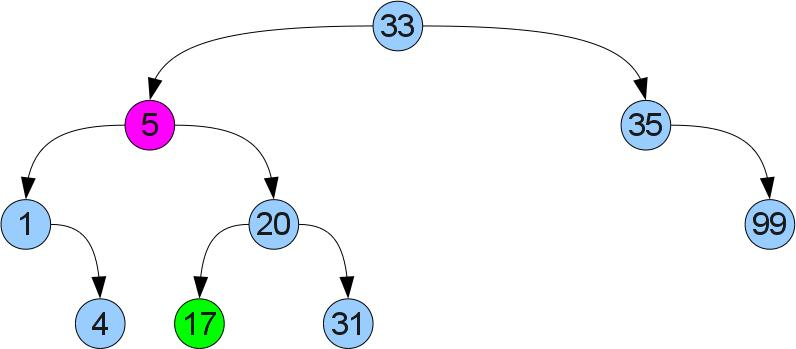
それは成功しません-左の息子はすでに右の息子を持っているかもしれません。 異なる行動をとります:正しいサブツリーで最小値を見つけます。 あなたが右の息子から始めて左にずっと行くとそれが見つかることは明らかです。 見つかった最小値には左の息子がないため、ケース1と同様に切り取り、削除された頂点の代わりに貼り付けることができます。 正しいサブツリーでは最小であるという事実により、順序付けプロパティは違反されません。
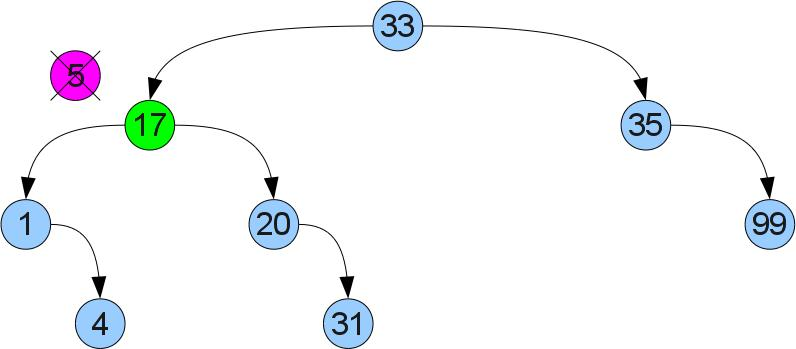
削除の実装:
remove :: Ord key => BSTree key value -> key -> BSTree key value remove Leaf _ = Leaf remove (Branch key value left right) k | k < key = Branch key value (remove left k) right | k > key = Branch key value left (remove right k) | k == key = if isLeaf right then left else Branch leftmostA leftmostB left right' where isLeaf Leaf = True isLeaf _ = False ((leftmostA, leftmostB), right') = deleteLeftmost right deleteLeftmost (Branch key value Leaf right) = ((key, value), right) deleteLeftmost (Branch key value left right) = (pair, Branch key value left' right) where (pair, left') = deleteLeftmost left
public void remove(T1 k) { Node<T1, T2> x = root, y = null; while (x != null) { int cmp = k.compareTo(x.key); if (cmp == 0) { break; } else { y = x; if (cmp < 0) { x = x.left; } else { x = x.right; } } } if (x == null) { return; } if (x.right == null) { if (y == null) { root = x.left; } else { if (x == y.left) { y.left = x.left; } else { y.right = x.left; } } } else { Node<T1, T2> leftMost = x.right; y = null; while (leftMost.left != null) { y = leftMost; leftMost = leftMost.left; } if (y != null) { y.left = leftMost.right; } else { x.right = leftMost.right; } x.key = leftMost.key; x.value = leftMost.value; } }
デザートの場合、テストに使用したいくつかの機能:
fromList :: Ord key => [(key, value)] -> BSTree key value fromList = foldr (\(key, value) tree -> add tree key value) Leaf toList :: Ord key => BSTree key value -> [(key, value)] toList tree = toList' tree [] where toList' Leaf list = list toList' (Branch key value left right) list = toList' left ((key, value):(toList' left list))
これはどのように便利ですか?
読者は、ペアのリスト[(key、value)]だけを保持できる場合に、なぜこのような困難が必要なのかと尋ねるかもしれません。 答えは簡単です-ツリー操作は高速です。 リストによって実装される場合、すべての関数はO(n)アクションを必要とします。nは構造のサイズです。 (表記O(f(n))は、おおよそ「f(n)に比例する」ことを意味します。より正確な説明と詳細については、 こちらを参照してください)。 ツリーの操作はO(h)に対して機能します。hはツリーの最大の深さ(深さはルートからトップまでの距離)です。 最適なケースでは、すべての葉の深さが同じ場合、ツリーにはn = 2 ^ hの頂点があります。 したがって、ツリーの操作の最適度に近い複雑さはO(log(n))になります。 残念ながら、最悪の場合、ツリーは縮退する可能性があり、操作の複雑さは、たとえばそのようなツリーのリストのようになります(番号1..nを順番に挿入すると判明します)。
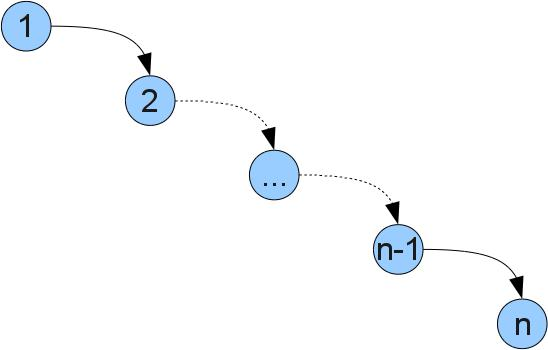
幸いなことに、ツリーを実装して、一連の操作中にツリーの最適な深さが維持されるようにする方法があります。 このようなツリーは、バランスと呼ばれます。 これらには、赤黒木、AVL木、スプレー木などが含まれます。
次のシリーズの発表
次の記事では、バランスのとれたさまざまなツリーとその長所と短所について簡単に説明します。 次の記事では、いくつか(おそらく複数)について、実装について詳しく説明します。 その後、ロープの実装と、バランスの取れたツリーの他の可能な拡張およびアプリケーションについて説明します。
連絡を取り合いましょう!
便利なリンク
サンプルソースコード:
ハスケルで
Javaで
ウィキペディアの記事
BSTインタラクティブビジュアライザー
また、Kormen T.、Leiserson Ch。、Rivest R .:「Algorithms:construction and analysis」という本を読むことを強くお勧めします。これは、アルゴリズムとデータ構造に関する優れた教科書です。