コメントを読んだ後、チェスやチェッカーなどをプレイするための最も一般的なアルゴリズムの動作原理は誰もが知っているわけではないという結論に達しました。
同時に、このゲームに固有の特定の数量と評価を計算する方法がある場合、何かを再生するプログラムを作成するタスクは簡単です。
チェスに関連したアルファ-ベータのカットオフとミニマックス法について説明します(文献では、より一般的な用語である「フェースアンドバウンドメソッド」と「ブランチアンドバウンドメソッド」も見つけることができます)
ゲーム中はいつでも、各プレーヤーに対して、ルールで許可されているいくつかの動きがあります。 有限だとしましょう。 それに応じて、2番目のプレーヤーは、有限の数の動きを行うこともできます。 ゲームをループさせる可能性を除外すると、ポジションとそれらの間の遷移の総数は多くなりますが、もちろんです。 チェスのルールはまさにそれです。
それはもっと簡単に思えます。完全な検索を完了し、ゲームに関するすべてを知っています。 コンピューターを失うことはできません。
ただし、ポジションの数が非常に多いため、ゲームの完全な分析は事実上不可能です(クラシックな3x3三目並べと同様に豊富なゲーム戦略を除く)。
したがって、実際には、次のことが行われます。
1.分析的、専門的、または前例の推論方法により、取締役会のポジションを評価する機能が構築されます。 通常、この評価は軸上でランク付けされます。つまり、白の場合は収益性が高く、黒の場合は収益が低くなり、白の収益性は低下します(いわゆるゼロサムゲーム)。
2.動きの不完全なツリーが構築されています。 同時に、計算される半分の動きの数は、利用可能なコンピューティングリソースによって実際に決定されます(添付プログラムは7つの半分の動きを計算しますが、これは現代のプログラムではかなり控えめです)
3.可能な動きの木の適度にインテリジェントな分析が実行され、その間に意図的に最適でない分岐が切り捨てられ、より有望な分岐が深く計算されます。 これは、有名なアルファベータ手順が実行される場所です。
そして今、同じことですが、より形式的かつ厳密に (プレゼンテーションは主にD. KnutとR. MooreによるPavel Dubnerの翻訳の記事に基づいています ):
指定 :
p-位置
f(p)は、ゲーム終了時の「私たち」のプレイヤーのゲインを推定する数値関数です(これらの位置pは端末とも呼ばれます)
F(p)は、非終端位置での「私たちの」プレーヤーのゲインを推定する数値関数です
2番目のプレーヤーも自分のために最善の方法で行動するという事実から進みます。
次に:
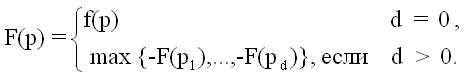
微妙な考慮事項がありますが、クヌートとムーアはそれを完全に定式化したので、引用します。
ただし、悪いプレーヤーや別の最適性の原則に従って行動するプレーヤーに対して必ずしも良いとは限らない非常に慎重な戦略の結果を反映していることに注意してください。 たとえば、位置p1とp2に2つの動きがあり、p1が引き分け(勝利0)を保証し、勝つ機会を与えない一方で、対戦相手が非常に細い勝利の動きを見るとp2が勝つ機会を与えるとします。 このような状況では、対戦相手が全能で全能であることを確信できない限り、p2でリスクのある動きを好むかもしれません。 このようにして人々がチェスプログラムに勝つことは非常に可能です。
全深検索 :
int F( void *p)
{
int res,i,t,d,m;
// ps ( d)
possibles(p, ps, &d);
if (!d) res=f(p) else
{
m = -infinity;
for (i=1;i<=d;i++)
{
t = -F(ps[i]);
if (t > m) m=t;
}
res = m;
}
return res
* This source code was highlighted with Source Code Highlighter .
この検索は再帰的であり、非常に長い間機能しますが、最適な戦略を見つけることが保証されています。
既に見つかったソリューションより明らかに悪い移動ツリーのブランチを考慮することなく、アルゴリズムを最適化できます(これは、ブランチアンドバウンドメソッドと呼ばれます)。
分枝限定法の考え方は、次のアルゴリズムによって実装されます 。
int F1( void *p, int bound)
{
int res,i,t,d,m;
// ps ( d)
possibles(p, ps, &d);
if (!d) res=f(p) else
{
m = -infinity;
for (i=1;(i<=d) && (m<bound);i++)
{
t = -F1(ps[i],-m);
if (t > m) m=t;
}
res = m;
}
return res;
}
* This source code was highlighted with Source Code Highlighter .
この変更により、最適なソリューションも見つかります。
すべての末端頂点に推定がある意図的に有限なゲームツリーの分析の場合、検索の上限と下限を入力することができますが、検索スペースを削減し、リソースを節約できます。
アルファベータクリッピングは、次のコードで実装されます 。
int F1( void *p, int alpha, int beta)
{
int res,i,t,d,m;
// ps ( d)
possibles(p, ps, &d);
if (!d) res=f(p) else
{
m = alpha;
for (i=1;(i<=d) && (m<beta);i++)
{
t = -F2(ps[i],-beta,-m);
if (t > m) m=t;
}
res = m;
}
return res;
}
* This source code was highlighted with Source Code Highlighter .
そのような最適化は悪名高い解決策を見つけます 。
実際には、チェスは言うまでもなく、最も単純なゲームであっても、端末の位置の完全な列挙を整理することはできません。 したがって、位置のおおよその評価という重要なタスクが発生します。 正しいマットが位置に多くの利点を与えることは明らかですが、数字の位置、王の安全、数値の優位性、キャスティングの可能性など、すべてが考慮されます。 実装の詳細に応じて、ロボットは慎重すぎるか、逆に無謀に取引所に身を投げる場合があります。
評価関数を使用すると、アルゴリズムの数学的な厳密さが失われます。 評価関数と同じくらい良いでしょう。
関数F2の最初の呼び出しには、アルファとベータとして異なる符号の無限大が含まれることは明らかです。
動きのツリーの例:

最後の図の追加説明はこちら: ソース
別の問題は、パーティーの始まりです。 それは終わりまで遠い、見通しは霧であり、誰も子供にマットを与えない。 したがって、原則として、調査された開口部のライブラリが使用されます。 対戦相手がチェスの戦術の観点から理解できない何かをした場合、上記のアナライザーがオンになります。
原則として、上記のすべては比較的単純です。 私の生徒たちは、2年目の勉強の後、3人が3週間でこれらのチェスの駒を積み上げました。 そこではすべてが質的に行われ、成長する余地があります。