👃🏾 👨‍👩‍👦‍👦 🧛🏾 リキッドリサイズ 💚 🛌 👨🏿‍🔧

画像コンテンツを考慮したLiquid Resizeスケーリングテクノロジーについては、おそらく既に聞いたことがあるでしょう。すべてがどのように機能し、自分ですべてを実装する方法に興味がある場合は、読んでください（慎重に、たくさんの写真）。

（UFOが飛び込んで、この図面をここに伸ばしました）

私は友人の要請で記事を投稿しました。友人はアカウントを持っていないため、Habrに載せることができません。 あなたの利点のおかげで、著者は招待状を持っています、そして今、彼は私たちと一緒にいます：コッター 。

内容

シームカービングとは
この記事を読む際の注意事項
一般的なアルゴリズムスキーム
ポイントエネルギー計算
総エネルギーが最小のチェーンを見つける
図面の削減
図面の拡大
例
まとめ

シームカービングとは

Seam Carvingは、画像コンテンツを考慮に入れた画像サイズ変更アルゴリズムです（作成者がそれを呼ぶように-Content-Aware Image Resizing Algorithm）。 2007年に初めて実証され、大きな関心を呼びました。おそらくこのトピックに関する記事が既にあったので、Habrの多くの読者は彼について聞いたでしょう。

その後、疑問が生じます。このアルゴリズムは画像の内容をどのように考慮しますか？理論的には、ここではすべてが単純です-最初に、画像のさまざまな部分の重要性が計算され、その後、アルゴリズムに従ってサイズがそれほど重要ではない部分のみが計算されます。実際には、このアルゴリズムを実装するには、画像の重要な部分をどのように判断するか、画像の重要でない部分を見つけて圧縮する方法など、いくつかの質問を解決する必要があります。

この記事では、これらに加えて、この問題を解決するときに生じる他の多くの質問に答えようとしました。

すでに私が終わったものを見たいと思っている人は、記事の最後で画像の例とコメント付きソースのデモプログラムを見つけることができます。

この記事を読む際の注意事項

記事自体の前に、いくつかの規則を規定したいと思います。

まず第一に。この記事では、「エネルギー」という用語をよく使用しますが、この用語の正確性についてはわかりません。そして、著者自身が英語の単語「エネルギー」と呼んでいるので、私はそれを使います。ポイントのエネルギーは、画像におけるその重要性を意味します。より多くのエネルギー、より重要なポイント。

第二に。この記事では、水平方向のサイズ変更のみを扱います。両方の方向に同時にサイズ変更する場合、原理は同じままで、ピクセルの垂直チェーンだけでなく、水平チェーンも考慮しているだけです。

第三に。 C＃/。NETで書いた経験はありません。プログラムを作成するためのプラットフォーム/言語の選択は、理解するコードのシンプルさと聴衆の幅広いリーチによるものでした。したがって、プログラム内で無効または「プレドネ」ではない何かを書いた場合、それに注意を払わないでください。これはプログラムの本質ではありません。

4番目。ロシア語は私の母国語ではないので、間違いの可能性があることを残念に思います。

そして最後の1つ。プログラムコードが最適ではありません。コードの単純さとコードの最適性の間で、単純さを選択しました。したがって、このアルゴリズムをどこかで使用する場合は、タスクに合わせて最適化します。幸いなことに、そこには最適化の余地があります。

ここで、実際に、私たちは前奏曲を終えました。今、最も興味深いものに目を向けます...

一般的なアルゴリズムスキーム

アルゴリズム全体は、次のコンポーネントで構成されています。

各ポイントのエネルギーを見つける。この段階で、これらのデータに基づいて、画像のどの部分がより重要で、どの部分がそれほど重要でないかを見つける必要があります。その後、画像サイズを変更します。
このチェーンに入るピクセルの総エネルギーが最小になるように、ピクセルの垂直チェーンを見つける。ピクセルチェーンは、各行で正確に1つのピクセルが選択され、その中の隣接するピクセルが辺または角で接続されているピクセルのセットです。このようなチェーンが見つかった場合、画像のコンテンツへの影響を最小限に抑えながら、画像から削除できます。
最小限のエネルギーでチェーンを見つけた場合、画像を縮小する必要がある場合にのみチェーンを削除でき、画像を拡大する必要がある場合にはストレッチできます。

次に、各項目をさらに詳しく検討します。

ポイントエネルギー計算

まず、画像のどの部分が重要で、どの部分が重要でないかを判断する必要があります。

この問題を解決するために、アルゴリズムの作成者は、各ピクセルについて「エネルギー」、つまり、この画像でこのピクセルが重要であるかどうかを示す条件インジケーター（オウム）を計算することを提案します。

原則として、これを行うには多くの方法があります。最も単純な方法（たとえば、隣接するものと比較して色の変化を数える）からかなり複雑な方法（たとえば、人の注意を分析する）までです。著者自身によると、彼らは多くのエネルギー関数をテストし、最も単純な関数の1つが最良の結果の1つを与えました。したがって、この機能を使用します。ここにあります：

この式を見て、分析を思い出す必要のある派生物を見るのが怖いのなら、無駄です。実際、これは非常に単純に定式化されています。ピクセルのエネルギーは、指定されたピクセルと比較して、隣接するピクセルの色の変化に等しくなります。つまり、特定のピクセルと隣接するピクセルの色の差が大きいほど、そのエネルギーは大きくなります。

次に、実際のエネルギー計算の実装を検討します。イメージポイントをその強度で特徴付けます。次の3x3ドット画像があります。

まず、ピクセルとその隣接ピクセル（右と下）の強度の差を法として計算し、次にこれらの値の算術平均としてこのピクセルのエネルギーを計算します。

選択したピクセルの場合：右側の隣のピクセルと8の差は、下部の隣のピクセルと3の差です。算術平均は（8 + 3）/ 2 = 5.5です。しかし、整数を扱う方がより便利で高速であり、そのような精度は不要であるため、小数部分は破棄します。つまり、選択したピクセルのエネルギーは5です。

同様に、残りのピクセルについて計算します。この場合、右端と下端に極端なピクセルがあるのは、右または下に隣接するピクセルのみであるため、それらの場合、差の値は算術平均になります。右下隅のピクセルには、そのような近傍はまったくないため、そのエネルギーを0として取得します。理論的にはエネルギーを計算することもできますが、実際には無視できるため、生活を複雑にすることはありません。

その結果、次のピクセルエネルギーのマトリックスを取得します。

ピクセルが強度だけでなく、R、G、Bの強度値によって別々に特徴付けられている場合、ピクセルエネルギーは各成分のエネルギーの合計に等しくなります。

画像のエネルギーマップの例：

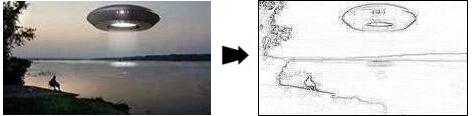
この図では、エネルギーマップの色が濃いほど、エネルギーが多くなります。

次の関数を使用してピクセルエネルギーの検出を実装しました。

private void FindEnergy() { for (int i = 0; i < imgHeight; i++) for (int j = 0; j < imgWidth; j++) { energy[i, j] = 0; //     R, G, B for (int k = 0; k < 3; k++) { int sum = 0, count = 0; //     ,    sum        if (i != imgHeight - 1) { count++; sum += Math.Abs((int)image[i, j, k] - (int)image[i + 1, j, k]); } //     ,    sum        if (j != imgWidth - 1) { count++; sum += Math.Abs((int)image[i, j, k] - (int)image[i, j + 1, k]); } //   energy         k-  (   R, G  B) if (count != 0) energy[i, j] += sum / count; } } }

この関数はグローバル変数で機能します：energy-エネルギーが書き込まれる配列とimage-画像が保存される配列。

総エネルギーが最小のチェーンを見つける

各ピクセルのエネルギー値はすでにありますが、最小エネルギー値を持つピクセルを選択する必要があります。しかし、任意のピクセルをピックアップ/追加し始めると、画像自体が単純に外に出て認識できないほど変形します。もちろん、この結果は私たちには合いません。したがって、最初にピクセルのチェーンを選択してから、それらを削除または追加する必要があります。そして、任意のチェーンではなく、「正しいチェーン」。

「正しい」チェーンとは、画像の各行で正確に1ピクセルが選択され、隣接する行のピクセルが辺または角で「接続」されるようなポイントのセットです。

「正しい」チェーンの例：

「間違った」チェーンの例：

これで、「正しい」チェーンを削除する必要があることがわかったので、イメージをあまり損なうことはありません。しかし、次に選択するチェーンはどれですか？アルゴリズムの作成者は、除去/ストレッチのためにそれらのチェーンを選択することを提案します。それに含まれるピクセルエネルギーの合計は最小です。

これは非常に自然な疑問を招きます：そのようなチェーンをどのように見つけるのですか？

オプション1-すべてのチェーンをソートし、それらを要約して、最小量で見つけます。もちろん、このオプションは興味深いものですが、小さな画像でも処理するためには永遠に待たなければなりません:)在庫が永遠にある場合、徹底的な検索、開始、待機のコードを記述します。短時間で結果を確認したい場合は、先に進んでください。

ここで、動的プログラミングの助けになります。詳細には触れず、プログラミングの「ダイナミズム」が何であるかを正確に示しません（ところで、「プログラミング」という用語はここでコードを書くこととは関係ありません）、すぐにアルゴリズムに直接進みます。誰かが「動的プログラミング」が何であるかを知らず、知りたい場合は、ウィキペディアまたは他のソースでそれについて読むことができます。

まず、ピクセルエネルギーを持つ配列と同じサイズの新しい配列を作成します。この配列では、ピクセルごとに、ピクセルの最小チェーンの要素の合計を書き込みます。これは、画像の上端から始まり、このピクセルで終わります。

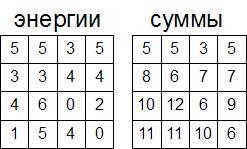
例によって計算プロセスを示します。各ピクセルのエネルギー値を持つ配列があるとします：

この配列の要素を行ごとに計算します-最初から最後まで。一番上の行では、この配列の要素は配列の要素と等しくなります。そのような各要素から構築できるチェーンは1つだけであるためです（すべてユニット長）。

次に、2行目を計算しましょう。選択したセルを検討してください。このセルからチェーンを構築するには、図に示すように3つの方法があります。これら3つの方法のうち、最小値を選択する必要があります（最小チェーンの正確な合計を考慮するため）。選択したセルの場合、これは合計3のチェーンになり、このチェーンにセル自体のエネルギーを追加します。したがって、このセルには数字7（3と4の合計）を書き込みます。同様に、2行目のすべての要素のすべての合計を計算します。

3行目に進みましょう。原則として、3行目は2行目に類似していると見なされます。選択したセルをもう一度見てみましょう。それから、そのようなチェーンを形成できます：

このセルと長さ8の最小チェーン。
このセルと長さ6の最小チェーン。
このセルと長さ7の最小チェーン。

これらのオプションのうち、再び最小値（6）を選択し、セル自体のエネルギーを追加します（6）。このセルの値は12です。同様に、3行目の残りの要素を検討します。

この方法ですべての行を計算した後、結果として次の配列を取得します。

この配列の計算を形式化すると、次の式が得られます。

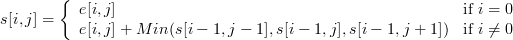
ここで、sは合計の配列、eはエネルギーの配列です。

合計の配列を計算する私の実装：

 private void FindSum() { //     sum  energy   for (int j = 0; j < imgWidth; j++) sum[0, j] = energy[0, j]; //       (i,j)  sum   // energy[i,j] + MIN ( sum[i-1, j-1], sum[i-1, j], sum[i-1, j+1]) for (int i = 1; i < imgHeight; i++) for (int j = 0; j < imgWidth; j++) { sum[i, j] = sum[i - 1, j]; if (j > 0 && sum[i - 1, j - 1] < sum[i, j]) sum[i, j] = sum[i - 1, j - 1]; if (j < imgWidth - 1 && sum[i - 1, j + 1] < sum[i, j]) sum[i, j] = sum[i - 1, j + 1]; sum[i, j] += energy[i, j]; } }

この関数は、グローバル変数で機能します。energy-エネルギーが書き込まれる配列とsum-合計が書き込まれる配列。

すでにこの配列を持っているので、考える時が来ました-なぜそれが必要なのでしょうか？私は答えます-この配列から、エネルギーの合計が最小のチェーンをすばやく見つけることができます。

まず、画像の一番下の行のどのピクセルがこのチェーンに属しているかを見つけます。探している要素は、一番下の行の要素の中でsum配列で最小の値を持ちます。なんで？この配列では、上端から指定されたピクセルまでの最小チェーンの要素の合計の値が記録されることを思い出してください。興味のあるチェーンは、最後の行のピクセルで終了します。したがって、図全体について、最小チェーンは、最終行からピクセルで終わるすべての最小チェーンの最小として選択されます。

この例では、これは次の要素になります。

最小チェーンが終了するピクセルはすでにわかっていますが、最後から2番目の行からピクセルを見つけることができます。すでに説明したように、下のピクセルから、上の行にある3つの隣接ピクセル（左上、上、または右上）にのみ移動できます。これらのピクセルの中から、合計配列の最小値を持つピクセルを選択して、そこに移動します。トップラインに達するまで続けます。次の図にプロセスを示します。

これらすべての操作を完了すると、必要なもの、つまり画像の損失を最小限に抑えながら変更できるピクセルのセットが得られます。

図の最小チェーンの例：

チェーン検索アルゴリズムのソフトウェア実装：

 private int[] FindShrinkedPixels() { //    int last = imgHeight - 1; //      int[] res = new int[imgHeight]; //     sum,          res[last] res[last] = 0; for (int j = 1; j < imgWidth; j++) if (sum[last, j] < sum[last, res[last]]) res[last] = j; //         . for (int i = last - 1; i >= 0; i--) { // prev -       //         (prev-1), prev  (prev+1),      int prev = res[i + 1]; //   ,     sum,  ,    ,        res[i] res[i] = prev; if (prev > 0 && sum[i, res[i]] > sum[i, prev - 1]) res[i] = prev - 1; if (prev < imgWidth - 1 && sum[i, res[i]] > sum[i, prev + 1]) res[i] = prev + 1; } return res; }

図面の削減

最終的に、作業に使用するピクセルのチェーンを見つけました。今、私たちが彼女を探していた理由を思い出すことができます。私たちの仕事は画像のサイズ変更です。画像の拡大と縮小はわずかに異なるため、最初に縮小を検討し、次に拡大を検討します。

画像の幅を1ピクセル減らす必要がある場合、すべてが簡単です。上で説明したように、垂直チェーンを見つけて、画像から削除するだけです。次のループでこの操作を実装しました。

 for (int i = 0; i < imgHeight; i++) for (int j = cropPixels[i]; j < imgWidth; j++) { pImage[i, j] = pImage[i, j + 1]; }

cropPixels配列のi番目の要素には、ピクセル列の番号が書き込まれ、i番目の行から削除されます。サイクル自体は次のことを行います。削除するピクセルの右側に書き込まれるすべてのピクセルは、1ポイント左にシフトします。この操作の結果、ピクセルチェーンは画像から削除されます。

イメージを1ピクセルではなく、より大きな値で縮小する必要がある場合は、必要に応じてチェーンを削除する操作を実行します（このチェーンを探す必要があるたびに）。

画像をnピクセル縮小する操作と、画像を1ピクセルn回縮小する操作は同等ではないことに注意してください。それらの違いは、1ピクセルずつn倍に減らすと、各中間画像についてピクセルのエネルギーを探し、すぐにnだけ減らすと、元の画像からピクセルのエネルギーを取り出すことです。

図面の拡大

画像を縮小する方法はすでにわかっていますが、今は画像を拡大する方法を見つける必要があります。

最初に頭に浮かぶのは、チェーンを選択し、チェーンを選択して「ストレッチ」するときとまったく同じです。しかし、これを実装すると、次の結果が得られます。

ご覧のとおり、プログラムは1列だけを引き伸ばしていますが、これは必要なものではありません。

たとえば、次のような考えが考えられます。最小チェーンを1つではなく、必要な幅に合わせて画像を完成させるのに必要なだけの量を取る必要があります。このアルゴリズムを実装したとしますが、図を2倍にするとどうなりますか？

この図からわかるように、すべてのポイントを選択して水平方向にストレッチしましたが、この方法は通常のストレッチと変わらないため、必要なものではありません。

しかし、原則として、後者の方法のアイデアそのものは正しいですが、わずかな変更があります。段階的に画像を拡大する必要があります。そのため、各段階で画像の「重要ではない」部分をできるだけ多く、「重要な」部分をできるだけ少なくします。その後、増加するプロセスを段階的に分割する方法が問題になりますか？手動で段階に分割することから、ある種のヒューリスティックアナライザーを作成することまで、多くのオプションがあります。しかし、私のプログラムでは、簡単に記述しました。段階への分割は、各段階で画像が50％を超えて増加しないように行われます。これは受け入れられる結果になる場合もありますが、そうでない場合もありますが、既に書いたように、ステージへの分割を実装するための多くのオプションを考え出すことができます。

この方法でUFO画像を拡大すると、次の結果が得られます。