PageRankの最終結果はPRページの「重要性」の特定の指標であり、PR0からPR10の値を取り、着信リンクを分析することで計算されることは誰もが知っています。 その量と質は、オンラインコミュニティにとってこのページの重要性を示しています。
表示されるPRレベルは非常に丸められた値であり、正確なインジケーターはGoogleプログラマーのみが知っています。 PR指数は対数スケールで変化します。つまり、PR5の値はPR4よりも1桁大きくなります。
PRの計算に使用される式は何ですか？ これについては、American Mathematical SocietyのWebサイトの詳細な記事で説明されています。
PageRankの仕組みは次のとおりです。 ページPjにljリンクがあるとします。 これらのリンクのいずれかがページPiにつながる場合、Pjはその「重要度」の1 / ljをページPiに渡します（カルマの「ハブレ」への転送はほぼ同じ方法で機能します）。
Piページの重要度レベル（PR）は、すべての着信リンクからのそのようなすべての値の合計です。 PiページにBiとしてリンクする一連のページを想像すると、Piの「重要度」は次の式を使用して計算されます。
これはすべて、鶏と卵の問題のように見えます。 PRページを見つけるには、まず、それにリンクしているすべてのページのPRを知る必要があります。 ただし、数学的な方法でこの問題を解決できます。
このために、ハイパーリンクのマトリックスが作成されます。
、列jの行iの形式は次のとおりです。
これは、確率的行列、つまり、すべての列および/または行が非負の実数の行であり、合計で1である行列です。
ベクトルを形成します
その要素はPR値、つまり、すべてのページの「重要性」です。 条件に従って、ベクトルは静止しています。
8つのWebページの小さなマトリックスの例を使用して状況を考えてみましょう。その間のハイパーリンクは矢印で表示されます。
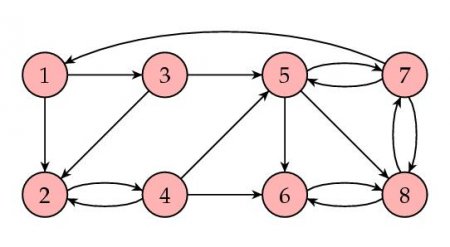
この状況はそのような行列に対応します
および定常ベクトル
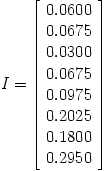
計算では、ページ8が人気コンテストに勝つことが示されています。 これは、最も「信頼できる」ページが明るい色でペイントされている同じ写真です。
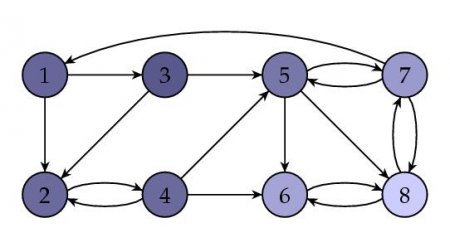
これが、数学的な観点から見たPageRankの仕組みです。 これらは、アルゴリズムの基本原則にすぎません。 詳細は、 元の記事に記載されています 。