量子化学の観点からのミュオン触媒作用。 パートII：電子対 ミューオン化学結合

Mnogabukaffは、量子化学がミューオン触媒の動作原理、つまりミューオンが所望のプラズマの温度をいかに正確に下げるかについて考えている。 2つの部分（最初の部分はここで読むことができます ）。



2番目の部分の本質は単純です。ミューオンは電子よりも重いため、化学結合が強くなり、核の収束が大きくなり、熱核反応を起こすために必要なプラズマ温度が下がります。



しかし、式、グラフを見て、最も単純な（準）分子に適用される量子化学の概念的な本質を見たい人は、catの下で歓迎します。

はじめに

最初の部分（ ここを参照）では、水素原子と $$$\ mathrm {H} ^ \ cdot = \ mathrm {p ^ + e ^-}$ その重いミューオンの対応物から $$$\ mathrm {p} ^ + \ mu ^-$ ：2番目の場合、ミューオンはより強く結び付けられ、陽子からより近い距離に位置します。 同時に、ここで必要となるいくつかの重要な事柄（軌道の形式と単位の原子系）を調べました。



2番目の部分（つまり、ここ）では、熱核反応に点火するために必要なプラズマ温度が低下する理由、方法、および程度を理解しようとします。 私たちが興味を持っている反応は次のとおりです。

$$

$$\ mathrm {{} ^ nH + {} ^ m H \ rightarrow} \ \ text {新しいカーネル+エネルギー}$$

ここで、n、m = 1,2,3は、それぞれプロトン、重水素、トリチウムに対応します。 当然、これらの原子核は正の電荷を持っているため、それらを近づけようとすると、クーロンの法則に従って反発し始めます（ 前のセクションを参照）。これは、熱核融合反応の開始を妨げる非常に障壁です。 ところで、核崩壊反応の場合、この反発には逆の役割があります。なぜなら、共通の核から離れた後、フラグメントは互いに反発し、追加の運動エネルギーを獲得し、このエネルギーが原子力発電所で加熱されるからです。



このクーロン障壁を克服するには、プラズマ温度（ T ）の上昇が必要です。これは、誰もがMKTの学校のコースで覚えているように、プラズマの平均粒子速度（ v ）

$$

$$mv ^ 2 = 3k_ \ mathrm {B} T$$

ここで、 mは粒子の質量です。 $$$k_ \ mathrm {B}$ - ボルツマン定数 。



しかし、2つの水素原子核を特定の粒子に結合し、それらが既に近くに配置されているため、それらの障壁の残りの部分は既に非常に小さいと考えてみましょう。 次に、これらの粒子を組み合わせて新しいものにするために、これらの粒子を大幅に加速する必要があります（読む：低温が必要です）。 そして、まさにそのような役割は中間的なイオンを演じるべきです $$$（\ mathrm {{} ^ nH} \ mu ^-\ mathrm {{} ^ mH}）^ +$ 、水素分子のイオンの類似体 $$$\ mathrm {H} _2 ^ + =（\ mathrm {He ^ -H}）^ +$ 。

これら2つの粒子の違いを調べて、熱核融合の発火温度を下げるのにミューオンがどれほど効果的であるかを理解します。

MILK MO LKAOメソッド

したがって、電荷+ e （1電子電荷モジュロ）を持つ2つの水素原子核と電荷-eを持つ1つの粒子（電子またはミューオン）で構成される分子システムがあります。 私たちのシステムは、他の粒子と衝突するまで分離されているため、そのエネルギーは構成要素に分解できます。

$$

$$E = T（\ mathrm {H} _1）+ T（\ mathrm {H} _2）+ \アンダーブレース{T（\ mathrm {e} ^-/ \ mu ^-）+ V（\ mathrm {H_1 \ text {from} H_2}）+ V（\ mathrm {\ mathrm {e} ^-/ \ mu ^-\ text {} \ mathrm {H} _1}）+ V（\ mathrm {\ mathrm {e} ^- / \ mu ^-\ text {k} \ mathrm {H} _2}）} _ {E_ \ mathrm {e}}$$

ここで、最初の2つの用語（ $$$T（\ mathrm {H} _1）$ そして $$$T（\ mathrm {H} _2）$ ）水素原子核の運動エネルギー、第3項（ $$$T（\ mathrm {e} ^-/ \ mu ^-）$ ）負の粒子（電子またはミューオン）の運動エネルギー、第4項 $$$V（\ mathrm {H_1 \ text {from} H_2}）$ 相互からの水素のクーロン反発のエネルギーであり、残りの2つは、各プロトンへの電子/ミューオンのクーロン引力です。 一般的な場合、これは3体問題であり、単なる量子問題です。 当然、額でそれを解決することは非常に困難です。 しかし、幸いなことに、原子核は電子よりも少なくとも1800倍重く、ミューオンよりも10重重いため、小さな負の粒子よりも明らかに遅く移動します。 このため、最初に問題を解決することができます。最初に、核の動きに関係しない運動のエネルギーを見つけます。 $$$E_ \ mathrm {e}$ そして完全なエネルギー。 こんな感じです。

1. 互いに対する水素原子核の配置が選択され、これにより、水素原子核と電子/ミューオンとのクーロン相互作用が決まります。 クーロンポテンシャル $$$V（R）= k \ frac {q_1q_2} {R}$ 粒子電荷のみに依存 $$$q_i$ したがって、それらの間の距離は、すべての水素同位体について、この値は同じになります。 次に、これらの核の分野における電子/ミューオンの運動の問題が解決されます。 これは1つの団体の仕事です。
2. これらのエネルギー $$$E_ \ mathrm {e}$ 相互の相対的な原子核のすべての可能な配置に対して計算され、これは原子核の運動の有効ポテンシャルエネルギーになります。 この場合、相互に異なる距離でエネルギーを計算する必要があるため、核のペアのポテンシャルは常に1次元です。 それでは、2つの水素同位体の相対運動の2体問題を解くだけで十分です。

明らかに、私たちの問題の根源は、原子核の分野での電子/ミュー粒子エネルギーの計算です $$$E_ \ mathrm {e}$ 。 実際、これは化学結合です。特定の場所で核を一緒に保持する特定のポテンシャルです。 そして、化学結合のエネルギーを見つけるこのまさにタスクは、量子化学の主要なタスクです。



残念ながら、ミュー粒子と電子は両方とも量子粒子です。したがって、このエネルギーを見つけるには、量子力学の方法に頼らなければなりません。 実際、2つの同一核の場での電子/ミューオンの運動の問題は明示的に解決されていますが（ ここを参照）、この解決策は非常に複雑であり、結果は水素のような原子の場合ほど明確ではありません。 したがって、すべてのシステムに適用できる別の近似アプローチを分解しようとします。 これはいわゆる 原子軌道の線形結合としての分子軌道法、またはMO LKAO。



水素原子核の分野での電子/ミューオンの運動に関するシュレディンガー方程式を詳しく見てみましょう。

$$

$$\ hat {H} \ psi = \ underbrace {\ left（\ overbrace {-\ frac {1} {2m}（\ frac {\ partial ^ 2} {\ partial x ^ 2} + \ frac {\ partial ^ 2} {\ partial y ^ 2} + \ frac {\ partial ^ 2} {\ partial z ^ 2}）} ^ {\ hat {T}} + \ overbrace {-\ frac {1} {R_1}} ^ {\ hat {V} _1} + \ overbrace {-\ frac {1} {R_2}} ^ {\ hat {V} _2} + \ overbrace {\ frac {1} {R}} ^ {\ hat {V } _ \ mathrm {HH}} \ right）} _ {\ hat {H}} \ psi = E \ psi$$

この方程式は、原子の単位系で記述されています（ 前のPSを参照）。したがって、水素原子核と電子/ミューオンの電荷はそれぞれ+ 1、-1、電子質量はm = 1、ミューオンの場合は ≈207です。



さらに詳しく見ると、ハミルトニアンでは、水素原子のハミルトニアンである核の1つだけの周りの負の粒子の動きに純粋に関連する部分を選択できることに気付くことができます。これは2つの方法で実行できます。

$$

$$\ hat {H} =（\オーバーブレース{\ hat {T} + \ hat {V} _1} ^ {\ hat {H} _ {1}} + \ hat {V} _2 + \ hat {V} _ \ mathrm {HH}）=（\オーバーブレース{\ hat {T} + \ hat {V} _2} ^ {\ hat {H} _ {2}} + \ hat {V} _1 + \ hat {V} _ \ mathrm {HH}）$$

水素様原子のハミルトニアン外（ $$$\ hat {H} _i、\ i = $ 1.$ ）電子/ミューオンと別の核との相互作用のエネルギー（ $$$\ hat {V} _j$ ）および核反発エネルギー（ $$$\ hat {V} _ \ mathrm {HH}$ ） それらの2番目は電子の動きにまったく影響を与えません-それはエネルギーの一定量のシフトだけですが、電子と別の核との相互作用は重要なことです。

粒子はいつでも核の1つだけで回転し、2番目の核との相互作用は単なる修正であると想像できます。 核の1つを中心とした回転の方法として、電子/ミューオンが基底（1s）状態にあると仮定できます。その波動関数は前の部分からよく知られています。

$$

$$| 1s \ rangle = \ frac {1} {\ sqrt {\ pi}} \ exp \左（-\ frac {R} {R_1} \右）$$

どこで $$$R_1$ 粒子のボーア半径です。 電子の場合 $$$R_1 = 1$ ホウ素（電子のボーア半径、約0.5オングストロームに等しい）、およびミューオンの場合 $$$R_1 = \ frac {1} {m_ \ mu} \約\ frac {1} {207}$ 。

どういうわけか2つの原子核の場の電子/ミューオン波動関数を近似するために、次の表現を試すことができます。

$$

$$\ psi \およそc_1 | 1s_1 \ rangle + c_2 | 1s_2 \ rangle$$

そして、私たちと一緒に複雑な偏微分方程式を解くタスクは、2つの未知の係数c ₁とc ₂を探すことになります 。 これは、係数（科学の線形結合）原子1 s軌道との合計として表される非常に分子軌道です。



当然、これらのパラメーターの方程式が必要です。 そして、この近似をシュレディンガー方程式に代入すれば、それを得るのは非常に簡単です $$$\ hat {H} \ psi = E \ psi$ ：

$$

$$\ hat {H}（c_1 | 1s_1 \ rangle + c_2 | 1s_2 \ rangle）= c_1 \ hat {H} | 1s_1 \ rangle + c_2 \ hat {H} | 1s_2 \ rangle = E（c_1 | 1s_1 \ rangle + c_2 | 1s_2 \ rangle）= c_1 E | 1s_1 \ rangle + c_2 E | 1s_2 \ rangle$$

実際、この比率はどこでも満たされるようにしたいので、このすべての平均値を何らかの方法で計算できます。 左のこの式に乗算します $$$<1s_1 |$ そして $$$<1s_2 |$ すべての座標を統合します。 結果として、係数c ₁ 、 c ₂およびエネルギーEを見つける必要がある2つの線形方程式のシステムを取得します。

$$

$$\ begin {pmatrix} \ langle 1s_1 | \ hat {H} | 1s_1 \ rangle＆\ langle 1s_1 | \ hat {H} | 1s_2 \ rangle \\ \ langle 1s_2 | \ hat {H} | 1s_1 \ rangle＆\ langle 1s_2 | \ hat {H} | 1s_2 \ rangle \\ \ end {pmatrix} \ begin {pmatrix} c_1 \\ c_2 \ end {pmatrix} = E \ begin {pmatrix} \ langle 1s_1 | 1s_1 \ rangle＆\ langle 1s_1 | 1s_2 \ rangle \\ \ langle 1s_2 | 1s_1 \ rangle＆\ langle 1s_2 | 1s_2 \ rangle \\ \ end {pmatrix} \ begin {pmatrix} c_1 \\ c_2 \ end {pmatrix}$$

線形代数を研究した人は誰でも、一般化された固有ベクトル固有値問題を認識するでしょう。 それを解く前に、2つの行列の要素が何であるかを分析します。それらはそこにあります（同時に、1文字でそれらの短い指定を紹介します）。

• 最も単純なものから始めましょう： $$$\ langle 1s_1 | 1s_1 \ rangle = \ langle 1s_2 | 1s_2 \ rangle = 1$ -これは波動関数の正規化であり、私たちが思い出すように、電子/ミューオンを見つける合計確率はどこかで少なくとも1です。
• $$$\ langle 1s_1 | 1s_2 \ rangle = \ langle 1s_2 | 1s_1 \ rangle = S$ -これはいわゆる オーバーラップ積分。各原子の1s電子雲がどのようにオーバーラップするかを示します。
• $$$\ langle 1s_1 | \ hat {H} | 1s_1 \ rangle = \ langle 1s_2 | \ hat {H} | 1s_2 \ rangle = \ alpha$ 。 この積分は、いくつかの部分で構成されています。
  
  
  
  
  
  
  

  $$

  $$\ langle 1s_1 | \ hat {H} | 1s_1 \ rangle = \ underbrace {\ langle 1s_1 | \ hat {H} _1 | 1s_1 \ rangle} _ {-\ frac {m} {2}} + \ langle 1s_1 | \ hat {V} _2 | 1s_1 \ rangle + \ frac {1} {R}$$
  
  
  
  
  
  
  
• $$$\ langle 1s_1 | \ hat {H} | 1s_2 \ rangle = \ langle 1s_2 | \ hat {H} | 1s_1 \ rangle = \ beta$ 。 ここでは似ています：
  
  
  
  
  
  
  

  $$

  $$\ langle 1s_2 | \ hat {H} | 1s_1 \ rangle = \ underbrace {\ langle 1s_2 | \オーバーブレース{\ hat {H} _1 | 1s_1 \ rangle} ^ {-\ frac {m} {2} | 1s_1 \ rangle}} {{\ frac {m} {2} S} + \ langle 1s_2 | \帽子{V} _2 | 1s_1 \ rangle + \ frac {S} {R}$$
  
  
  
  
  
  
  つまり オーバーラップ積分（最初と最後の項）でスケーリングされた水素様原子と核間反発のエネルギー、および、ある原子から別の原子へホッピングする電子/ミューオンのエネルギー。
  
  

次のように書き換えられた方程式から、水素様イオンのエネルギーの式を見つけましょう。

$$

$$\ begin {pmatrix} \ alpha＆\ beta \\ \ beta＆\ alpha \ end {pmatrix} \ begin {pmatrix} c_1 \\ c_2 \ end {pmatrix} = E \ begin {pmatrix} 1＆S \\ S ＆1 \ end {pmatrix} \ begin {pmatrix} c_1 \\ c_2 \ end {pmatrix}$$

エネルギーを見つけるには、方程式を解く必要があります。

$$

$$\ det \ begin {pmatrix} \ alpha -E＆\ beta -ES \\ \ beta-ES＆\ alpha -E \ end {pmatrix} =（\ alpha -E）^ 2-（\ beta-ES）^ 2 = 0$$

ここで、「det」は行列式（ロシア語では行列の行列式）を示します。



Eに関するこの2次方程式の解は次のとおりです。

$$

$$E_ \ pm = \ frac {\ alpha \ pm \ beta} {1 \ pm S} =-\ frac {m} {2} + \ frac {1} {R} + \ frac {\ langle 1s_1 | \ hat {V} _2 | 1s_1 \ rangle \ pm \ langle 1s_2 | \ hat {V} _2 | 1s_1 \ rangle} {1 \ pm S}$$

最初の部分は明らかに原子のエネルギー、2番目は核間反発、熱核反応の発火を防ぐ同じクーロン障壁であり、最後の複雑な構造に対処する必要があります。



電子/ミューオンエネルギーの単なる基準点である核間反発を破棄すると、エネルギーを持つ2つの状態があることがわかります

$$

$$\ epsilon_ \ pm =-\ frac {m} {2} + \ frac {\ langle 1s_1 | \ hat {V} _2 | 1s_1 \ rangle \ pm \ langle 1s_2 | \ hat {V} _2 | 1s_1 \ rangle} {1 \ pm S}$$

両方の波動関数 $$$| 1s_1 \ラングル$ そして $$$| 1s_2 \ラングル$ -ポジティブ、そして $$$\ hat {V} _i <0$ （負の粒子は常に正に引き寄せられるため）、その後 $$$\ epsilon_ + <-\ frac {m} {2}$ （単一原子のエネルギー）、および $$$\ epsilon _->-\ frac {m} {2}$ 、つまり 分子軌道の標準的な画像を取得します。







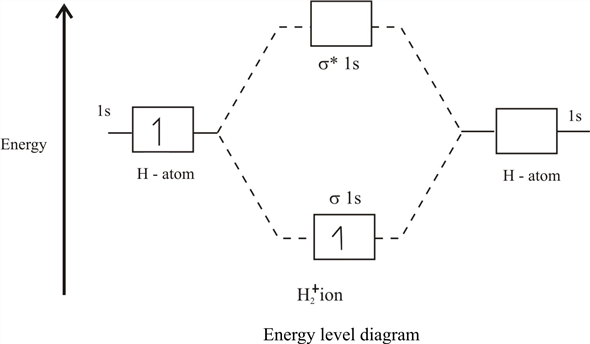
エネルギーを伴う低軌道 $$$E _ +$ バインディングと呼ばれ、トップ（エネルギーを持つ $$$E _-$ ）-結合防止、またはゆるみ。 その結果、電子/ミューオンが低分子軌道上にある場合、1個の周りよりも2個の原子核の周りを飛行することで恩恵を受け、その運動によりシステムの全エネルギーが低下します。 そして、これは核間反発を遮断する非常に魔法の化学結合であり、核がかなりの時間にわたって互いに隣り合うことを可能にします。



そして、水素原子核がどれだけ接近できるかを理解するために、化学結合の積分を計算する必要があります。 実際、求められている3つの積分はすべて分析的に計算されていますが、それはひどくhemoで複雑です（興味のある方は、 フラリーの本「Quantum Chemistry」の第9章を参照してください）。 したがって、別の方法でより簡単に進み、モンテカルロ法を使用してこれらの積分を数値的に計算します。

メトロポリス法

熱核エネルギーに関するテキストでは、彼女の祖父である軍事原子、より具体的にはマンハッタンプロジェクトに敬意を表するのは非常に論理的だと思います。 モンテカルロ法が成長したのは彼からであり、特に、著者の一人であるエドワード・テラーが「水素爆弾の父」であるメトロポリスアルゴリズム （つまり、Envetok環礁で熱核融合を開始した人）です。





一般に、メソッドの本質を分析します。 統計力学のタスクを対象としています。 その中の主な分布はボルツマン分布です：特定の状態でシステムを検出する確率は $$$\ exp（-\ベータE）$ 、 $$$\ beta ^ {-1} = k_ \ mathrm {B} T$ 。 そして、熱力学的平衡にあるシステムのパラメーターAの観測値は、積分に等しい

$$

$$\ langle A \ rangle = \ frac {1} {Z} \ int A（q）\ exp（-\ beta E（q））dq$$

ここで、 qはシステムの状態をパラメーター化する座標（たとえば、粒子の座標/運動量）、 Zはパーティション関数と呼ばれる正規化係数です。

$$

$$Z = \ int \ exp（-\ beta E（q））dq$$

システムに非常に多くの粒子が存在する場合、額の積分をまったくカウントすることは完全に非現実的です。 単純にランダムなq座標の束を選択する単純なモンテカルロ法でも、確率が実際に可能なシステムの状態がある場合、意味のあるものは何も得られません。 $$$\ exp（-\ベータE）$ 著しくゼロ以外、ごくわずかです。 そして、そのような場合のために、重要度によるサンプリングが必要です。この場合、アルゴリズムは、状態空間の十分に確率の高い場所のみをサンプリングできます。



Metropolisアルゴリズムは次のようになります。

1. シミュレーションを開始するとき、構成空間でいくつかの開始近似値を選択します $$$\ mathbf {q} ^ {（0）}$ 可能な最大増分のベクトル $$$\ delta \ mathbf {q}$ 。 開始点で、システムのエネルギーを計算します $$$E ^ {（0）} = E（\ mathbf {q} ^ {（0）}）$ （読み取り-確率 $$$p = \ exp（-\ beta E ^ {（0）}）$ ）
2. n番目のステップでの新しい構成は次のとおりです。
   
   
   1. トライアル構成のエネルギーを計算します $$$E_ \ mathrm {トライアル} = E（\ mathbf {q} _ \ mathrm {トライアル}）$ （すなわち、確率 $$$p_ \ mathrm {trial} = \ exp（-\ beta E_ \ mathrm {trial}）$ ）
   2. そして、古い確率を比較します $$$p ^ {（n）}$ トライアル付き $$$p_ \ mathrm {トライアル}$
      
      
      
      
      • 新しい構成の確率がより大きいか同じ場合（ $$$\ frac {p_ \ mathrm {trial}} {p ^ {（n）}} \ geq 1$ ）、または同等に、新しいポイントのエネルギーは古いポイントのエネルギーよりも低いか同じです（ $$$E_ \ mathrm {トライアル} \ leq E ^ {（n）}$ ）、新しいポイントが受け入れられ、システムがそのポイントに入ります（ $$$q ^ {（n + 1）} = q_ \ mathrm {トライアル}$ ）、
      • トライアル構成のエネルギーが高い場合（ $$$E_ \ mathrm {トライアル}> E ^ {（n）}$ ）、これは同等です $$$\ frac {p_ \ mathrm {trial}} {p ^ {（n）}} <1$ 、この場合、乱数を生成します $$$P \ in [0; 1）$ 均一な分布から、遷移確率である確率の比率と比較します。 もし $$$P <\ frac {p_ \ mathrm {trial}} {p ^ {（n）}}$ 、その後、新しいポイントを受け入れ、そうでない場合（ $$$P \ geq \ frac {p_ \ mathrm {trial}} {p ^ {（n）}}$ ）、拒否します。システムは古い構成のままです（ $$$q ^ {（n + 1）} = q ^ {（n）}$ ）...
      
      
      
   
   
   
3. 上記のアルゴリズムに従って多くのステップを踏んで、システム構成の可能なスペースの重要な（つまり、本当に重要な）部分をサンプリングします。 関心のある積分は、次の式で計算されます。
   
   $$$\ langle A \ rangle = \ frac {1} {Z} \ int A（\ mathbf {q}）\ exp（-\ beta E（\ mathbf {q}））d \ mathbf {q} = \ frac { 1} {N} \ sum_ {n = 0} ^ {N} A（\ mathbf {q} ^ {（n）}）$
   
   

これがMetropolisアルゴリズムの仕組みです。



そして今、私たちが興味を持っている3つの積分の計算にそれを適応させる必要があります。 それらをさらに詳しく見てみましょう。

• $$$S（R）= \ langle 1s_2 | 1s_1 \ rangle = \ int \ limits _ {-\ infty} ^ {+ \ infty} \ int \ limits _ {-\ infty} ^ {+ \ infty} \ int \ limits _ {- \ infty} ^ {+ \ infty} \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp（-m \ underbrace {| \ mathbf {r}-\ mathbf {r} _2 | } _ {R_2}）} _ {1s_2}} ^ {A（\ mathbf {r}）} \ cdot \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp（-m \下括弧{| \ mathbf {r}-\ mathbf {r} _1 |} _ {R_1}）} _ {1s_1}} ^ {p（\ mathbf {r}）} dx dy dz$ どこで $$$\ mathbf {r} =（x、y、z）^ \ mathbf {T}$ -電子/ミューオンの座標、 $$$\ mathbf {r} _i =（x_i、y_i、z_i）^ \ mathbf {T}$ 水素原子核の座標であり、 $$$R_i = | \ mathbf {r}-\ mathbf {r} _i | = \ sqrt {（x-x_i）^ 2 +（y-y_i）^ 2 +（z-z_i）^ 2}$ -正と負の粒子間の距離、
  
  
• $$$\ langle 1s_1 | \ hat {V} _2 | 1s_1 \ rangle =-\ int \ limits _ {-\ infty} ^ {+ \ infty} \ int \ limits _ {-\ infty} ^ {+ \ infty} \ int \制限_ {-\ infty} ^ {+ \ infty} \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp（-mR_1）} _ {1s_1} \ frac {1} {R_2} } ^ {A（\ mathbf {r}）} \ cdot \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp（-mR_1）} _ {1s_1}} ^ {p（\ mathbf {r}）} dxdydz$
• $$$\ langle 1s_2 | \ hat {V} _2 | 1s_1 \ rangle =-\ int \ limits _ {-\ infty} ^ {+ \ infty} \ int \ limits _ {-\ infty} ^ {+ \ infty} \ int \制限_ {-\ infty} ^ {+ \ infty} \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp（-mR_2）} _ {1s_2} \ frac {1} {R_1} } ^ {A（\ mathbf {r}）} \ cdot \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp（-mR_1）} _ {1s_1}} ^ {p（\ mathbf {r}）} dxdydz$

確率pに対して原子の1つの1s関数を計算すると、





積分の符号の下にある他のすべて（2番目の波動関数と3分の2の場合、電子/ミューオンの核への引力の可能性）は、平均値が計算される関数になります。 メトロポリス法による通常の計算とは対照的に、行わなければならない唯一のことは、積分の正規化をまっすぐにすることです。 事実は、標準の正規化がオンになるということです

$$

$$Z = \ int \ limits _ {-\ infty} ^ {+ \ infty} \ int \ limits _ {-\ infty} ^ {+ \ infty} \ int \ limits _ {-\ infty} ^ {+ \ infty} \ exp （-m R）dx dy dz = 4 \ pi \ int \ limits_ {0} ^ {+ \ infty} \ exp（-m R）R ^ 2 dR = \ frac {8 \ pi} {m ^ 3}$$

そして、正規化が必要です $$$\ sqrt {\ langle 1s_1 | 1s_1 \ rangle}$ どこで

$$

$$\ langle 1s_1 | 1s_1 \rangle = \int \limits_{-\infty}^{+\infty} \int \limits_{-\infty}^{+\infty} \int \limits_{-\infty}^{+\infty} \exp(-2 m R) dx dy dz = 4 \pi \int \limits_{0}^{+\infty} \exp(-2m R) R^2 dR = \frac{\pi}{m^3}$$

これは、メトロポリスに従って計算された各積分に係数を掛ける必要があることを意味します

$$

$$\frac{Z}{\sqrt{\langle 1s_1 | 1s_1 \rangle} } = 8 \sqrt{\frac{\pi}{m^3}}$$

これは、たとえばPythonなどの特定のスクリプトの形式で既に編成できます（たとえば、以下のコードです）。





このような計算を使用して、水素イオンのポテンシャルエネルギーを最終的に比較できます。 $$$\ mathrm {H} _2 ^ +$ そしてそのミューオンの対応物。

$$$\ mathrm {H_2 ^ + = p ^ + e ^-p ^ +}$ 対 $$$\ mathrm {p ^ + \ mu ^-p ^ +}$

そのため、スクリプトを使用して、電子とミューオンによって結合された水素原子核の接近のポテンシャルエネルギーの表面を計算できます。 エネルギーの基準点として、互いに無限に希釈された原子を取ります（つまり、 $$$-m / 2$ 、これは核間の距離でのポテンシャルに等しい $$$R = + \ infty$ ）



電子の場合、最小値に近い電位は次のようになります。







最小値は約2ボロンの距離（つまり、約2原子半径の合計）で発生し、分子のフラグメントへの解離エネルギーは約0.06ハートリーであり、これは約20,000ケルビン（または摂氏、ここでは問題ありません）までの加熱に対応します。 エネルギーを変換するには、 このようなオンラインリソースの使用をお勧めします。



ミューオン的に結合した水素イオンの同様の状況：







ミューオン水素のボーア半径は小さいため（ 前のパートを参照）、水素原子核も最小ポテンシャルエネルギーで約200倍近くに位置します。 この分子の破壊エネルギーはすでに10 Hartreeを超えており、これは3リャム度（ $$$\約（3.2 \ cdot 10 ^ 6）^ \ circ$ ）



点火のために、反応には通常10 ⁸ Kのオーダーの温度が必要です 。これは約320ハートリーです。 通常のディボドロンイオンの場合とそのミューオンバージョンの場合に、同様のエネルギーがどの距離で達成されるかを見てみましょう。







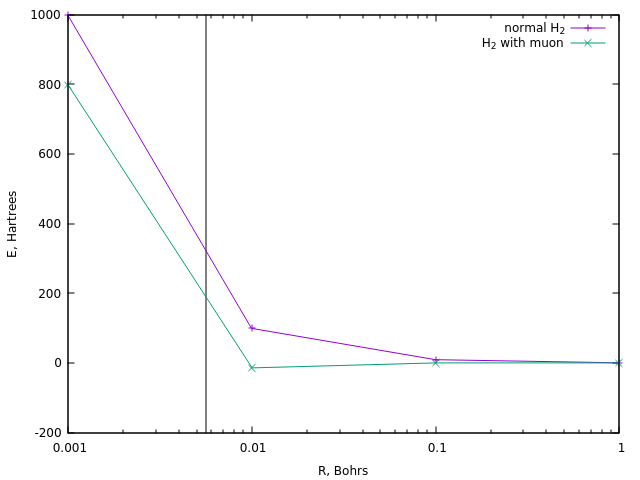
前者の場合、これは約0.0058ボロン（垂直線）の距離に対応します。



ミューオン水素の同様の距離は、約190 Haのエネルギーで達成されます。 約1.5倍少ない。 そして、これはミューオン触媒の温度の最も簡単な推定値です。



しかし実際には、すべてがさらにクールになります。 事実、安定した粒子が形成される場合 $$$\ mathrm {（{} ^ mH（\ mu ^-）{} ^ nH）^ +}$ 、これらの核は、ミューオンが生きている間、互いに対して振動します。 そして、ここで「2つの水素原子」状態から「より重い核」状態へのトンネリングが発生する可能性があり、トンネリングの確率は必要なトンネリング長dにほぼ依存します。 $$$p ^ {-d}$ そのため、ミューオンによって2つの原子核を近づけることにより、この反応がトンネリングする確率を大幅に高めることができます。 残念ながら、この効果の推定には量子化学は不要になりましたが、核物理学は不要になったため、議論のこの部分はこの投稿の範囲外です。 これで停止します。

PSなぜそれほど単純ではないのですか？

実際、これらの粒子を形成することは、プラズマ条件ではそれほど単純ではありません。 実際には、2つの粒子が衝突すると、それらの全エネルギーは明らかに解離（または核+電子/ミューオンの場合はイオン化）のエネルギーを超えるため、衝突すると安定した粒子（原子、イオン、分子）を形成せずに飛行しますお互いを過ぎて。 互いに固執するためには、余剰エネルギーをどこかで捨てる必要があります。そのためには、このエネルギーを引き受ける3人目の余分な人が必要です。 それは光子、または近くを飛んでいるある種の左の粒子である可能性がありますが、主なことは、条件がこの過剰エネルギーの同伴に寄与するべきであるということです。

PPS

コメント/説明/質問がある場合は、コメントまたはPMに記入してください。 すべてを修正し、すべてに答えて説明します。