
前回の投稿では、「岩の上を歩く」という問題を提示し、意味のないひどいアルゴリズムに落ち着きました。 今回は、この灰色のボックスの秘密を明らかにし、まったく怖くないことを確認します。
まとめ
将来の報酬の量を最大化することにより、目標への最速パスも見つけられると結論付けたため、現在の目標はこれを行う方法を見つけることです!
Qラーニングの概要
- ある状態で特定のアクションがどれだけうまく実行されるかを測定するテーブルを作成することから始めましょう(単純なスカラー値で測定できるため、値が大きいほどアクションが良くなります)
- このテーブルには、状態ごとに1行、アクションごとに1列があります。 私たちの世界では、グリッドには48(Y x 4 x 12 x X)の状態があり、4つのアクション(上、下、左、右)が許可されているため、テーブルは48 x 4になります。
- このテーブルに保存される値は「Q値」と呼ばれます。
- これらは、将来の報酬の額の見積もりです。 言い換えれば、彼らはゲームが終了する前にどれだけ多くの報酬を得ることができるかを推定し、状態SにいてアクションAを実行します。
- ランダムな値(またはすべてのゼロなどの定数)でテーブルを初期化します。
最適な「Qテーブル」には、各州で最高の行動を取ることができる値があり、最終的に勝つための最良の方法を提供します。 問題は解決されました、歓声、ロボット君たち:)。
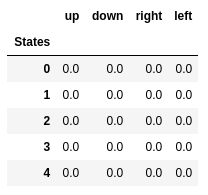
最初の5つの状態のQ値。
Qラーニング
- Qラーニングは、これらの値を「学習」するアルゴリズムです。
- すべてのステップで、私たちは世界に関するより多くの情報を取得します。
- この情報は、テーブルの値を更新するために使用されます。
たとえば、ターゲットから1ステップ離れている(正方形[2、11])とし、下がった場合、-1ではなく0の報酬が得られるとします。
この情報を使用して、テーブル内の状態とアクションのペアの値を更新できます。次回アクセスしたときに、下に移動すると0の報酬が得られることが既にわかっています。
これで、この情報をさらに広めることができます! 正方形[2、11]からゴールへのパスがわかったので、正方形[2、11]につながるアクションも良好になります。したがって、正方形のQ値を更新し、[2、11]に導きます。 0に近づきます。
そして、それは皆さん、Qラーニングの本質です!
目標に到達するたびに、目標を達成する方法の「マップ」を1マスずつ増やすため、十分な数の反復の後、各状態から目標に到達する方法を示す完全なマップが得られることに注意してください。
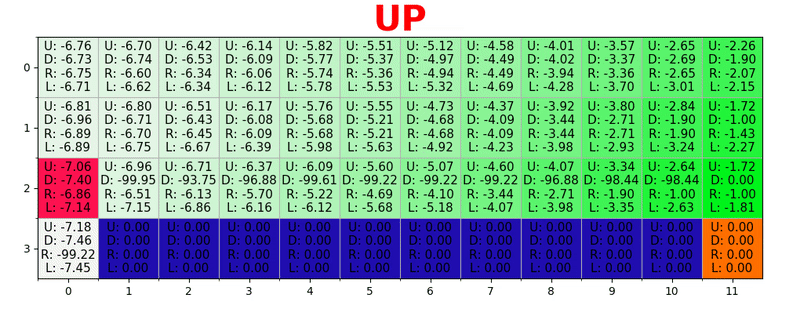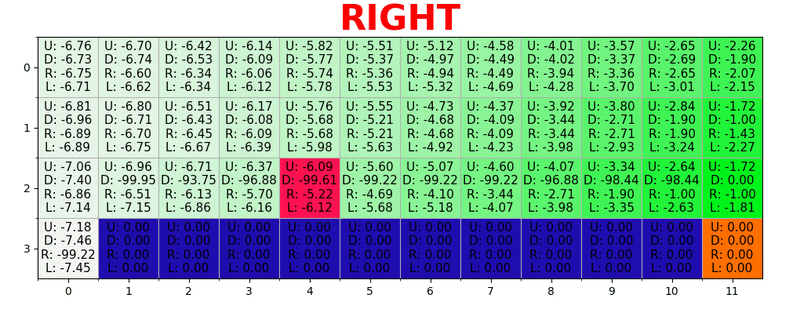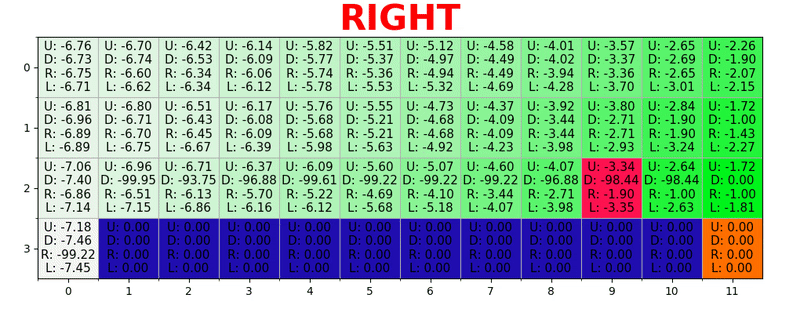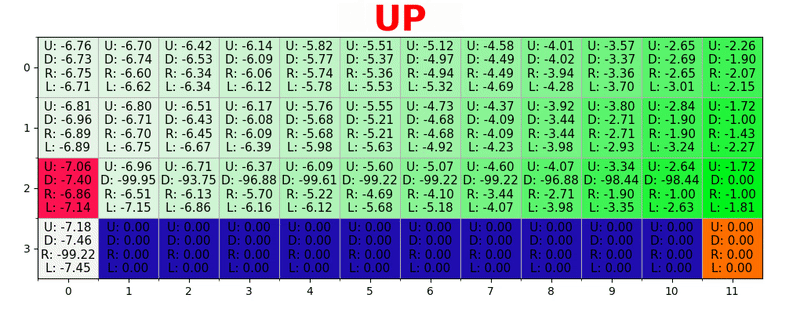
パスは、すべての状態で最適なアクションを実行することにより生成されます。 緑色のキーはより良いアクションの意味を表し、飽和したキーはより高い値を表します。 テキストは、各アクション(上、下、右、左)の値を表します。
ベルマン方程式
コードについて説明する前に、数学について説明しましょう。Qラーニングの基本概念であるベルマン方程式です。

- まず、この方程式のγを忘れましょう
- 方程式は、特定の状態とアクションのペアのQ値が、新しい状態への遷移時に(このアクションを実行することで)受け取った報酬であり、次の状態の最適なアクションの値に追加されることを示します。
つまり、アクション値を1ステップずつ配布します。
しかし、現時点で報酬を受け取ることは、将来報酬を受け取ることよりも価値があると判断できるため、0から1(通常は0.9から0.99)の数字であるγに将来の報酬を掛けて、将来の報酬を割引します。
したがって、γ= 0.9を与え、これを世界のいくつかの状態(グリッド)に適用すると、次のようになります。

これらの値を上記のGIFの値と比較して、同じであることがわかります。
実装
Qラーニングがどのように機能するかを直感的に理解できたので、このすべての実装について考え始めることができます。 サットンの本のQラーニング擬似コードをガイドとして使用します。

サットンの本からの擬似コード。
コード:
# Initialize Q arbitrarily, in this case a table full of zeros q_values = np.zeros((num_states, num_actions)) # Iterate over 500 episodes for _ in range(500): state = env.reset() done = False # While episode is not over while not done: # Choose action action = egreedy_policy(q_values, state, epsilon=0.1) # Do the action next_state, reward, done = env.step(action) # Update q_values td_target = reward + gamma * np.max(q_values[next_state]) td_error = td_target - q_values[state][action] q_values[state][action] += learning_rate * td_error # Update state state = next_state
- まず、「すべての状態とアクションについて、Q(s、a)を任意に初期化する」と言います。これは、好きな値でQ値のテーブルを作成できることを意味します。どんな種類のパーマネントであるかは問題ではありません。 2行目では、ゼロでいっぱいのテーブルを作成していることがわかります。
また、「最終状態のQの値はゼロです」と言います。最終状態ではアクションを実行できません。したがって、この状態のすべてのアクションの値はゼロと見なします。
- エピソードごとに、「Sを初期化する」必要があります。これは単に「ゲームを再開する」という派手な方法です。この場合、プレーヤーを開始位置に置くことを意味します。 私たちの世界には、まさにそれを行うメソッドがあり、6行目で呼び出しています。
- 各タイムステップ(行動する必要があるたび)で、Qから取得したアクションを選択する必要があります。
「すべての条件で最も価値のある行動を取っていますか?
これを行う場合、Q値を使用してポリシーを作成します。 この場合、私たちは常にあらゆる州で最高の行動を取るため、貪欲な方針になります。したがって、私たちは貪欲に行動すると言われています。
ジャンク
しかし、このアプローチには問題があります。1つは+1で、もう1つは+100の2つの報酬がある迷宮にいると想像してください(1つを見つけるたびにゲームは終了します)。 私たちは常に最高だと考える行動をとるので、最初に見つかった賞にとどまり、常にそれに戻ります。したがって、最初に+1賞を認めると、大きな+100賞を逃します。
解決策
世界を十分に研究したことを確認する必要があります(これは驚くほど難しい作業です)。 これがεの出番です。 貪欲なアルゴリズムのεは熱心に行動しなければならないことを意味しますが、時間の経過に伴うεの割合としてランダムなアクションを実行するには、無限の試行ですべての状態を調べる必要があります。
アクションは、イプシロン= 0.1の12行目のこの戦略に従って選択されます。これは、世界で10%の時間を研究していることを意味します。 ポリシーの実装は次のとおりです。
def egreedy_policy(q_values, state, epsilon=0.1): # Get a random number from a uniform distribution between 0 and 1, # if the number is lower than epsilon choose a random action if np.random.random() < epsilon: return np.random.choice(4) # Else choose the action with the highest value else: return np.argmax(q_values[state])
最初のリストの14行目で、stepメソッドを呼び出してアクションを完了します。世界は次の状態、報酬、ゲームの終了に関する情報を返します。
数学に戻る:
長い方程式があります。考えてみましょう。
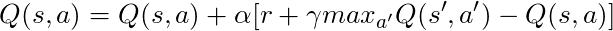
α= 1を取る場合:
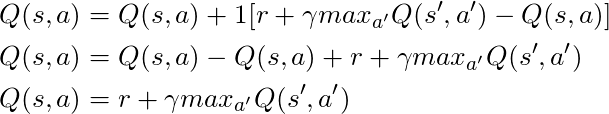
これは、数段落前に見たベルマン方程式と完全に一致します! したがって、これが状態値に関する情報を広める役割を果たしていることはすでにわかっています。
しかし、通常、α(ほとんどは学習速度として知られています)は1未満です。その主な目標は、1回の更新で大きな変更を避けることです。そのため、目標に飛び込むのではなく、ゆっくりとアプローチします。 表形式のアプローチでは、α= 1を設定しても問題は発生しませんが、ニューラルネットワークを使用する場合(これについては以下の記事で詳しく説明します)、すべてが簡単に手に負えなくなります。
コードを見ると、最初のリストの16行目でtd_targetを定義したことがわかりますが、これは近づくべき値ですが、17行目でこの値に直接移動する代わりに、td_errorを計算し、この値を速度と組み合わせて使用しますゆっくりと目標に向かって進むことを学ぶ。
この方程式はQラーニングエンティティであることを忘れないでください。
状態を更新するだけで、すべての準備が整いました。これは20行目です。エピソードの終わりに達するまで、岩で死ぬか、目標に達するまで、このプロセスを繰り返します。
おわりに
Q-Learning(少なくとも表形式のバージョン)をエンコードする方法を直感的に理解し、知っています。GitHubで利用できるこの投稿に使用されているすべてのコードを確認してください。
学習プロセステストの視覚化:
すべてのアクションは、その最終的な値を超える値で始まることに注意してください。これは、世界の探索を刺激するトリックです。