単純なルールと複雑な動作を備えたシステムの典型的な例は、セルオートマトンです。これは、ルールを見つけようとして焦点を当てたものです。 もちろん、セルオートマトンの場合、ほとんどの場合、ルールはより単純になります。 しかし、パーティクルはもっときれいにできます!
カットの下で、大量のgifが生成されます。
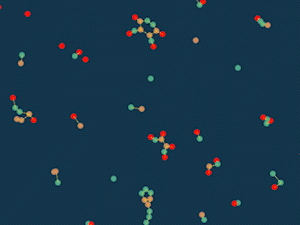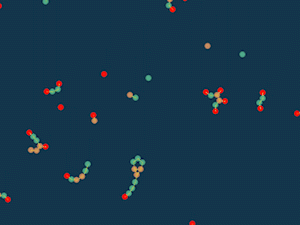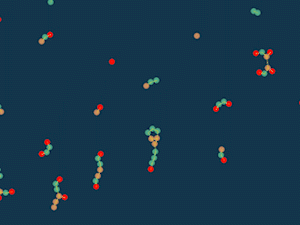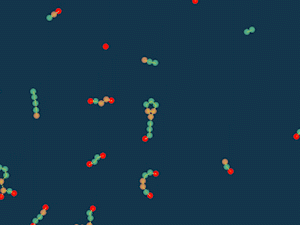
セルスープ
まず、「ライフ」ゲームの足跡をたどりました。各パーティクルには「人口過多」カウンターがあり、これは他のパーティクルまでの距離の逆二乗の合計に等しくなります。 このカウンターが特定の制限よりも小さい場合、つまり、近隣が少ない場合、パーティクルは他のパーティクルに引き付けられ、近隣が多い場合は反発されます。 粒子が交差する場合、互いに通過しないように、いずれの場合も反発します。
フィールドの周囲にランダムに粒子を散布し、何が起こるかを確認します。

興味深いことに、それは細胞に似たものであり、すでにかなり活発に見えます。 たとえば、さらに多くの種類のパーティクルを追加できます。 異なる粒子が異なる方法で隣人の数を増やすようにし、いくつかはそれを減らすことさえできます。

今、私たちの「細胞」は多層になっています。
このようなルールの欠点は、非常に安定した構造ではなく、かなり混oticとした構造を生成することです。
したがって、次に進みます。
追いつきゲーム
ゲームのルールを変更します。 隣人はもう数えません。 粒子は、そのタイプに応じて単純に引き付けたり反発したりします。 すべてのパーティクルが同じタイプである場合、2つのオプションしかありません。それらはすべて反発するか、すべて引き付けます。

より多くの種類の粒子がある場合、ここでどの粒子が引き寄せられ、どの粒子から反発されるかを組み合わせることができます。
非表示のテキスト
引力/反発に加えて、たとえば、粒子が互いに反応しないように他のオプションを追加したり、影響力に係数を追加したりすることもできますが、これには興味深い動作が見つかりませんでした。
このような規則は、マトリックスN * Nの形式で表すことができます。ここで、Nは粒子の種類の数であり、各セルには引力または反発力があります。 引力は0で示され、反発力は1で示されます。その後、任意のマトリックスは特定の数に対応します。たとえば、マトリックス は、0101、つまり5を意味します(バイナリ形式の最後の数字は、マトリックスの最初の数字です)。 ルールの異なる行列の数は 。 たとえば、2種類のパーティクルの場合、16のルールがあります。

ルール3はルール7と同じように見えるかもしれませんが、それらを行列に変換すると、 そして 、これは、ルール7ではベージュだけが互いに引き付けられることを意味します。 ルール3では、ベージュも赤に惹かれます。 しかし、赤の密度が低いため、微妙な効果があります。 実際、たとえば3と12のように、同じ規則を呼び出すことができます。これは、パーティクルの動作全体が同じであるため、色のみが場所を変更したためです。 一意の動作を持つルールのみを残す場合、16個のルールのうち10個になります。512の可能な組み合わせのうち3つのタイプのパーティクルには104個の一意のものが残り、4つには65536から3044のシーケンスが得られます。
しかし、10のルールに戻ります。

マトリックスであるルール9は目を引く 、同じ反発、および異なる引き付けます。 ランダムに散らばった粒子はすぐに「糸」を形成し、これでフリーズします。
ルール1と15もフリーズします。これらは、1種類のパーティクル(以前のアニメーションGIF)の2つの単一ルールと同等です。 通常、すべてのルールが設定され、そのマトリックスは対称です。 非対称マトリックスにはまだルール2、3、5、および11があります。 つまり、1種類の粒子が2番目の粒子に引き付けられ、2番目の粒子が最初の粒子からはじかれます。 追いつきが始まります。

ルール3は安定しすぎており、ある時点で「追いつき」が止まり、再開した場合、めったになく、長くは続かない。 ルール11は無秩序です。 2と5のままです。
それらを何らかの形で組み合わせて、さらに面白くすることができます。 私は3つの色、つまりマトリックスのルール105を選びました 、これは動作です:

それはすべて活発に見えますが、不安定です。 しかし、特定の繰り返される「生きている」クリーチャーはどうでしょうか? オシレーターとグライダーの検索方法は? ルールを再度変更する必要があります!
フローティングライフ
ルールはあまり変更しません。 代わりに、新しい機能を追加してください。 これで、粒子は短い距離で結合を形成します。 パーティクルがバインドされている場合、それらは常に互いに引き付けられます。 この魅力は距離とともに弱まることはありません。 ただし、距離が特定のしきい値を超える場合、接続は切断されます。
私は3つの色で異なるオプションを試し、赤が1つの接続のみを形成できる場所に落ち着きました、ベージュ-3、青-2、つまり、フォームで最大の接続を指定できます 。
同時に、赤は他の赤と結合できず、ベージュと青は、それぞれの色の粒子と2つ以下の結合しか持たず、互いの色の粒子とは1つしか結合できません。 これはすべてマトリックス形式です。

さまざまなプル/プッシュルールを試し、気に入った 、つまり、赤いものは青いものに引き付けられ、他のすべての場合はすべて反発されます。

これらの生き物は液体に浮かんでいるか、羽ばたきしているようです。


オシレーターのペアとグライダーのペア。
固定図は簡単に入手できます。赤と青を一緒に使用する必要はありません。これらのルールでは、これが魅力との唯一の組み合わせです。


しかし、時々、そのような色で動きが起こります。 いくつかの図が回転し始め、他の図から始まり、「ギア」が得られます。

おわりに
将来、得られた数字を比較して、出現頻度に関する統計を収集することは興味深いでしょう。
これらのルールは、食物、生殖、進化を伴うより複雑な生き物を作成するための基礎として使用することもできます。
プレイする
v1vendiからのJS実装
ソースコード
Javaコード
同様のクールなもの
コスモス
粒子寿命
クラスター