フィリップギブスは、困難な幾何学的計算を通じて、あらゆる形状の最小の既知のコーティングを発見しました。
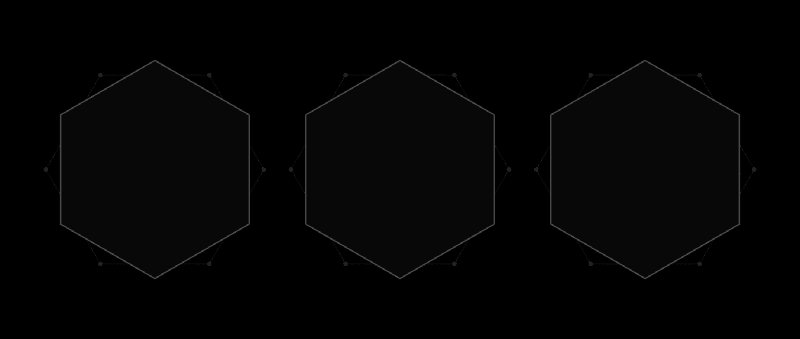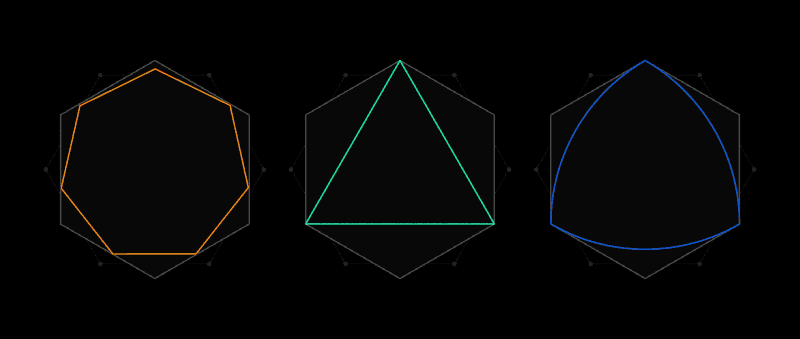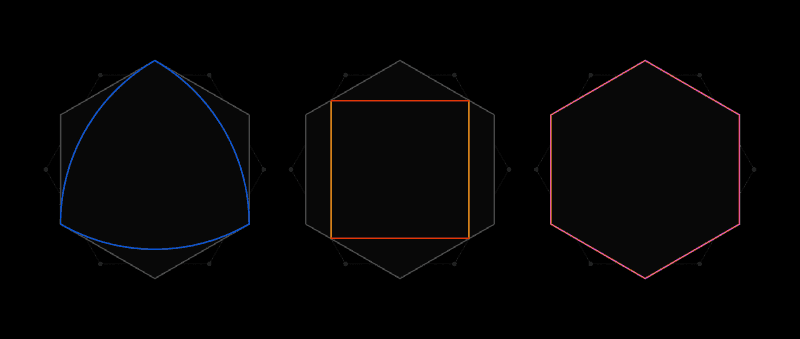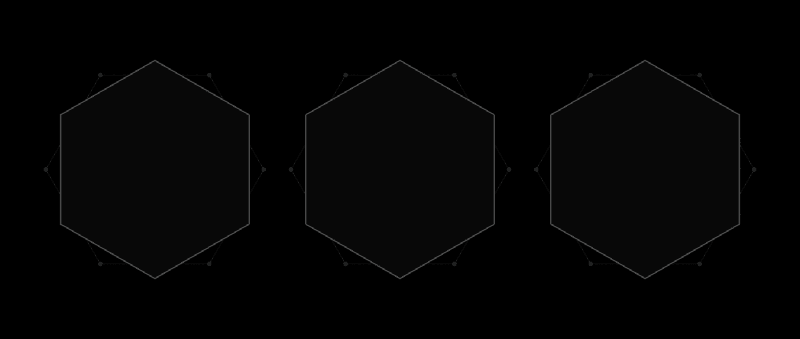
六角形などの普遍的なカバーは、あらゆる形状の周りに記述できます。
フィリップギブスはプロの数学者ではありません。 したがって、彼が仕事を振り返りたいと思ったとき、彼はアマチュアが処理できるものを探していました。 彼は、最高の頭脳をも狂わせることができる難しい仕事を発見しました。 今年発行された論文で、ギブスは、原子スケールまでの面積を正確に測定する能力に応じて、100年前の問題の解決に大きな進歩を遂げました。
この仕事を最初に提案したのは、1914年に書かれた友人のジュリアスパルへの手紙で、フランスの数学者アンリレオンルベーグでした。 ルベーグは尋ねました:多数の他のフォームを完全にカバーできる、可能な限り小さい領域の形状は何ですか(以下に説明する1つの共通のプロパティを持っています)?
過去1世紀にわたって、普遍的なカバーを見つける作業はネズミ捕りに変わりました。それが定期的に発生した場合、それを解決する進歩は常に驚くほど小さいものでした。 これに対するギブスの改善は劇的になりました-まだ少し考える必要がありますが。
床に横たわっているさまざまなサイズや形の切り抜きがたくさんあると想像してください。 ここで、既存の形状をすべてカバーするのに十分な大きさの別の形状を考え出すように提案されていると想像してください。 実験を通して-フォームを重ね合わせて反転させることにより、この問題を解決する方法を思いつくことができます。 しかし、普遍的なカバレッジを見つけたので、最小のものを見つけたと確信できますか? 日中は定期的にフォームに戻り、あちこちで追加のピースを切り取る機会を見つけることが想像できます。
これが、ルベーグの普遍的なカバレッジ問題の精神です。 紙の切り抜きの代わりに、任意の2つのポイントが1単位の長さを超えない間隔で配置されているフォームを考慮します。 最も明白な形状は直径1の円ですが、無限の数があります:正三角形、正五角形、正六角形、ふくらんでいる側面を備えた三角形、Röhlo三角形 -これは単なるスターター用です。 多様な形式により、それらすべての最小のカバレッジを見つけることは困難です。
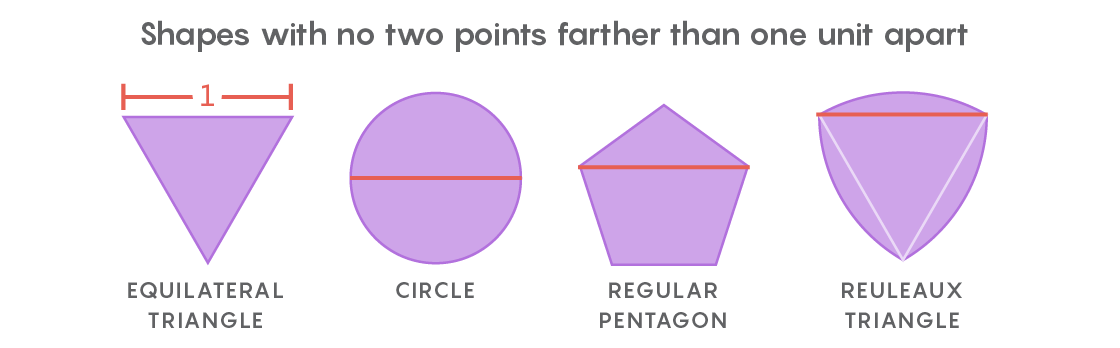
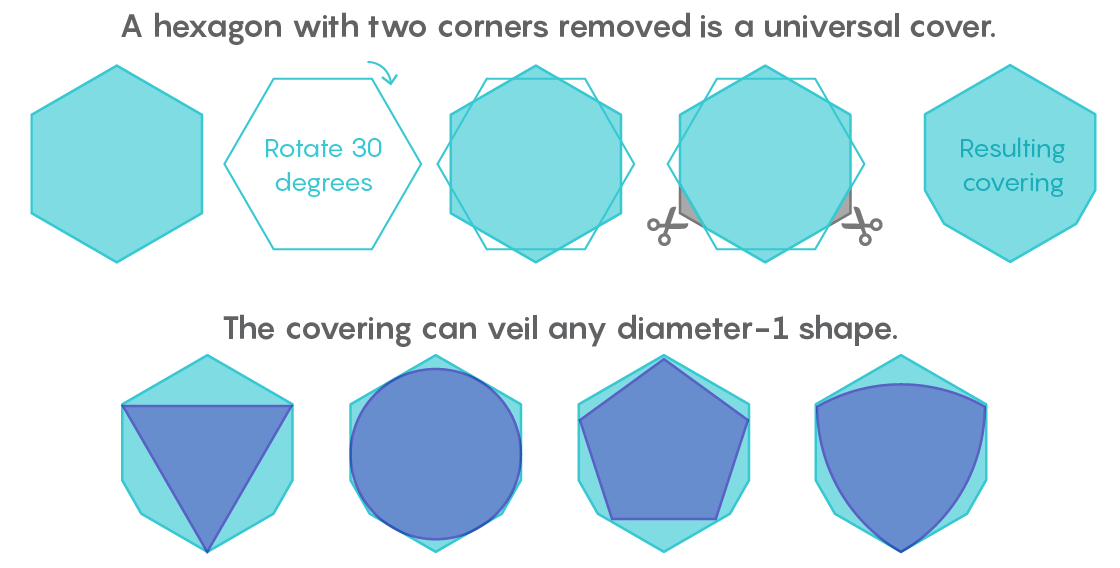
Lebesgueからの手紙を受け取って間もなく、Palは正六角形が普遍的なカバーになることに気付きました。 そして、彼はこの結果を改善しました。六角形の2つの角を互いに隣接せずに切断することで、より小さな面積の形状を得ることができ、これはまだ普遍的なコーティングであることがわかります。
「六角形を取り、その上に2つ目の六角形を置き、30度回転して、2つの角を切り取ります。 そこでパルは研究を終了しました」とギブスは言いました。
次の80年で、他の2人の数学者がパルの普遍的なカバーから狭いストリップを切り取りました。 1936年、ローランド・スプラグは角の一つの隣にある小片を取り除いた。 1992年、ハンセンは右下と左下の角から2つの小型のくさびを取り除きます。 ハンセンのイラストは、これらの部品の位置を伝えることはできましたが、サイズではありませんでした。面積は0.00000000004単位でした。
カリフォルニア大学リバーサイド校の数学者ジョン・バエズは、「スケールで描くことはできません。原子の大きさになるでしょう」と述べました。
Baezは2013年に人気のある数学についてブログで書いたときに、レベグエの仕事を忘却から取り除いた。 彼は、task死する昆虫のビデオがあなたを魅了できるように、このタスクに魅了されたことを認めました。 「タスクに対する私の関心は不健康でした」とBAezは書いた。 「それが重要である理由はわかりません。」 他の多くの素晴らしいタスクとどのように結びつくかわかりません。 第一印象と比べると、信じられないほど複雑に思えます。 私は、スキーで南極大陸を横断することを決めた人々を賞賛するのと同じくらい、それに取り組んでいる人々を賞賛します。」
フィリップギブスはスキーで南極大陸を横断したことはありませんが、バエズのブログを読んでください。 彼はルベーグの問題の記録に会ったとき、「まあ、まさにそれが私に必要なものだ」と考えました。
アトミックハサミ
ギブスはかつて自分が科学者になることができると考えていました。 彼はケンブリッジ大学で数学の学位を、グラスゴー大学で理論物理学の博士号を取得しました。 しかし、彼はすぐに学術研究への熱意を失い、プログラマーになりました。 彼は、船舶設計、航空交通管理、財務のシステムに取り組み、2006年に退職しました。
ギブスは引き続き学問に興味がありましたが、一般の研究者としてはほとんど何もできませんでした。 「独立した科学者が何が起こっているかを追跡するのは難しいです」と彼は言いました。 「しかし、適切なニッチを見つけることができれば、何かをして有益な結果を得ることができます。」

アマチュア数学者フィリップ・ギブス
そのようなニッチは、ルベーグの普遍的なカバレッジの問題でした。 このタスクは数学者の注目を決して受けなかったため、彼はある程度の進歩を達成できると疑っていました。 ギブスはまた、彼のプログラミング経験が利点になる可能性があることに気づきました。 「コンピューターと実験数学を使用できる問題を常に探しています」と彼は言いました。
2014年、Gibbsは直径1の200のランダムなフォームに対してコンピューターシミュレーションを実行しました。シミュレーションから、彼は以前の最小のカバーの上部コーナーから小さなピースをカットできる可能性があることになりました。 彼はこれを直径1のすべての可能な形状に対して機能するという証明に変えました。ギブスはその証明をバエズに送りました。
3人は2015年2月に彼らの作品をインターネットで公開しました。これにより、最小のユニバーサルカバレッジの領域が0.8441377から0.8441153ユニットに縮小されました。 0.0000224単位の節約は、ハンセンが1992年に達成したもののほぼ100万倍でした。
ギブスは、結果を改善できると確信していました。 10月に公開された作品で、彼はユニバーサルコーティングから別の比較的大きな塊を切り取り、その面積を0.84409359単位にしました。
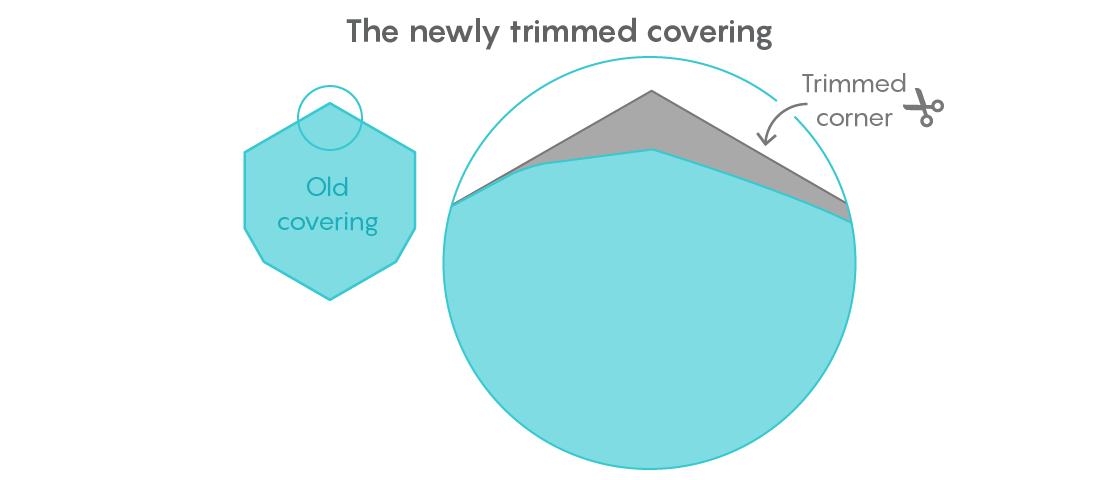
彼の戦略は、直径1のすべてのフォームを数年前に発見したユニバーサルコーティングの角に移動し、反対側の角の残りの領域全体を削除することでした。 しかし、節約されたスペースを正確に測定することは困難です。 ギブスが使用する技術はユークリッド幾何学に基づいていましたが、高校生に衝撃を与えるほど正確に実行されました。
「数学の観点から見ると、これはすべて高校の幾何学です。 しかし、熱狂的な緊張で行われた」とバエズは書いた 。
これまでのところ、ギブスは最小の普遍的なカバレッジの検索で1位を保持していますが、彼の賞は危険にさらされています。 Gibbsは、カバレッジをさらに小さくする機会があると考えています。 バエズは、ギブスがルベーグ問題に戻ったという注意が他の数学者の関心を刺激することを望んでいます。 おそらく、定規とコンパスを脇に置き、現代数学の兵器庫全体を使用する時が来たのでしょう。
「この謎を解く正しい方法は、まったく異なるアイデアを使用する可能性があります」と彼は言いました。