動的システムのジュリアと位相の肖像

私たちは、若くて有望な汎用言語ジュリアを習得し続けます。 しかし、まず最初に、典型的な物理学の問題を解決するために、非常に狭い適用の可能性が必要です。 これは、楽器を習得するための最も便利な戦術です。手を伸ばすために、差し迫った問題を解決し、徐々に複雑さを増し、人生を楽にする方法を見つけます。 要するに、ディファーを解決してグラフを作成します。

始めるには、 Gadflyグラフィックパッケージをダウンロードし、すぐに開発者のフルバージョンをダウンロードして、Julia 1.0.1で正常に動作するようにします。 REPL、JUNO、またはJupyterノートブックでドライブします。

using Pkg pkg"add Compose#master" pkg"add Gadfly#master"
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

最も便利なオプションではありませんが、 PlotlyJSの更新を待っている間に、比較のために試すことができます 。

また、微分方程式を解くための強力なツールも必要です。

 ]add DifferentialEquations #    
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これは最も広範でサポートされているパッケージで、さまざまな問題を解決するための多くの方法を提供します。 次に、フェーズのポートレートに進みます。

常微分方程式の解法は、通常は、通常とは異なる形式で表現する方が便利です。 $$$y ^ 1（t）、...、y ^ L（t）$ 、および見つかった各関数の値がプロットされる軸に沿った位相空間で 。 さらに、引数tは、パラメトリックにのみグラフに含まれます。 2つのODEの場合、このようなグラフ（システムの位相の肖像）は位相平面上の曲線であるため、特に顕著です。

発振器

調和振動子ダイナミクス $$$\ガンマ$ 次の連立方程式によって記述されます。

$$

$$\ dot {x} = y \\ \ dot {y} =-\ omega ^ 2x + \ gamma y$$

そして、初期条件（x0、y0）に関係なく、平衡状態、つまり偏向角と速度がゼロの点（0,0）になります。

で $$$\ガンマ= 0$ 解決策は、古典的な発振器に特有の形式を取ります。

 using DifferentialEquations, Gadfly #     -    function garmosc(ω = pi, γ = 0, x0 = 0.1, y0 = 0.1) A = [0 1 -ω^2 γ] syst(u,p,t) = A * u # ODE system u0 = [x0, y0] # start cond-ns tspan = (0.0, 4pi) # time period prob = ODEProblem(syst, u0, tspan) # problem to solve sol = solve(prob, RK4(),reltol=1e-6, timeseries_steps = 4) N = length(sol.u) J = length(sol.u[1]) U = zeros(N, J) for i in 1:N, j in 1:J U[i,j] = sol.u[i][j] #      end U end
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

コードを分析しましょう。 この関数は、周波数と減衰パラメーターの値、および初期条件を受け入れます。 ネストされたsyst（）関数はシステムを定義します。 1行にするために、行列乗算を使用しました。 膨大な数のパラメーターをとるsolve（）関数は、問題を解決するために非常に柔軟に構成されていますが、ソリューションメソッド-Runge-Kutta 4（ 他にも多くあります ）、相対誤差、およびすべてのポイントを保存する必要はありませんが、 。 応答行列は変数solに格納され、さらにsol.tには時間の値のベクトルが含まれ、これらの時間におけるシステムの解のsol.uが含まれます。 これはすべてPlotsで落ち着いて描かれています。Gadflyの場合は、より便利なマトリックスで答えを記入する必要があります 。 時間は必要ないので、ソリューションのみを返します。

フェーズポートレートを作成しましょう。

 Ans0 = garmosc() plot(x = Ans0[:,1], y = Ans0[:,2])
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

高次関数の中で、 broadcast(f, [1, 2, 3])



は特に顕著であり、配列[1、2、3]の値を関数fに交互に置き換えます。 短いレコードf.([1, 2, 3])



。 これは、周波数、減衰パラメータ、初期座標、および初期速度を変えるのに役立ちます。

ここで、小さな振動ではなく、任意の振幅の振動を考慮します。

$$

$$\ dot {x} = y \\ \ dot {y} =-sin（\ omega x）+ \ gamma y$$

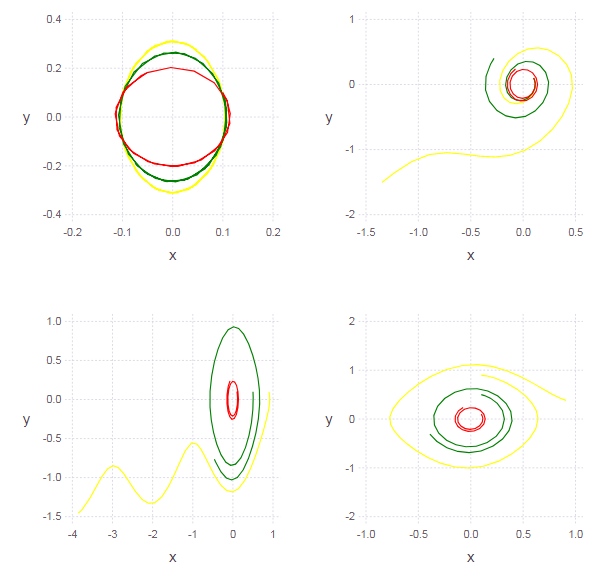
位相平面上の解のグラフは楕円ではありません（これは振動子の非線形性を示します）。 振動の振幅（つまり、初期条件）を選択するほど、非線形性が少なくなります（したがって、振り子の小さな振動は高調波と見なすことができます）。

ブリュッセル

このモデルは、拡散が役割を果たす特定の自己触媒化学反応を記述します。 このモデルは、1968年にLefebvreとPrigozhinによって提案されました。

$$

$$\ dot {u} _1 =-（\ mu + 1）u_1 + u ^ 2_1u_2 + 1 \\ \ dot {u} _2 = \ mu u_1-u ^ 2_1u_2$$

不明な機能 $$$u_1（t）、\、u_2（t）$ 化学反応の中間生成物の濃度のダイナミクスを反映します。 モデルパラメータ $$$\ mu$ 触媒（3番目の物質）の初期濃度は理にかなっています。

より詳細には、さまざまなパラメータを使用して計算を実行することで、ブルセレーターの位相ポートレートの進化を観察できます。 $$$\ mu$ 。 ノードが増加すると、ノードはまず座標（1、 $$$\ mu$ ） 分岐値に達するまで $$$\ mu$ = 2。 この時点で、究極のサイクルの誕生で表現された肖像画の質的な再構築があります。 さらに増加し​​て $$$\ mu$ このサイクルのパラメーターの定量的変化のみが発生します。

今日はこれで十分です。 次回は、新しいタスクに別のグラフィックパッケージを使用する方法を学習すると同時に、ジュリアの構文に手を入力します。 問題を解決する過程で、長所と短所が単純であるということではなく、ゆっくりと追跡され始めています...むしろ、快適さと不便-これに別の会話を捧げるべきです。 そしてもちろん、機能を備えたゲームよりもHaberでもっと深刻なものを見たいと思っています。したがって、ジュリストにもっと深刻なプロジェクトについてもっと教えてくれるよう強くお勧めします。これは多くの、特にこの素晴らしい言語を学ぶのに役立ちます。