無効な状態をさらに話すことができないようにする方法

少し前まで、 Habrで代数データ型を使用して誤った状態を表現できないようにする方法に関する記事が翻訳されました。 今日は、表現しにくい表現を表現するために、少し一般化された、スケーラブルで安全な方法を検討しますが、Haskellはこれを支援します。

要するに、その記事では、メールアドレスとメールアドレス、およびこれらのアドレスの少なくとも1つが存在する必要があるという追加の条件を持つエンティティについて説明しています。 この条件を型レベルでどのように表現することが提案されていますか？ 次のようにアドレスを記述することが提案されています。

type ContactInfo = | EmailOnly of EmailContactInfo | PostOnly of PostalContactInfo | EmailAndPost of EmailContactInfo * PostalContactInfo
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

このアプローチにはどのような問題がありますか？

最も明白な（そしてその記事へのコメントで何度か指摘されている）ことは、このアプローチはまったくスケーラブルではないということです。 2種類のアドレスではなく、3種類または5種類のアドレスがあり、「メールアドレス、またはメールアドレスとオフィスアドレスの両方が必要であり、同じタイプのアドレスが複数あってはならない」という正確性条件があります。 希望する人は、セルフテストの練習として適切なタイプを書くことができます。 アスタリスクが付いているタスクは、重複がないことに関する条件がTORから消えた場合に、このタイプを書き換えることです。

共有する

この問題を解決するには？ 想像してみてください。 まず、アドレスクラス（たとえば、オフィスのメール/メール/デスク番号）とこのクラスに対応するコンテンツを分解して分離します。

 data AddrType = Post | Email | Office
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

TKにはアドレスリストの有効性に関する条件がないため、コンテンツについてはまだ検討しません。

通常のOOP言語のコンストラクターのランタイムで対応する条件をチェックした場合、次のような関数を書くだけです。

 valid :: [AddrType] -> Bool valid xs = let hasNoDups = nub xs == xs --      hasPost = Post `elem` xs hasEmail = Email `elem` xs hasOffice = Office `elem` xs in hasNoDups && (hasPost || (hasEmail && hasOffice))
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

False



返した場合、何らかの実行をスローします。

代わりに、コンパイル時にタイマーを使用して同様の条件をチェックできますか？ その言語の型システムが十分に表現力豊かであれば、はい、できます。記事の残りの部分では、このアプローチを選択します。

ここでは依存型が非常に役立ちます。Haskellで検証済みコードを記述する最も適切な方法は、AgdeまたはIdrisで最初に記述することなので、靴を変えてIdrisで記述します。 idris構文はHaskellにかなり近いです。たとえば、前述の関数を使用すると、署名をわずかに変更するだけで済みます。

 valid : List AddrType -> Bool
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ここで、アドレスクラスに加えて、コンテンツも必要であり、アドレスクラスのフィールドの依存関係をGADTとしてエンコードすることを思い出してください。

 data AddrFields : AddrType -> Type where PostFields : (city : String) -> (street : String) -> AddrFields Post EmailFields : (email : String) -> AddrFields Email OfficeFields : (floor : Int) -> (desk : Nat) -> AddrFields Office
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

つまり、 AddrFields t



型のfields



値が与えられた場合、 t



はクラスAddrType



であり、 fields



AddrType



この特定のクラスに対応するフィールドのセットがAddrType



ことがAddrType



ます。

 addrFields : AddrType -> Type addrFields Post = PostFields addrFields Email = EmailFields addrFields Office = OfficeFields
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

このモデルの住所全体は何ですか？ これは、アドレスクラスと対応するフィールドのペアです。

 Addr : Type Addr = (t : AddrType ** AddrFields t)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

型理論の愛好家は、これが存在依存型であると言うでしょう：もしAddr



型の値が与えられたら、これはAddrType



型の値t



と対応するフィールドAddrFields t



セットがあることをAddrFields t



ます。 当然、異なるクラスのアドレスには同じタイプがあります。

 someEmailAddr : Addr someEmailAddr = (Email ** EmailFields "that@feel.bro") someOfficeAddr : Addr someOfficeAddr = (Office ** OfficeFields (-2) 762)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

さらに、 EmailFields



が与えられた場合、適切なアドレスクラスはEmail



であるため、省略することができ、タイマーは自分でそれを表示します。

 someEmailAddr : Addr someEmailAddr = (_ ** EmailFields "that@feel.bro") someOfficeAddr : Addr someOfficeAddr = (_ ** OfficeFields (-2) 762)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

アドレスリストから対応するアドレスクラスのリストを提供する補助関数を作成し、すぐにそれを任意のファンクターで動作するように一般化します。

 types : Functor f => f Addr -> f AddrType types = map fst
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ここで、実在するAddr



タイプはおなじみのカップルのように動作します。特に、最初のコンポーネントAddrType



を要求できます（アスタリスク付きのタスク：なぜ2番目のコンポーネントを要求できないのですか？）。

上げる

次に、ストーリーの重要な部分に進みます。 したがって、 List Addr



アドレスのリストといくつかのvalid : List AddrType -> Bool



述語がありvalid : List AddrType -> Bool



、このリストの実行は型のレベルで保証したいです。 それらをどのように組み合わせるのですか？ もちろん、別のタイプです！

 data ValidatedAddrList : List Addr -> Type where MkValidatedAddrList : (lst : List Addr) -> (prf : valid (types lst) = True) -> ValidatedAddrList lst
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

次に、ここで書いたことを分析します。

data ValidatedAddrList : List Addr -> Type where



で、タイプValidatedAddrList



、実際にはアドレスリストによってパラメーター化されます。

このタイプの唯一のMkValidatedAddrList



コンストラクターのシグネチャを見てみましょう： (lst : List Addr) -> (prf : valid (types lst) = True) -> ValidatedAddrList lst



MkValidatedAddrList



(lst : List Addr) -> (prf : valid (types lst) = True) -> ValidatedAddrList lst



。 つまり、 lst



アドレスのリストと、 valid (types lst) = True



別のprf



引数を取りvalid (types lst) = True



。 このタイプはどういう意味ですか？ これは、 =



の左側の値が=



の右側の値に等しいことを意味します。つまり、 valid (types lst)



、実際にはTrueです。

どのように機能しますか？ 署名=



(x : A) -> (y : B) -> Type



ます。 つまり、 =



は2つの任意の値x



とy



取ります（異なる型A



とB



場合もあります。これは、idrisの不等式が不均一であり、型理論の観点からは多少曖昧であることを意味しますが、これは別の議論のトピックです）。 何が平等を実証しますか？ そして、唯一のコンストラクタ=



Refl



がほとんど (x : A) -> x = x



シグネチャを持つという事実のため。 つまり、タイプx = y



値がある場合、（他のコンストラクターがないため） Refl



を使用して構築されたことがわかります。つまり、 x



は実際にはy



と等しいことを意味します。

Haskellでは、あらゆるタイプに生息するundefined



あるため、Haskellでは常に最高のふりをするので、上記の引数はそこで機能しないことに注意してください： x



、 y



タイプx = y



はundefined



（または無限再帰、一般的には型理論の観点からは同じである）によって作成できます。

ここでの平等は、HaskellのEq



やC ++のoperator==



の意味ではなく、かなり厳密なものであることに注意してください。構造、つまり、2つの値が同じ形式であることを意味します。 つまり、彼をだまそうとするだけではうまくいきません。 しかし、平等の問題は伝統的に別の記事に描かれています。

平等の理解を統合するために、 valid



関数の単体テストを作成します。

 testPostValid : valid [Post] = True testPostValid = Refl testEmptyInvalid : valid [] = False testEmptyInvalid = Refl testDupsInvalid : valid [Post, Post] = False testDupsInvalid = Refl testPostEmailValid : valid [Post, Email] = True testPostEmailValid = Refl
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

これらのテストは、実行する必要さえないという点で優れています。テプチャーがチェックするだけで十分です。 実際、たとえば最初のTrue



をFalse



に置き換えて、何が起こるか見てみましょう。

 testPostValid : valid [Post] = False testPostValid = Refl
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

Typsekherは誓う

予想通り。 いいね

簡素化

次に、 ValidatedAddrList



少しリファクタリングしましょう。

まず、特定の値とTrue



を比較するパターンTrue



非常に一般的です。したがって、このidrisには特別なタイプSo



があります。Soxをx = True



同義語として取ることができx = True



。 ValidatedAddrList



の定義を修正しましょう。

 data ValidatedAddrList : List Addr -> Type where MkValidatedAddrList : (lst : List Addr) -> (prf : So (valid $ types lst)) -> ValidatedAddrList lst
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

さらに、 So



には便利な補助関数choose



があり、本質的にチェックを型のレベルに引き上げます。

 > :doc choose Data.So.choose : (b : Bool) -> Either (So b) (So (not b)) Perform a case analysis on a Boolean, providing clients with a So proof
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

このタイプを変更する関数を作成するときに役立ちます。

第二に、時々（特にインタラクティブな開発の場合）、idrisは適切なprf



値prf



独自に見つけることができます。 そのような場合に手作業で構築する必要がなかったために、対応する構文糖があります：

 data ValidatedAddrList : List Addr -> Type where MkValidatedAddrList : (lst : List Addr) -> {auto prf : So (valid $ types lst)} -> ValidatedAddrList lst
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

中括弧は、これがidrisがコンテキストから抜け出そうとする暗黙の引数であることを意味し、 auto



は彼が自分でそれを構築しようとすることを意味します。

では、この新しいValidatedAddrList



は何を提供しますか？ そして、それはそのような推論の連鎖を与えます： val



ValidatedAddrList lst



型の値にします。 つまり、 MkValidatedAddrList



はアドレスのリストであり、さらにval



はMkValidatedAddrList



コンストラクターを使用して作成されました。このMkValidatedAddrList



ターには、このMkValidatedAddrList



、 So (valid $ types lst)



prf



値を渡しました。 valid (types lst) = True



。 そして、 prf



を構築できるように、実際には、この平等が成り立つことを証明する必要があります。

そして最も美しいのは、これがすべて暗号によってチェックされることです。 はい、有効性のチェックはランタイムで行う必要があります（アドレスはファイルまたはネットワークから読み取ることができるため）が、タイマーはこのチェックが行われることを保証します：それなしではValidatedAddrList



を作成することはできません。 少なくともidrisでは。 Haskell、悲しいかな。

挿入

検証の必然性を検証するために、リストにアドレスを追加する関数を記述しようとします。 最初の試行：

 insert : (addr : Addr) -> ValidatedAddrList lst -> ValidatedAddrList (addr :: lst) insert addr (MkValidatedAddrList lst) = MkValidatedAddrList (addr :: lst)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

いいえ、タイポチェッカーは指に与えます（非常に読みやすくはありませんが、 valid



のコストは複雑すぎます）。

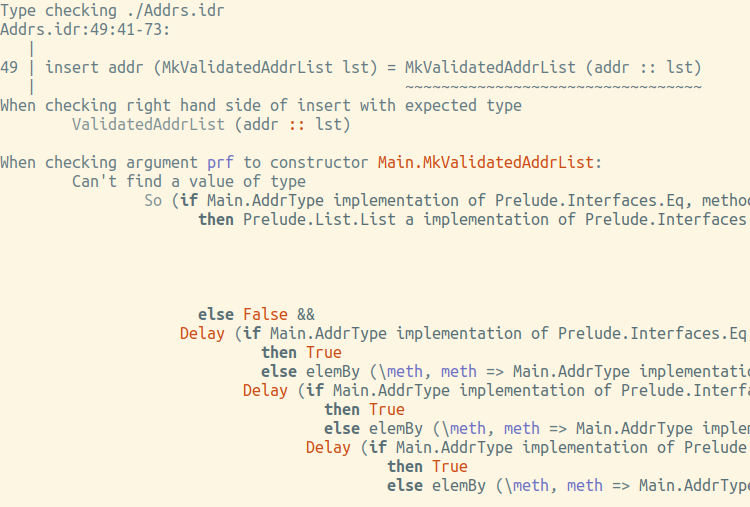
どうやってこれのコピーを手に入れるの？ それ以外の場合は、前述のchoose



よりも。 2回目の試行：

 insert : (addr : Addr) -> ValidatedAddrList lst -> ValidatedAddrList (addr :: lst) insert addr (MkValidatedAddrList lst) = case choose (valid $ types (addr :: lst)) of Left l => MkValidatedAddrList (addr :: lst) Right r => ?rhs
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

それはほとんどtypecheketsyaです。 rhs



代わりに何を使用するかが明確でないため、「ほぼ」。 むしろ、明らかです。この場合、関数は何らかの形でエラーを報告する必要があります。 そのため、たとえば、 Maybe



、署名を変更して戻り値をラップする必要があります。

 insert : (addr : Addr) -> ValidatedAddrList lst -> Maybe (ValidatedAddrList (addr :: lst)) insert addr (MkValidatedAddrList lst) = case choose (valid $ types (addr :: lst)) of Left l => Just $ MkValidatedAddrList (addr :: lst) Right r => Nothing
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

それはtycheketsyaとそれがするべきように動作します。

しかし、今ではそれほど明白ではない次の問題が発生します。これは実際には元の記事にありました。 この関数のタイプは、そのような実装の作成を停止しません。

 insert : (addr : Addr) -> ValidatedAddrList lst -> Maybe (ValidatedAddrList (addr :: lst)) insert addr (MkValidatedAddrList lst) = Nothing
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

つまり、アドレスの新しいリストを作成できなかったと常に言います。 Typhechaetsya？ はい 正しいですか？ まあ、ほとんど。 これは回避できますか？

それが可能であることが判明し、これに必要なすべてのツールがあります。 成功した場合、 insert



はValidatedAddrList



返します。これには、この成功の証拠が含まれています。 エレガントな対称性を追加し、失敗の証拠も返すように関数に依頼してください！

 insert : (addr : Addr) -> ValidatedAddrList lst -> Either (So (not $ valid $ types (addr :: lst))) (ValidatedAddrList (addr :: lst)) insert addr (MkValidatedAddrList lst) = case choose (valid $ types (addr :: lst)) of Left l => Right $ MkValidatedAddrList (addr :: lst) Right r => Left r
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

今では、単にNothing



取得して常に返すことはできませNothing



。

同じことは、アドレス削除機能などについても行うことができます。

それがすべてどのように見えるかを見てみましょう。

空のアドレスリストを作成してみましょう。

不可能です。空のリストは無効です。

郵送先住所のリストはどうですか？

さて、すでに住所を持っているリストに住所を挿入してみましょう：

メールを挿入してみましょう：

最終的に、すべてが期待どおりに機能します。

ふう。 3行になると思いましたが、少し長くなりました。 それで、Haskellをどこまで進めることができるかを探るには、次の記事に行きます。 それまでの間、少し

熟考

最後に、そのような決定の利益は、最初に言及した記事で与えられたものと比較して何ですか？

1. これもまた、はるかにスケーラブルです。 複雑な検証関数は簡単に記述できます。
2. より分離されています。 クライアントコードでは、検証関数の内容を知る必要はありませんが、元の記事のContactInfo
   
   
   
   フォームでは、結び付ける必要があります。
3. 検証ロジックは通常の使い慣れた関数の形式で記述されているため、すでに検証済みの結果を表すデータ型フォームから検証の意味を導出するのではなく、思慮深い読み取りですぐにチェックし、コンパイル時テストでテストできます。
4. 特にテストに合格しなかった場合に、対象のデータ型で機能する関数の動作をより正確に指定することが可能になります。 たとえば、結果として書き込まれたinsert
   
   
   
   は、 誤って書き込むことは不可能です。 同様に、 insertOrReplace
   
   
   
   、 insertOrIgnore
   
   
   
   などを記述することもできますが、その動作は型で完全に指定されます。

そのようなOOPソリューションと比較した場合の利益はいくらですか？

 class ValidatedAddrListClass { public: ValidatedAddrListClass(std::vector<Addr> addrs) { if (!valid(addrs)) throw ValidationError {}; } };
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

1. コードはよりモジュール化され安全です。 上記の場合、検証は1回チェックされるアクションであり、後で忘れられます。 すべては誠実さと、 ValidatedAddrListClass
   
   
   
   がある場合、その実装はそこでチェックを行ったという理解に基づいています。 クラスからのこの検証の事実は、特定の値として取り出すことはできません。 何らかのタイプの値の場合、この値はプログラムのさまざまな部分間で転送され、より複雑な値の構築（たとえば、このチェックの拒否）、調査（次の段落を参照）、および通常行われているすべての操作に使用できます値付き。
2. このようなチェックは、（依存）パターンマッチングで使用できます。 確かに、この関数がvalid
   
   
   
   でなく、idrisの場合でも、それは非常に複雑で、idrisは非常に鈍いので、パターンに役立つ情報をvalid
   
   
   
   構造から抽出できます。 それにもかかわらず、 valid
   
   
   
   はやや友好的なパターンマッチングスタイルで書き換えることができますが、これはこの記事の範囲を超えており、通常それ自体は些細なことではありません。

欠点は何ですか？

重大な根本的な欠陥は1つだけvalid



はあまりにも愚かな関数です。 データが検証に合格したかどうかにかかわらず、1ビットの情報のみを返します。 よりスマートなタイプの場合、もっと面白いことができます。

たとえば、アドレスの一意性の要件がTKからなくなったとします。 この場合、既存のアドレスリストに新しいアドレスを追加してもリストが無効にならないことは明らかなので、 So (valid $ types lst) -> So (valid $ types $ addr :: lst)



型の関数を書くことでこの定理を証明できSo (valid $ types lst) -> So (valid $ types $ addr :: lst)



、それを使用して、たとえば、タイプセーフで常に成功するように書く

 insert : (addr : Addr) -> ValidatedAddrList lst -> ValidatedAddrList (addr :: lst)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

しかし、悲しいかな、再帰や帰納法のような定理、そして私たちの問題には優雅な帰納的構造valid



ありません。したがって、私の意見では、 valid



オークブール値を持つコードも悪くありません。