最小アクションの原則。 パート2

前回、私たちは最も注目すべき物理的原理の1つである「最小作用の原理」を簡単に調べ、矛盾するように思われる例に決めました。 この記事では、この原則をより詳細に扱い、この例で何が起こるかを見ていきます。



今回はもう少し数学が必要です。 しかし、私は記事の主要部分を初級レベルでもう一度説明しようとします。 少し厳密で複雑な点を強調しますが、記事の基本的な理解を損なうことなくスキップできます。

境界条件

まず、最も単純なオブジェクト、つまり、力が作用しない空間で自由に動くボールから始めます。 このようなボールは、知られているように、均一かつ直線的に動きます。 簡単にするために、軸に沿って移動すると仮定します $$$x$ ：







その動きを正確に記述するために、原則として、初期条件が設定されます。 たとえば、最初の瞬間に $$$t_A$ ボールはポイントにあった $$$A$ 座標付き $$$x_A$ そして速度があった $$$v_A$ 。 この形式で初期条件を設定した後、ボールのさらなる移動を一意に決定します-一定の速度で移動し、その時点での位置 $$$t$ は、初期位置と速度に経過時間を掛けたものに等しくなります。 $$$x（t）= x_A + v_A \ cdot（t-t_A）$ 。 この初期条件の設定方法は非常に自然で直感的に馴染みがあります。 最初にボールの動きに関する必要な情報をすべて尋ねると、その動きはニュートンの法則によって決定されます。



ただし、これはボールの動きを指定する唯一の方法ではありません。 別の代替方法は、2つの異なる時点でボールの位置を設定することです。 $$$t_A$ そして $$$t_B$ 。 つまり それを尋ねる：



1）時間 $$$t_A$ ボールはポイントにあった $$$A$ （座標付き $$$x_A$ ）;

2）時間 $$$t_B$ ボールはポイントにあった $$$B$ （座標付き $$$x_B$ ）



表現は「ある時点で $$$A$ 「ボールが点で休んだことを意味しない $$$A$ 。 時間に $$$t_A$ 彼はポイントの上を飛ぶことができた $$$A$ 。 それは時間での彼の位置を意味します $$$t_A$ ドットと一致 $$$A$ 。 同じことがポイントにも当てはまります $$$B$ 。



これら2つの条件は、ボールの動きを一意に決定します。 その動きは簡単に計算できます。 両方の条件を満たすために、ボールの速度は明らかに $$$（x_B-x_A）/（t_B-t_A）$ 。 時間のボール位置 $$$t$ 再び、初期位置と速度に経過時間を掛けた値に等しくなります。

$$

$$x（t）= x_A +（（x_B-x_A）/（t_B-t_A））\ cdot（t-t_A）$$

問題の状況では、初期速度を設定する必要がないことに注意してください。 条件1）および2）から一意に決定されます。



2番目の方法で条件を設定するのは異常に見えます。 おそらく一般的にこの形式でそれらを尋ねる必要があるかもしれない理由は明らかではありません。 ただし、最小アクションの原則では、1）と2）の形式の条件が使用され、初期位置と初期速度を設定する形式ではありません。

最小アクション軌道

ここで、ボールの実際の自由な動きから少し脱線し、次の純粋に数学的な問題を考えてみましょう。 任意の方法で手動で移動できるボールがあるとします。 この場合、1）および2）の条件を満たす必要があります。 つまり 間に $$$t_A$ そして $$$t_B$ 私たちはポイントからそれを移動する必要があります $$$A$ ポイントまで $$$B$ 。 これは、まったく異なる方法で実行できます。 このような方法はそれぞれボールの軌道と呼ばれ、ボールの位置の時間の関数によって説明できます。 $$$x（t）$ 。 ボールの位置の時間依存性のグラフで、このような軌道をいくつか延期しましょう。







たとえば、同じ速度でボールを動かすことができます $$$（x_B-x_A）/（t_B-t_A）$ （緑のパス）。 または、半分に保つことができます $$$A$ そして倍速でポイントに移動します $$$B$ （青い軌跡）。 最初に反対方向に動かすことができます。 $$$B$ サイドし、すでにに移動します $$$B$ （茶色の軌跡）。 前後に移動できます（赤い軌跡）。 一般に、条件1）および2）のみが観察される場合は、好きなように移動できます。



そのような軌跡ごとに、番号を一致させることができます。 この例では、つまり ボールに作用する力がない場合、この数値は、次の時間間隔での動きの全時間の合計運動エネルギーに等しい $$$t_A$ そして $$$t_B$ アクションと呼ばれます。

この場合、「蓄積された」運動エネルギーという言葉は意味を正確に伝えません。 実際には、運動エネルギーはどこにも蓄積されず、蓄積は軌道のアクションを計算するためにのみ使用されます。 数学では、そのような蓄積のために非常に良い概念があります-積分：

$$

$$S = \ int \ limits_ {t_A} ^ {t_B} Tdt$$

アクションは通常、文字で示されます $$$S$ 。 記号 $$$T$ 運動エネルギーを意味します。 この積分は、アクションが次の期間のボールの累積運動エネルギーに等しいことを意味します。 $$$t_A$ 前に $$$t_B$ 。

例として、重量1 kgのボールを取り上げましょう。いくつかの境界条件を設定し、2つの異なる軌道のアクションを計算します。 聞かせて $$$B$ ポイントから1メートルです $$$A$ と時間 $$$t_B$ 時間から遠い $$$t_A$ 1秒間。 つまり 最初の瞬間にその地点にあったボールを動かさなければなりません $$$A$ 、1秒で、軸に沿って1 mの距離で $$$x$ 。



最初の例（緑の軌跡）では、ボールを均等に動かしました。 同じ速度で、明らかに次のようになります。 $$$v = 1$ m / s 各瞬間におけるボールの運動エネルギーは次の値に等しくなります： $$$T = mv ^ 2/2$ = 1/2J。1秒で、1/2 Jが蓄積されます。 $$$\ cdot$ 運動エネルギーで。 つまり そのような軌道に有効なのは： $$$S = 1/2$ J $$$\ cdot$ と



さて、すぐにボールをポイントから移さないようにしましょう $$$A$ ポイントまで $$$から$ 、ポイントで0.5秒間保持します $$$A$ 、そして、残りの時間、私たちはそれをポイントに均等に転送します $$$B$ 。 前半では、ボールは静止しており、その運動エネルギーはゼロです。 したがって、軌跡のこの部分のアクションへの寄与もゼロに等しくなります。 後半の2秒間は、ボールを倍速で転送します。 $$$v = 2$ m / s 運動エネルギーは次のようになります $$$T = mv ^ 2/2$ = 2J。この期間のアクションへの寄与は、2 Jに0.5秒を掛けたものになります。 1 J $$$\ cdot$ と したがって、そのような軌道の一般的なアクションは $$$S = 1$ J $$$\ cdot$ と



同様に、境界条件1）および2）が指定された他の軌道には、特定の軌道のアクションに等しい特定の数があります。 このようなすべての軌跡の中で、アクションが最も少ない軌跡があります。 この軌跡が緑の軌跡であることが証明できます。 ボールの均一な動き。 他の軌道については、どんなにトリッキーであっても、アクションは1/2以上になります。



数学では、特定の数の各関数のこのような比較を関数と呼びます。 物理学や数学ではかなり頻繁に、私たちのような問題が発生します。 特定の関数の値が最小であるような関数を見つけるため。 たとえば、数学の発展にとって非常に歴史的に重要な課題の1つは、 バチストクローネの問題です。 つまり ボールが最も速く転がる曲線を見つける。 繰り返しますが、各曲線は関数h（x）で表すことができ、各関数は数値（この場合はボールの転がり時間）に関連付けられています。 繰り返しますが、問題は結局、関数の値が最小の関数を見つけることです。 このような問題を扱う数学の分野は、変動の計算と呼ばれます。

最小アクションの原則

上記の例では、2つの異なる方法で取得された2つの特別な軌道があります。



最初の軌道は物理法則から取得され、力の影響を受けず、境界条件が1）および2）の形式で与えられる、自由なボールの実際の軌道に対応します。



2番目の軌道は、与えられた境界条件1）および2）で軌道を見つける数学的問題から得られます。



最小アクションの原則では、これらの2つの軌道は一致しなければならないと述べています。 つまり、境界条件1）および2）が満たされるようにボールが移動したことがわかっている場合、同じ境界条件の他のパスと比較して、アクションが最小のパスに沿って移動する必要があります。



これは単なる偶然だと考える人もいるかもしれません。 均一な軌道と直線が現れる多くの問題があります。 しかし、最小動作の原理は非常に一般的な原理であり、他の状況、例えば、均一な重力場でのボールの動きに有効です。 これを行うには、運動エネルギーを運動エネルギーと位置エネルギーの差に置き換えるだけです。 この差はラグランジュ関数またはラグランジュ関数と呼ばれ、アクションは累積ラグランジュの合計と等しくなります。 実際、ラグランジュ関数には、システムの動的プロパティに関する必要な情報がすべて含まれています。



点を通過するように均一な重力場でボールを発射した場合 $$$A$ 時間に $$$t_A$ そしてポイントまで飛んだ $$$B$ 時間に $$$t_B$ 、それから彼は、ニュートンの法則に従って放物線を飛行します。 この放物線が、アクションが最小になる軌跡と一致します。

したがって、たとえば地球の重力場などのポテンシャル場で移動する物体の場合、ラグランジュ関数は次のようになります。 $$$L = T（v）-V（x、y、z）$ 。 運動エネルギー $$$T$ 体の速度と電位に依存します-その位置、すなわち 座標 $$$x、y、z$ 。 分析力学では、システムの位置を決定する座標セット全体は通常、1文字で示されます $$$q$ 。 重力場で自由に動くボールの場合、 $$$q$ 座標を意味する $$$x$ 、 $$$y$ そして $$$z$ 。



量の変化率を示すために、物理学では、多くの場合、単にこの量に終止符を打ちます。 例えば $$$\ドットx$ 座標の変化率を示します $$$x$ 、または言い換えれば、方向の体の速度 $$$x$ 。 これらの規則を使用すると、分析力学におけるボールの速度は次のように示されます。 $$$\ドットq$ 。 つまり $$$\ドットq$ 平均速度成分 $$$v_x、v_y、v_z$ 。



ラグランジュ関数は速度と座標に依存するため、明示的に時間に依存することもできます（明示的に時間に依存するとは、値が $$$L$ 異なる時点で、異なる、同じ速度とボールの位置で）一般的な形のアクションは次のように書かれています

$$

$$S = \ int \ limits_ {t_A} ^ {t_B} L（\ dot q、q、t）dt$$

常に最小限ではない

ただし、前のパートの最後で、最小アクションの原則が明らかに機能しない例を見てみました。 これを行うために、力の影響を受けない自由なボールを再び取り、その隣にバネの壁を配置しました。





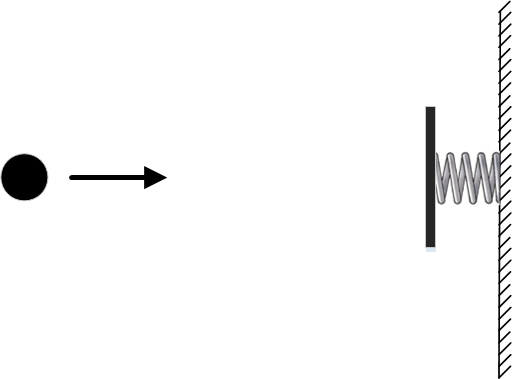
境界条件を設定して、ポイントが $$$A$ そして $$$B$ 一致します。 つまり そして時に $$$t_A$ そして時に $$$t_B$ ボールは同じポイントにある必要があります $$$A$ 。 可能な軌道の1つは、ボールが所定の位置にあることです。 つまり 間の時間間隔全体 $$$t_A$ そして $$$t_B$ 彼はポイントに立って $$$A$ 。 この場合の運動エネルギーと位置エネルギーはゼロに等しくなるため、そのような軌道のアクションもゼロに等しくなります。

厳密に言えば、空間のさまざまなポイントでの位置エネルギーの違いが重要なので、位置エネルギーはゼロではなく任意の数を取ることができます。 ただし、ポテンシャルエネルギーの変化は、最小限のアクションで軌道の検索に影響しません。 すべての軌跡について、アクションの値は同じ数だけ変化し、最小アクションの軌跡は最小アクションの軌跡のままです。 便宜上、ボールにはゼロに等しいポテンシャルエネルギーを選択します。

同じ境界条件を持つ別の可能な物理的軌跡は、ボールが最初に右に飛んで点を通過する軌跡です $$$A$ 時間に $$$t_A$ 。 それから彼はバネと衝突し、それを圧縮し、バネがまっすぐになり、ボールを押し戻し、再び彼はポイントを過ぎて飛びます $$$A$ 。 ボールが壁から跳ね返り、ポイントを飛ぶようにボールの速度を選択できます $$$A$ 今すぐ $$$t_B$ 。 このような軌道を使用したアクションは、基本的にポイント間の飛行中の累積運動エネルギーに等しくなります $$$A$ そして壁と背中。 ボールがスプリングを圧縮し、そのポテンシャルエネルギーが増加する特定の期間があり、この期間中に、ポテンシャルエネルギーがアクションにマイナスの寄与をします。 しかし、そのような期間はそれほど長くなく、アクションは大幅に減少しません。







図は、ボールの物理的に可能な両方の軌道を示しています。 緑のパスは静止しているボールに対応し、青はスプリングの壁から跳ね返るボールに対応しています。



ただし、そのうちの1つだけが最小限の効果、つまり最初の効果しかありません。 2番目の軌道には、より多くのアクションがあります。 この問題には、物理​​的に可能な軌道が2つあり、アクションが最小の軌道が1つしかないことがわかります。 つまり この場合、最小アクションの原則は機能しません。

静止点

ここで何が問題なのかを理解するために、最小アクションの原則から脱却し、通常の機能を取り上げましょう。 いくつかの機能を取りましょう $$$y（x）$ そして彼女のスケジュールを描く：







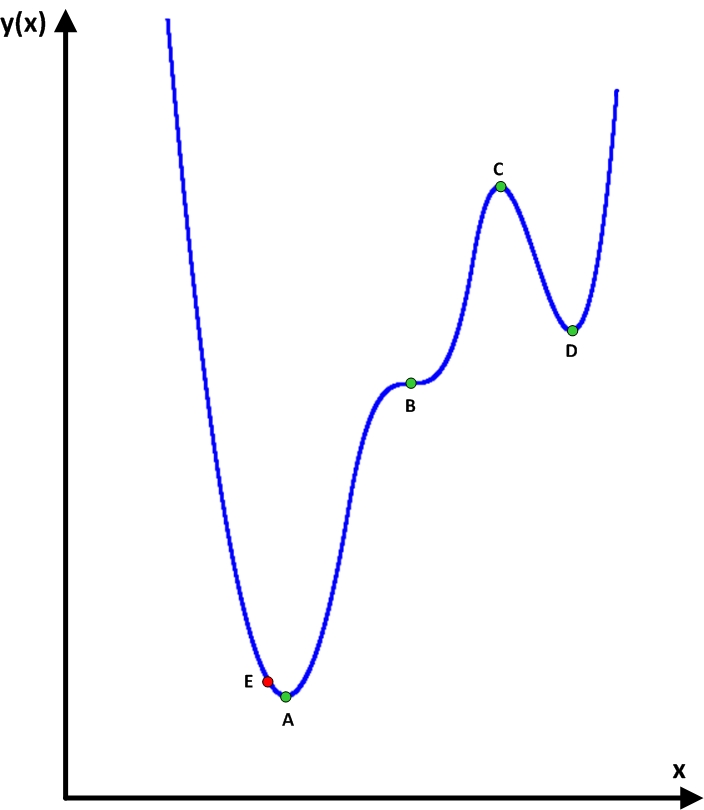
グラフ上で、4つの特別なポイントを緑色でマークしました。 これらのポイントに共通するものは何ですか？ 関数グラフは、ボールが転がることができる実際のスライドであると想像してください。 マークされた4つのポイントは、ボールをこのポイントに正確に取り付けた場合、どこにも転がらないという点で特別です。 他のすべてのポイント、たとえばポイントEでは、彼はその場にとどまることができず、滑り落ち始めます。 そのようなポイントは静止と呼ばれます。 関数の最大値または最小値は、鋭いねじれがない場合、静止点でなければならないため、このような点を見つけることは有用なタスクです。



これらのポイントをより正確に分類する場合、ポイントAは関数の絶対最小値です。 その値は他のどの関数値よりも小さいです。 ポイントB-最大でも最小でもなく、サドルポイントと呼ばれます。 ポイントCは、極大値と呼ばれます。 その値は、関数の隣接点よりも大きくなります。 そして、点Dは極小値、つまり その値は、関数の隣接点よりも小さくなります。



このようなポイントの検索は、数学分析と呼ばれる数学の分野によって実行されます。 別の方法では、それは無限小の量で機能するため、無限小の分析とも呼ばれます。 数学的分析の観点から見ると、静止点には1つの特別な特性があります。 このプロパティが何であるかを理解するには、これらのポイントから非常に短い距離で関数がどのように見えるかを理解する必要があります。 これを行うために、我々は顕微鏡を取り、私たちのポイントでそれを見てください。 この図は、さまざまな倍率でさまざまなポイントの近くで関数がどのように見えるかを示しています。







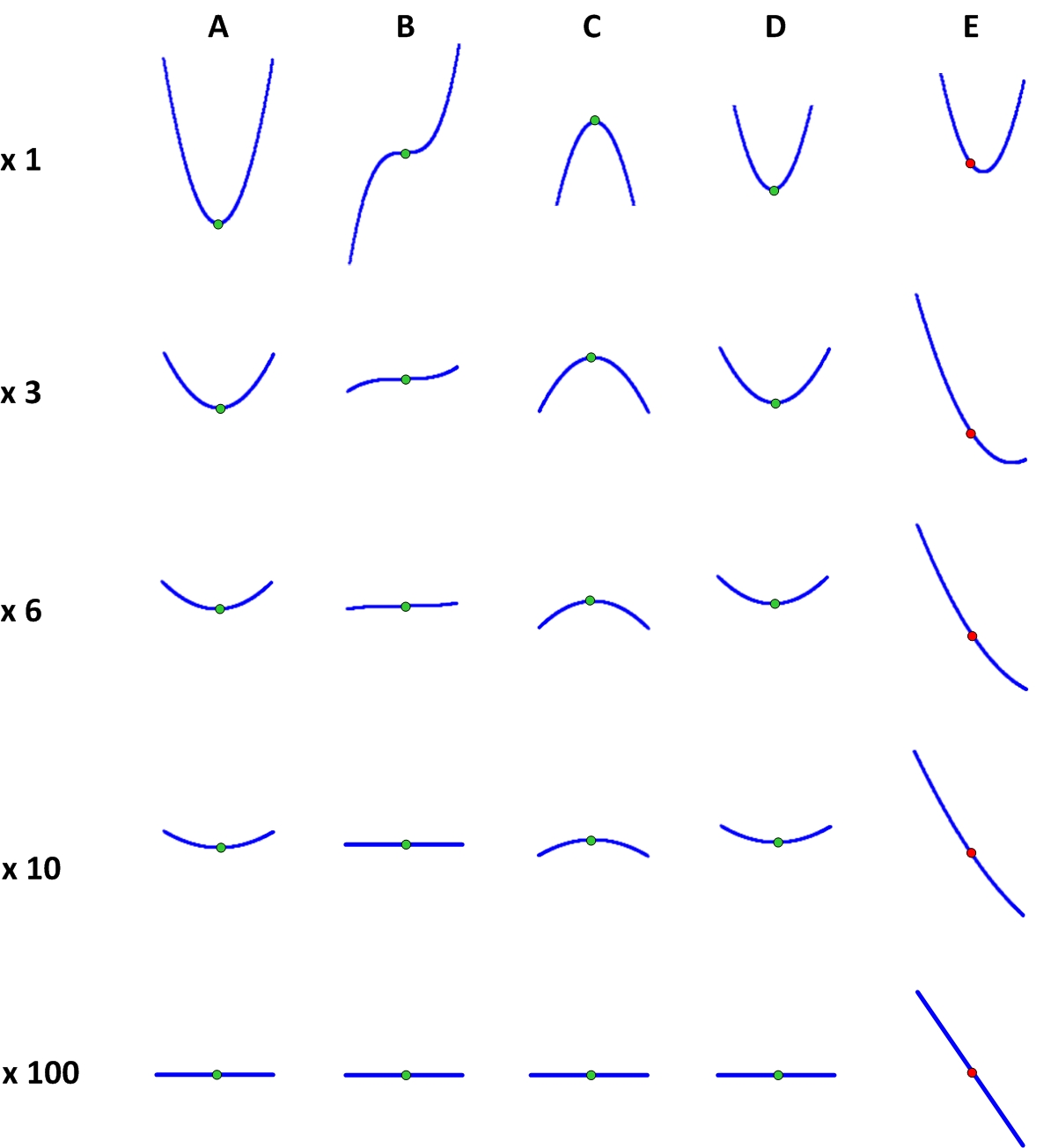
非常に大きな倍率（つまり、非常に小さな偏差x）では、静止点はまったく同じに見え、非静止点とは大きく異なることがわかります。 この違いが何であるかを理解するのは簡単です：増加する静止点での関数のグラフは厳密に水平な線になり、非定常的なものでは傾斜した線になります。 そのため、静止点に取り付けられたボールは転がりません。



静止点での水平関数は別の方法で表現できます。静止点での関数は、その引数の非常に小さな変化で実際に変化しません $$$x$ 、引数自体と比較しても。 関数は小さな変化を伴う非定常点にあります $$$x$ に比例して変化する $$$x$ 。 そして、関数の角度が大きいほど、変更時に関数がより強く変化します $$$x$ 。 実際、サイズが増加する関数は、問題のポイントでグラフの接線にますます類似しています。

厳密な数学言語では、表現は「機能は実際には点で変化しない $$$x_0$ ほとんど変化なし $$$x$ 「機能の変化とその引数の変化の比が $$$Δy/Δx$ で0になる傾向があります $$$∆x$ 0になる傾向があります：

$$ $$表示$$ \ lim_ {Δx\ to 0} \ frac {Δy（x_0）} {Δx} = \ lim_ {x \ to 0} \ frac {y（x_0 +Δx）-y（x_0） } {∆x} = 0 $$表示$$

非固定点の場合、この比率はゼロ以外の数値になる傾向があります。これは、この点での関数の傾斜角の正接に等しくなります。 同じ数は、特定の点での関数の導関数と呼ばれます。 関数の導関数は、引数がわずかに変化するだけで、関数が与えられた点の近くでどれだけ速く変化するかを示します $$$x$ 。 したがって、静止点は、関数の導関数が0になる点です。

静止軌道

静止点との類推により、静止軌道の概念を導入できます。 各軌跡がアクションの特定の値に対応することを思い出してください。 いくつかの番号。 次に、同じ境界条件でそれに近い軌道については、対応するアクション値が実際には静止軌道自体のアクションと変わらないような軌道が存在する可能性があります。 このような軌道は静止と呼ばれます。 言い換えれば、静止軌道に近い軌道は、この静止軌道のアクションとほとんど変わらないアクション値を持ちます。

繰り返しますが、数学言語では「少し違う」という意味は次のとおりです。 機能的なものがあるとしましょう $$$S（x（t））$ 必要な境界条件1）および2）を持つ関数の場合、つまり $$$x（t_A）= A$ そして $$$x（t_B）= B$ 。 軌道を仮定します $$$x（t）$ -静止しています。



私たちは他の機能を取ることができます $$$g（t）$ そのため、最後にゼロの値を取ります。 $$$g（t_A）$ = $$$g（t_B）$ =0。変数も取ります $$$ε$ どんどん少なくしていきます。 これら2つの関数と変数のうち $$$ε$ 3番目の関数を作成できます $$$x '（t）= x（t）+εg（t）$ 、これも境界条件を満たします $$$f '（t_A）= A$ そして $$$f '（t_B）= B$ 。 減少するとき $$$ε$ 関数に対応する軌跡 $$$x '（t）$ 弾道により近くなります $$$x（t）$ 。



さらに、小さな静止軌道の場合 $$$ε$ 軌跡の汎関数の値 $$$x '（t）$ の関数の値とほとんど変わらない $$$x（t）$ と比較しても $$$ε$ 。 つまり

$$ $$表示$$ \ lim_ {ε\ to 0} \ frac {S（x（t））-S（x（t））}ε= \ lim_ {ε\ to 0} \ frac {S（x（ t）+εg（t））-S（x（t））}ε= 0 $$表示$$

これはどのような軌跡にも当てはまりますか $$$g（t）$ 境界条件を満たす $$$g（t_A）$ = $$$g（t_B）$ = 0。



機能の小さな変化を伴う機能の変化（より正確には、機能の変化に比例する機能の変化の線形部分）は、機能の変化と呼ばれ、 $$$δS$ 。 「変動」という用語から、「変動の計算」という名前が付けられます。



静止軌道の場合、関数の変化 $$$δS= 0$ 。



定常関数を見つける方法（最小動作の原理だけでなく、他の多くの問題も）は、オイラーとラグランジュの2人の数学者によって発見されました。 その機能が作用積分に類似した積分によって表される定常関数は、現在オイラー-ラグランジュ方程式と呼ばれている特定の方程式を満たさなければならないことがわかります。

静止原理

軌道のアクションが最小の状況は、機能のアクションが最小の状況に似ています。 軌道の効果が最小になるためには、静止軌道でなければなりません。 ただし、すべての静止軌道が最小動作の軌道であるとは限りません。 たとえば、静止軌道は局所的に最小限のアクションを持つことができます。 つまりその動作は、他の隣接する軌跡の動作よりも小さくなります。ただし、どこか遠くに、アクションがさらに少なくなる他の軌道があるかもしれません。



実際の身体は、必ずしも最小のアクションで軌道に沿って移動するとは限らないことが判明しています。彼らは、より広い一連の特別な軌道、すなわち静止軌道に沿って移動できます。つまり身体の実際の軌道は常に静止しています。したがって、最小アクションの原則は、より正確には静止アクションの原則と呼ばれます。しかし、確立された伝統によれば、それはしばしば最小行動の原則と呼ばれ、これを最小限にするだけでなく、軌道の定常性も暗示します。

通常、教科書に書かれているように、数学言語で定常動作の原理を書き留めることができます。

$$

$$δS=δ\int\limits_{t_A}^{t_B} L(\dot q,q,t)dt = 0$$

。



ここに $$$q$一般化された座標、つまり システムの位置を一意に指定する変数のセット。

$$$\dot q$ -一般化された座標の変化率。

$$$L(\dot q,q,t)$ -ラグランジュ関数。これは一般化された座標、それらの速度、そしておそらく時間に依存します。

$$$S$ -システムの特定の軌道に依存するアクション（つまり、 $$$q(t)$）



システムの実際の軌道は静止しています。彼らのために行動のバリエーション$$$δS=0$ 。

ボールと弾性壁を使用した例に戻ると、この状況の説明は非常に簡単になります。また、ボールが$$$t_A$ そして中に $$$t_B$ 要点をつかむ $$$A$2つの静止軌道があります。そして、ボールはこれらの軌道に沿って本当に動くことができます。軌道の1つを明示的に選択するために、ボールの動きに追加の条件を課すことができます。たとえば、ボールが壁から跳ね返るはずだと言う場合。次に、軌道が一意に決定されます。



最小（より正確には静止）アクションの原則から、次のパートで説明するいくつかのすばらしい結果が得られます。