👌🏻 💕 🙍 Space Engineersでヘキサポッドを構築した方法。パート1 😬 🏅 🌲

こんにちは。 Space Engineersに組み込まれたヘキサポッドの四肢制御システムの設計とプログラミングについてお話したいと思います。

今後は、スペースエンジニアのプログラミングに関連するすべてのものが次の記事に掲載される予定です。この記事では、逆運動学について説明し、アルゴリズムをデバッグしたHTMLキャンバスでプロトタイプを示します。

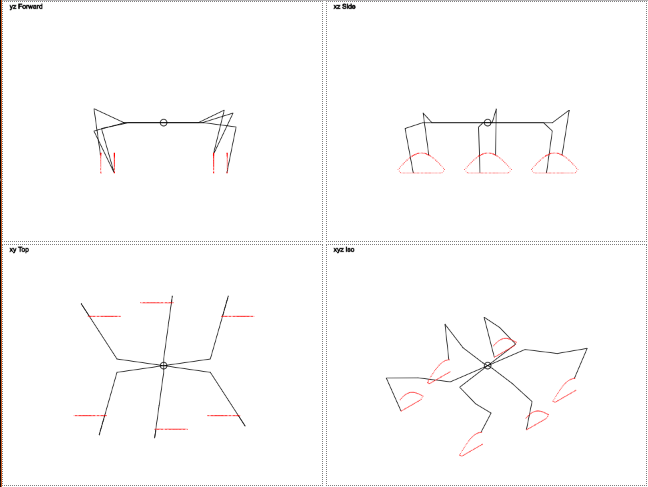
問題の背景と説明。

関節式のシャーシが最初に構築され、その後に掘削ユニットが構築されました。この構成により、すべてのホイールがねじれを含む大きな凹凸の表面と確実に接触しました。

そのように

しかし、車輪がしばしば滑り落ちてしまうため（物理的な問題-ほとんどのブロック（車輪を含む）の摩擦係数が低すぎます）、フィールドに正確に配置することは不可能です。全輪に取り付けられたホイールモジュールを備えたホイール付きプラットフォームは扱いにくいため、物理的な爆発が定期的に発生していました。その結果、最も安定した歩行プラットフォームとして、歩行ロボット、つまりヘキサポッドを構築することが決定されました。

普通の人はどこでヘキサポッドを作り始めますか？彼はおそらくゲームに入り、手足でロボット本体を構築し始め、それからそれをすべて復活させる方法を考えます。しかし、これは私たちの方法ではありません（c）

私は理論から始めました

脚の構造については、次のスキームが選択されました。

内側ジョイント-ヨー軸（ヨー）に沿ってスイングする内側ジョイント

中間ジョイントと外部ジョイント-ピッチの軸（ピッチ）に沿ってスイングする外部ジョイント。基準方向は、足の付け根から足の端までです。

すべてのジョイントの角度が0の場合、脚が完全に伸びていることを意味します（ゲームでまっすぐな脚を構築する方が簡単です）。

タスクは、脚の端が指定されたポイントになるように、指定されたターゲットポイントの関節の回転角度を見つけることです。それは三角法を覚える時間を意味します。

内側のジョイントの角度は、ターゲットの水平座標のアークタンジェントを通して見つけることができます。

const yawRad = Math.atan2(esimatedLegPosition.x, esimatedLegPosition.y);

他の2つのジョイントではさらに困難です。すべてのジョイントの長さがあります。地平線までの角度、中央のジョイントと地面の間の距離、およびターゲットポイントまでの距離を見つけることができます。

次に、余弦定理を使用して、既知の辺の三角形の角度を見つける必要があります。

$画像$

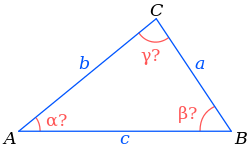
→ 三角形のソリューション

そのため、コードを調べます。

 getLegAngles(esimatedLegPosition) { const yawRad = Math.atan2(esimatedLegPosition.x, esimatedLegPosition.y); const dx = Math.hypot(esimatedLegPosition.x, esimatedLegPosition.y) - this.innerJoint.length; const dz = this.step.idlePosition.z + esimatedLegPosition.z; const hyp = Math.hypot(dx, dz); if (hyp > this.midJoint.length + this.outerJoint.length) {//out of reach hyp = this.midJoint.length + this.outerJoint.length; } const innerAngleRad = Math.acos((this.outerJoint.length * this.outerJoint.length - this.midJoint.length * this.midJoint.length - hyp * hyp) / (-2 * this.midJoint.length * hyp)) + Math.atan2(dz, dx); const outerAngleRad = Math.acos((hyp * hyp - this.midJoint.length * this.midJoint.length - this.outerJoint.length * this.outerJoint.length) / (-2 * this.midJoint.length * this.outerJoint.length)) - Math.PI; return { yaw: yawRad, midPitch: innerAngleRad, outerPitch: outerAngleRad }; }

ムーブメント

次。ロボットは歩く必要がありますよね？つまり、特定の位置の座標を各脚に毎秒N回送信する必要があります。 6本と3本の脚が逆位相で移動することを考えると、どういうわけか難しいことがわかります。新しいレベルの抽象化を導入する必要があります。

しかし、足が円を描いて動き、この円上の位置を示す角度を送信する必要があると想像したらどうでしょうか？サイドへの削除は永続的になり、周期的に変化する1つのパラメーターのみを渡す必要があります。次に、サインとコサインを通してターゲット座標が見つけられます。

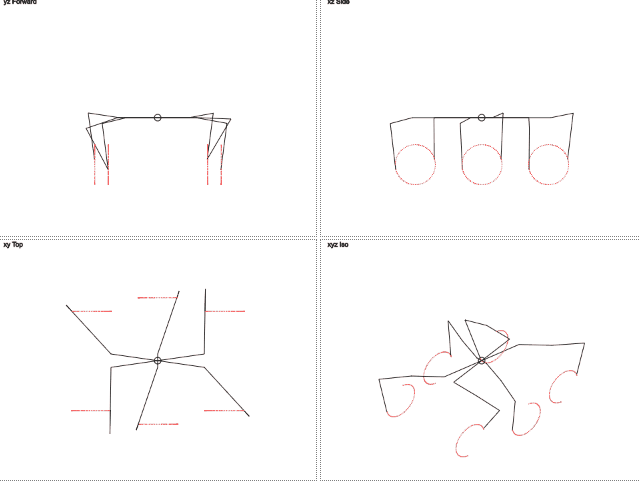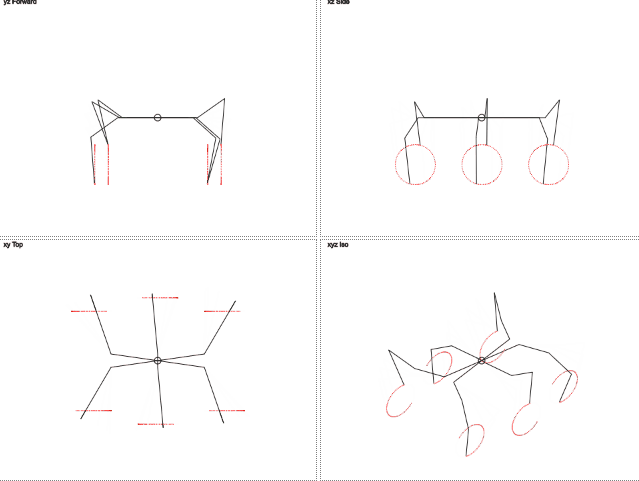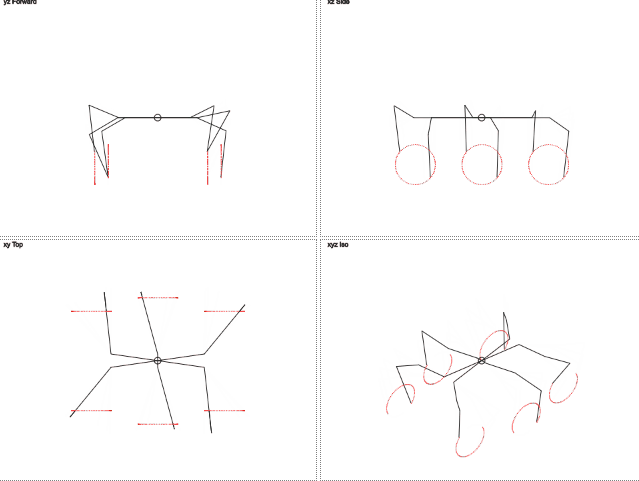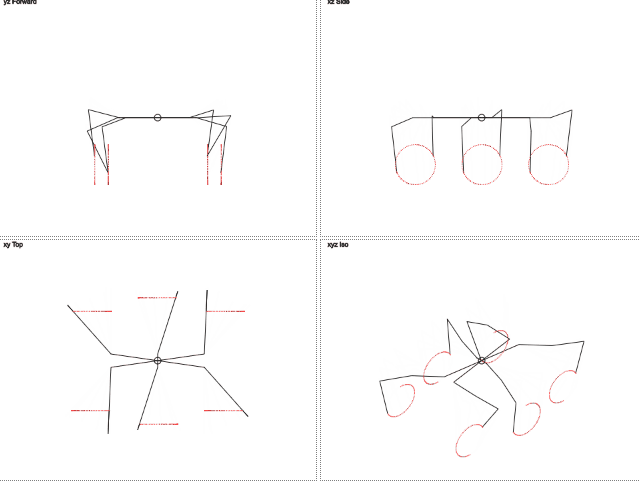
今のところ十分

すべてがどのように機能するかを考えて、タスクが複雑すぎて初めて動作しないことに気づきました（スペースエンジニアのデバッグではすべてが悪いですが、次の部分でさらに詳しく説明します）。

そこで、ビジュアライザーを書くことにしました。ライブラリを追加せずに作成し、ワンクリックで環境を参照せずに実行できるようにしたいと考えました。

したがって、JS + HTML Canvasが選択されました。

フクロウを描いてみましょう。

コード：

ネタバレ見出し

ベクトル：

 class Vector { constructor(x, y, z) { this.x = x; this.y = y; this.z = z; }; distanceTo(vector) { return Math.sqrt(Math.pow(this.x - vector.x, 2) + Math.pow(this.y - vector.y, 2) + Math.pow(this.z - vector.z, 2)); } diff(vector) { return new Vector( this.x - vector.x, this.y - vector.y, this.z - vector.z ); } add(vector) { return new Vector( this.x + vector.x, this.y + vector.y, this.z + vector.z ); } }

ジョイント：

 class Joint { constructor(angle, position, length) { this.angle = angle; this.position = position; this.length = length; this.targetAngle = angle; this.previousAngle = angle; this.velocity = 0; }; setTargetAngle(targetAngle) { this.targetAngle = targetAngle; this.velocity = this.targetAngle - this.normalizeAngle(this.angle); } normalizeAngle(angle) { while (angle <= -Math.PI) angle += Math.PI * 2; while (angle > Math.PI) angle -= Math.PI * 2; return angle; } getCurrentVelocity() {//per tick return this.normalizeAngle(this.angle - this.previousAngle); } tick() { this.previousAngle = this.angle; this.angle = this.angle + this.velocity; } }

ステップ-足を制御するためのデータ構造：

 class Step { constructor( idlePosition,//vector relative to inner joint angle,//step direction length,//step length height,//step height phaseShift// ) { this.idlePosition = idlePosition; this.angle = angle;//radians this.length = length; this.height = height; this.phaseShift = phaseShift; } }

脚：

 class Leg { constructor( vehicleCenter, innerJoint, midJoint, outerJoint, step, phaseStep ) { this.vehicleCenter = vehicleCenter; this.innerJoint = innerJoint; this.midJoint = midJoint; this.outerJoint = outerJoint; this.step = step; this.phaseStep = phaseStep; this.innerJoint.length = innerJoint.position.distanceTo(midJoint.position);//calculate this.midJoint.length = midJoint.position.distanceTo(outerJoint.position);//calculate //this.outerJoint.length = 100; this.joints = [innerJoint, midJoint, outerJoint]; this.preCalculateAngles(); } preCalculateAngles() { this.angles = {}; for (let phase = 0; phase < 360; phase += this.phaseStep) { this.angles[phase] = this.getLegAngles(this.getEsimatedLegPosition(phase, this.step.phaseShift)) } } applyStepHeight(z) { const idleYawRad = Math.atan2(this.step.idlePosition.x, this.step.idlePosition.y); const diffHypot = Math.hypot(this.step.idlePosition.x, this.step.idlePosition.y); const minZ = Math.abs(this.midJoint.length - this.outerJoint.length); const maxZ = (this.midJoint.length + this.outerJoint.length) * 0.6; if (Math.hypot(z, 0) > maxZ) { z = z > 0 ? maxZ : -maxZ; } const safeY = (this.innerJoint.length + this.midJoint.length * 0.5 + this.outerJoint.length * 0.5) * Math.cos(idleYawRad); const vAngle = Math.asin(z / safeY); const y = safeY * Math.cos(vAngle) * Math.cos(idleYawRad); this.step.idlePosition.z = z; this.step.idlePosition.y = this.step.idlePosition.y > 0 ? y : -y; this.preCalculateAngles(); } applyStepAngle(angle) { this.step.angle = angle; this.preCalculateAngles(); } applyPhase(phase/*0-360*/) { const legAngles = this.angles[phase]; this.innerJoint.setTargetAngle(legAngles.yaw); this.midJoint.setTargetAngle(legAngles.midPitch); this.outerJoint.setTargetAngle(legAngles.outerPitch); } getEsimatedLegPosition(phase, phaseShift) { phase = (phase + phaseShift) % 360; const stepX = ((phase < 180 ? phase : 180 - phase % 180) / 180 - 0.5) * this.step.length;//linear movement along step direction const stepZ = Math.max(Math.sin(phase * Math.PI / 180), -0.2) * this.step.height / 1.2; //const stepZ = Math.max((phase > 180 ? Math.cos(phase * Math.PI / 360) + 0.9 : Math.cos((phase - 120) * Math.PI / 360)) * .9 - .1, 0) * this.step.height; const x = this.step.idlePosition.x + stepX * Math.cos(this.step.angle); const y = this.step.idlePosition.y + stepX * Math.sin(this.step.angle); return new Vector(x, y, stepZ); } getLegAngles(esimatedLegPosition) { const yawRad = Math.atan2(esimatedLegPosition.x, esimatedLegPosition.y); const dx = Math.hypot(esimatedLegPosition.x, esimatedLegPosition.y) - this.innerJoint.length; const dz = this.step.idlePosition.z + esimatedLegPosition.z; const hyp = Math.hypot(dx, dz); if (hyp > this.midJoint.length + this.outerJoint.length) {//out of reach hyp = this.midJoint.length + this.outerJoint.length; } const innerAngleRad = Math.acos((this.outerJoint.length * this.outerJoint.length - this.midJoint.length * this.midJoint.length - hyp * hyp) / (-2 * this.midJoint.length * hyp)) + Math.atan2(dz, dx); const outerAngleRad = Math.acos((hyp * hyp - this.midJoint.length * this.midJoint.length - this.outerJoint.length * this.outerJoint.length) / (-2 * this.midJoint.length * this.outerJoint.length)) - Math.PI; if (isNaN(yawRad) || isNaN(innerAngleRad) || isNaN(outerAngleRad)) { console.log(yawRad, innerAngleRad, outerAngleRad); console.log(dx, dz); return; } return { yaw: yawRad, midPitch: innerAngleRad, outerPitch: outerAngleRad }; } getMaxMinAngles() { const angles = [0, 90, 180, 270].map((phase) => { return this.getLegAngles(getEsimatedLegPosition(phase, 0)); }); return { yawMin: Math.min(angles.map((x) => { return x.yaw })), yawMax: Math.max(angles.map((x) => { return x.yaw })), midPitchMin: Math.min(angles.map((x) => { return x.midPitch })), midPitchMax: Math.max(angles.map((x) => { return x.midPitch })), outerPitchMin: Math.min(angles.map((x) => { return x.outerPitch })), outerPitchMax: Math.max(angles.map((x) => { return x.outerPitch })), } } tick() { this.joints.forEach(function (joint) { joint.tick(); }); } getVectors() { const res = []; const sinYaw = Math.sin(this.innerJoint.angle); const cosYaw = Math.cos(this.innerJoint.angle); let currentVector = this.vehicleCenter; res.push(currentVector); currentVector = currentVector.add(this.innerJoint.position); res.push(currentVector); currentVector = currentVector.add(new Vector( this.innerJoint.length * sinYaw, this.innerJoint.length * cosYaw, 0 )); res.push(currentVector); const dxMid = Math.cos(this.midJoint.angle) * this.midJoint.length; const dzMid = Math.sin(this.midJoint.angle) * this.midJoint.length; currentVector = currentVector.add(new Vector( dxMid * sinYaw, dxMid * cosYaw, dzMid )); res.push(currentVector); const c = this.midJoint.angle + this.outerJoint.angle; const dxOuter = Math.cos(c) * this.outerJoint.length; const dzOuter = Math.sin(c) * this.outerJoint.length; currentVector = currentVector.add(new Vector( dxOuter * sinYaw, dxOuter * cosYaw, dzOuter )); res.push(currentVector); return res; } }

ロボット：

 class Hexapod { constructor(phaseStep) { this.idleHeight = -70; this.stepAngle = 0; this.turnAngle = 0; this.stepLength = 70; this.stepHeight = 30; this.debugPoints = []; const vehicleCenter = new Vector(0, 0, 0); this.legs = [ new Leg( vehicleCenter, new Joint(0, new Vector(-70, 10, 0), 50), new Joint(0, new Vector(-70, 60, 0), 50), new Joint(0, new Vector(-70, 110, 0), 70), new Step(new Vector(-30, 90, this.idleHeight), this.stepAngle, this.stepLength, this.stepHeight, 0), phaseStep ), new Leg( vehicleCenter, new Joint(0, new Vector(-70, -10, 0), 50), new Joint(0, new Vector(-70, -60, 0), 50), new Joint(0, new Vector(-70, -110, 0), 70), new Step(new Vector(-30, -90, this.idleHeight), this.stepAngle, this.stepLength, this.stepHeight, 180), phaseStep ), new Leg( vehicleCenter, new Joint(0, new Vector(0, 10, 0), 50), new Joint(0, new Vector(0, 60, 0), 50), new Joint(0, new Vector(0, 110, 0), 70), new Step(new Vector(0, 100, this.idleHeight), this.stepAngle, this.stepLength, this.stepHeight, 180), phaseStep ), new Leg( vehicleCenter, new Joint(0, new Vector(0, -10, 0), 50), new Joint(0, new Vector(0, -60, 0), 50), new Joint(0, new Vector(0, -110, 0), 70), new Step(new Vector(0, -100, this.idleHeight), this.stepAngle, this.stepLength, this.stepHeight, 0), phaseStep ), new Leg( vehicleCenter, new Joint(0, new Vector(70, 10, 0), 50), new Joint(0, new Vector(70, 60, 0), 50), new Joint(0, new Vector(70, 110, 0), 70), new Step(new Vector(30, 90, this.idleHeight), this.stepAngle, this.stepLength, this.stepHeight, 0), phaseStep ), new Leg( vehicleCenter, new Joint(0, new Vector(70, -10, 0), 50), new Joint(0, new Vector(70, -60, 0), 50), new Joint(0, new Vector(70, -110, 0), 70), new Step(new Vector(30, -90, this.idleHeight), this.stepAngle, this.stepLength, this.stepHeight, 180), phaseStep ), ]; } applyPhase(phase/*0-360*/) { this.legs.forEach(function (leg) { leg.applyPhase(phase); }); } changeHeight(value) { this.legs.forEach(function (leg) { leg.applyStepHeight(this.idleHeight + value); }, this); } changeStepLength(value) { this.stepLength += value; this.legs.forEach(function (leg) { leg.step.length = this.stepLength; leg.preCalculateAngles(); }, this); } applyTurn1(centerX, centerY) { const angleToAxis = Math.atan2(centerX, centerY); const distanceToAxis = Math.hypot(centerX, centerY); distanceToAxis = 1000/distanceToAxis; this.legs.forEach(leg => { const dx = leg.step.idlePosition.x + leg.innerJoint.position.x + Math.sin(angleToAxis)*distanceToAxis || 0; const dy = leg.step.idlePosition.y + leg.innerJoint.position.y + Math.cos(angleToAxis)*distanceToAxis || 0; const angle = Math.atan2(dy,dx); const hypIdle = Math.hypot(dx, dy); leg.applyStepAngle(angle+Math.PI/2); leg.step.length = this.stepLength *hypIdle/ ((distanceToAxis || 0) + 1000); }); } applyTurn(centerX, centerY) { this.stepAngle = Math.atan2(centerX, centerY); if (this.stepAngle > Math.PI / 2) this.stepAngle -= Math.PI; if (this.stepAngle < -Math.PI / 2) this.stepAngle += Math.PI; const mults = this.legs.map(leg => Math.hypot(leg.step.idlePosition.y + leg.innerJoint.position.y, leg.step.idlePosition.x + leg.innerJoint.position.x) / Math.hypot(leg.step.idlePosition.y + leg.innerJoint.position.y + centerY*.3, leg.step.idlePosition.x + leg.innerJoint.position.x + centerX*.3)); const minMult = Math.min(...mults); const maxMult = Math.max(...mults); const mult = minMult / maxMult; const d = Math.pow(Math.max(...this.legs.map(leg =>Math.hypot(leg.step.idlePosition.y + leg.innerJoint.position.y, leg.step.idlePosition.x + leg.innerJoint.position.x))),2)/Math.hypot(centerX,centerY); const a = Math.atan2(centerX,centerY); this.legs.forEach(leg => { const dx = leg.step.idlePosition.x + leg.innerJoint.position.x; const dy = leg.step.idlePosition.y + leg.innerJoint.position.y; const idleAngle = Math.atan2(dx, dy) + this.stepAngle; const turnAngle = Math.atan2(dx + centerX, dy + centerY); const hypIdle = Math.hypot(dx, dy); const hyp = Math.hypot(dx + centerX, dy + centerY); leg.applyStepAngle(turnAngle - idleAngle); leg.step.length = this.stepLength * hyp / hypIdle * mult; }); this.debugPoints = [new Vector(Math.sin(a)*-d,Math.cos(a)*-d,0)]; } tick() { this.legs.forEach(function (leg) { leg.tick(); }); } getVectors() { return this.legs.map(function (leg) { return leg.getVectors() }); } }

ただし、描画するには、さらにいくつかのクラスが必要です。

キャンバスにラップする：

 class Canvas { constructor(id, label, axisSelectorX, axisSelectorY) { const self = this; this.id = id; this.label = label; this.canvas = document.getElementById(id); this.ctx = this.canvas.getContext('2d'); this.axisSelectorX = axisSelectorX; this.axisSelectorY = axisSelectorY; this.canvasHeight = this.canvas.offsetHeight; this.canvasWidth = this.canvas.offsetWidth; this.initialY = this.canvasHeight / 2; this.initialX = this.canvasWidth / 2; this.traceCounter = 0; this.maxTraces = 50; this.traces = {}; const axisSize = 150; this.axisVectors = [ [ new Vector(-axisSize, -axisSize, -axisSize), new Vector(-axisSize, -axisSize, axisSize) ], [ new Vector(-axisSize, -axisSize, -axisSize), new Vector(-axisSize, axisSize, -axisSize) ], [ new Vector(-axisSize, -axisSize, -axisSize), new Vector(axisSize, -axisSize, -axisSize) ], ] this.mouseOver = false; this.mousePos = { x: 0, y: 0 };//relative to center this.clickPos = { x: 0, y: 0 };//relative to center this.canvas.addEventListener("mouseenter", function (event) { self.mouseOver = true; }, false); this.canvas.addEventListener("mouseleave", function (event) { self.mouseOver = false; }, false); this.canvas.addEventListener("mousemove", function (event) { if (self.mouseOver) { self.mousePos = { x: event.offsetX - self.initialX, y: event.offsetY - self.initialY }; } }, false); this.canvas.addEventListener("mouseup", function (event) { if (self.mouseOver) { self.clickPos = { x: event.offsetX - self.initialX, y: event.offsetY - self.initialY }; } }, false); }; clear(drawAxis) { this.ctx.clearRect(0, 0, this.canvasWidth, this.canvasHeight); this.ctx.strokeStyle = "#000000"; this.ctx.strokeText(this.label, 10, 10); if (drawAxis) { this.axisVectors.forEach(function (vectors, i) { this.ctx.moveTo(this.initialX, this.initialY); this.ctx.beginPath(); vectors.forEach(function (vector) { this.ctx.lineTo(this.initialX + this.axisSelectorX(vector), this.initialY - this.axisSelectorY(vector)); }, this); this.ctx.stroke(); const lastVector = vectors[vectors.length - 1]; this.traces[[this.traceCounter, i]] = lastVector }, this); } } drawVectors(vectors) {/*2d array*/ vectors.forEach(function (vectors, i) { this.ctx.moveTo(this.initialX, this.initialY); this.ctx.beginPath(); vectors.forEach(function (vector) { this.ctx.lineTo(this.initialX + this.axisSelectorX(vector), this.initialY - this.axisSelectorY(vector)); }, this); this.ctx.stroke(); const lastVector = vectors[vectors.length - 1]; this.traces[[this.traceCounter, i]] = lastVector }, this); for (const key in this.traces) { const vector = this.traces[key]; this.ctx.fillStyle = "#FF0000";//red this.ctx.fillRect(this.initialX + this.axisSelectorX(vector), this.initialY - this.axisSelectorY(vector), 1, 1); } this.ctx.strokeStyle = "#000000"; this.ctx.beginPath(); this.ctx.arc(this.clickPos.x + this.initialX, this.clickPos.y + this.initialY, 5, 0, 2 * Math.PI); this.ctx.stroke(); if (this.mouseOver) { this.ctx.strokeStyle = "#00FF00"; this.ctx.beginPath(); this.ctx.arc(this.mousePos.x + this.initialX, this.mousePos.y + this.initialY, 10, 0, 2 * Math.PI); this.ctx.stroke(); } this.traceCounter = (this.traceCounter + 1) % this.maxTraces; } drawPoints(points) { this.ctx.fillStyle = "#00ff00";//green points.forEach(function (point) { this.ctx.fillRect(this.initialX + this.axisSelectorX(point), this.initialY - this.axisSelectorY(point), 3, 3); }, this); } }

Legクラスには、ジョイントの現在の座標を取得するためのメソッドがあります。これらは描画する座標です。

そのため、足が最後のNティックにあるポイントの描画も追加しました。

そして最後に、シミュレーションを実行するワーカー：

 class Worker { constructor(tickTime) { const self = this; this.phaseStep = 5; this.tickTime = tickTime; const tan30 = Math.tan(Math.PI / 6); const scale = 0.7; this.canvases = [ new Canvas('canvasForward', 'yz Forward', function (v) { return vy }, function (v) { return vz }), new Canvas('canvasSide', 'xz Side', function (v) { return vx }, function (v) { return vz }), new Canvas('canvasTop', 'xy Top', function (v) { return vx }, function (v) { return -vy }), new Canvas('canvasIso', 'xyz Iso', function (v) { return vx * scale + vy * scale }, function (v) { return vz * scale + vx * tan30 * scale - vy * tan30 * scale }), ]; this.bot = new Hexapod(this.phaseStep); this.phase = 0; this.focus = true; window.addEventListener('focus', function () { console.log('focus'); self.focus = true; }); window.addEventListener('blur', function () { console.log('blur'); self.focus = false; }); this.start(); } tick(argument) { const canvasForward = this.canvases[0]; const bot = this.bot; if (canvasForward.mouseOver) { bot.changeHeight(-canvasForward.mousePos.y); } else { bot.changeHeight(0); } const canvasTop = this.canvases[2]; if (canvasTop.mouseOver) { bot.applyTurn(-canvasTop.mousePos.x, -canvasTop.mousePos.y); } else { bot.applyTurn(0, 0); } this.phase = (this.phase + this.phaseStep) % 360; bot.applyPhase(this.phase); bot.tick(); const vectors = bot.getVectors(); this.canvases.forEach(function (c) { c.clear(false); c.drawVectors(vectors); c.drawPoints(bot.debugPoints); }); } start() { this.stop(); this.interval = setInterval((function (self) { return function () { if (self.focus) { self.tick(); } } })(this), this.tickTime); } stop() { clearInterval(this.interval); } }

結果：

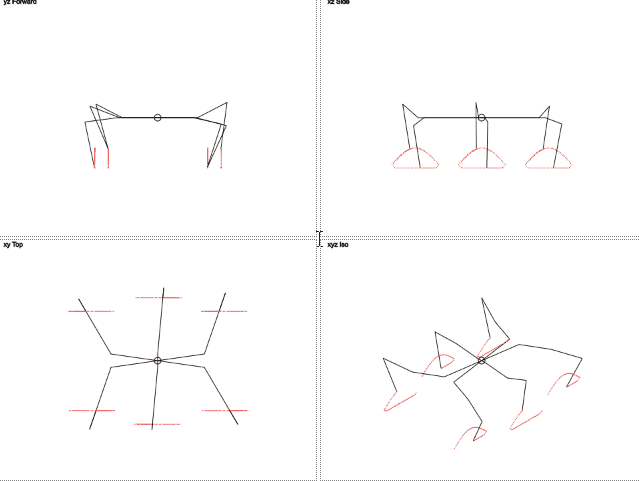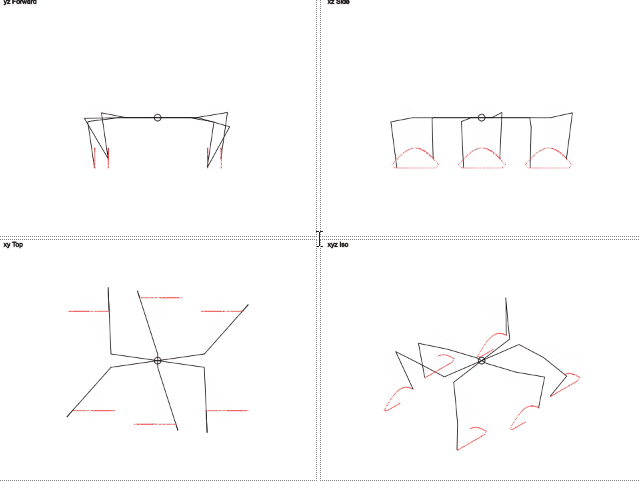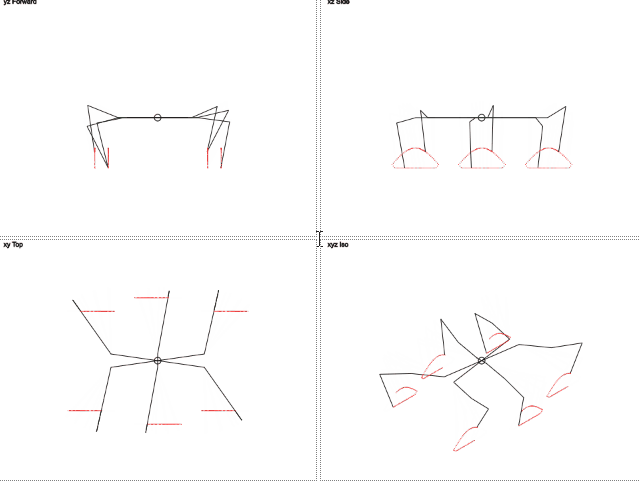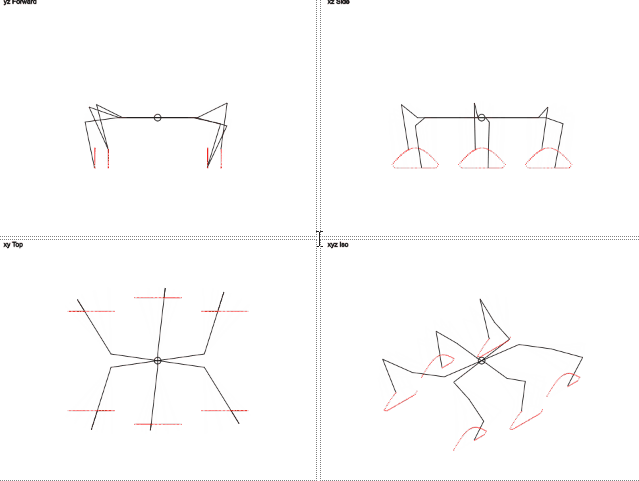
本当にいい？

ここでは、脚の軌道が円と異なることがわかります。垂直方向の動きはトリミングされた正弦波に似ており、水平方向の動きは直線的です。これにより、脚への負荷が軽減されます。

ここで、コードで何が起こっているのかをいくつか説明します。

ロボットに方向転換を教える方法は？

回すために、私は2つの状況を見ました：

ロボットが立っている場合、脚は円を描くように動きます。

しかし、唯一のこと-円の周りの動きは、現在の実装でコードを大きく複雑にします。したがって、脚は円の接線方向に移動します。

ロボットが移動するとき、アッカーマンステアリングジオメトリのようなものを差動で実装する必要があります。

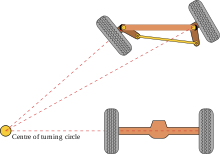
つまり、より小さい半径に沿って移動する脚のステップ長は短くなります。そして、回転角度が大きくなります。

各脚の回転角度の変更を実装するために、次のアルゴリズムを思いつきました。

1.脚の初期位置からロボットの中心までの角度を考慮します。

 const idleAngle = Math.atan2(dx, dy) + this.stepAngle;

2.脚の初期位置から（ロボットの中心+回転の原因となるオフセットは可変パラメーターです）までの角度を考慮します。

 const turnAngle = Math.atan2(dx + centerX, dy + centerY);

3.ステップをこれらの角度の差に向けます。

 leg.applyStepAngle(turnAngle - idleAngle);

しかし、それだけではありません。それでも歩幅を変更する必要があります。額の実現-中心までの距離を変更することでステップの長さを増やす-致命的な欠陥がありました-外側の足があまりにも広く歩き、お互いを傷つけ始めました。

したがって、実装を複雑にする必要がありました。

1.各脚の中心までの距離の変化を考慮します。

 const mults = this.legs.map(leg => Math.hypot(leg.step.idlePosition.y + leg.innerJoint.position.y, leg.step.idlePosition.x + leg.innerJoint.position.x) / Math.hypot(leg.step.idlePosition.y + leg.innerJoint.position.y + centerY*.3, leg.step.idlePosition.x + leg.innerJoint.position.x + centerX*.3));

0.3-マジックナンバー

2.最小変化と最大変化の関係を見つける

 const minMult = Math.min(...mults); const maxMult = Math.max(...mults); const mult = minMult / maxMult;

この係数は、中心までの距離の最小変化と最大変化の差を反映しています。それは常に1未満であり、ステップ長にそれを掛けると、回転方向の外側にある脚でも回転しても増加しません。

 const hypIdle = Math.hypot(dx, dy); const hyp = Math.hypot(dx + centerX, dy + centerY); leg.step.length = this.stepLength * hyp / hypIdle * mult;

仕組みは次のとおりです（gif 2メガバイト）：

gif 2メガバイト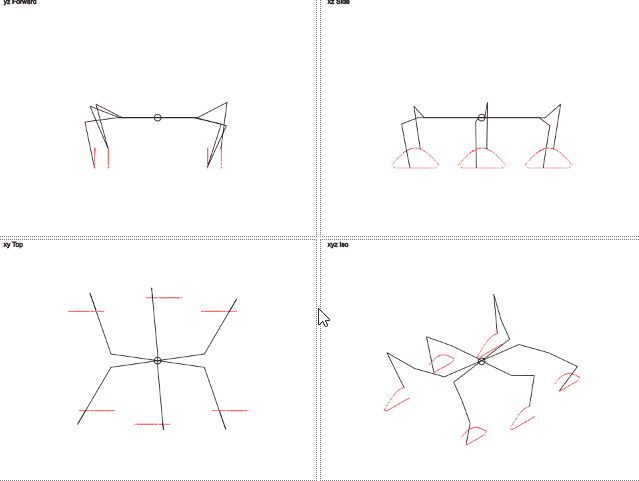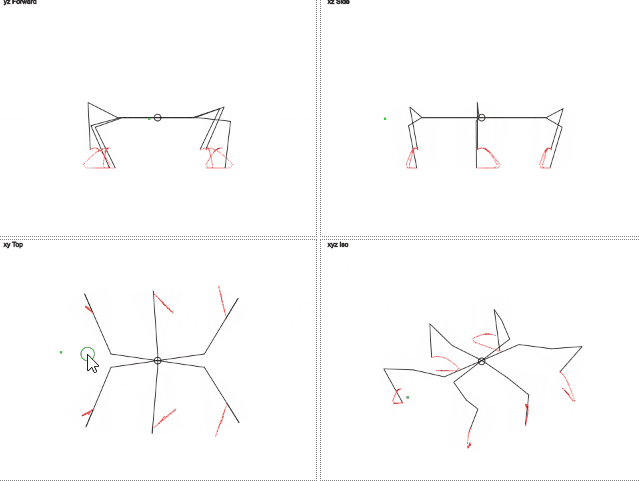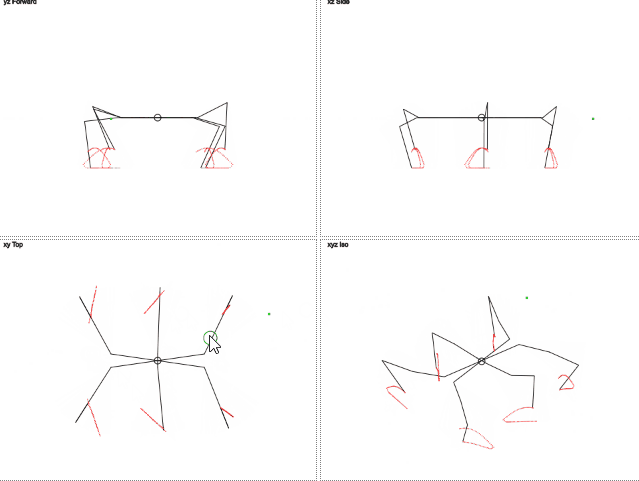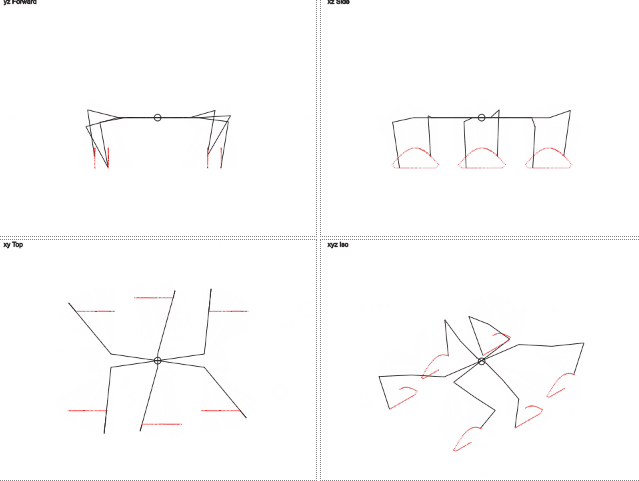

→ ここで結果を試すことができます

よく見ると、コンテンツをhtmlファイルに保存し、お気に入りのテキストエディターで続行することをお勧めします。

次の投稿では、このすべてを宇宙エンジニアでどのように作成したかを説明します。

ネタバレ：Programmable Blockでは、C＃でほぼ最新バージョンを書くことができます。

Space Engineersでヘキサポッドを構築した方法。 パート1

問題の背景と説明。

私は理論から始めました

ムーブメント

ロボットに方向転換を教える方法は？

More articles:

Space Engineersでヘキサポッドを構築した方法。パート1