はじめに
酸化剤タンクと燃料タンクからの燃料は、ロケットエンジンの燃焼室に入ります。 所定の割合での同期燃料供給により、ロケットエンジンの効率的な動作が保証されます。
効率的な操作は、タンク内の燃料レベルの正確な測定に依存します。 この目的のために、燃料タンクには燃料管理システムがあります。 このシステムは、チャンネル内の自由液面を固定するためのセンサーをチャンネル内に備えた垂直測定チャンネルです[1]。
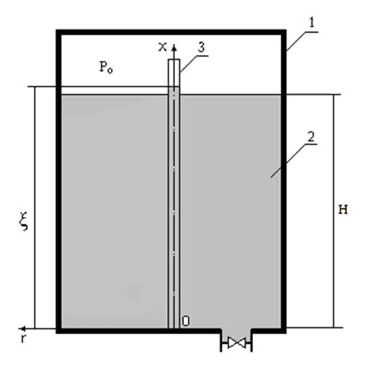
描画。 燃料タンクのスキーム。 1-タンク、2-燃料、3-測定チャネル、Po-ガス圧、
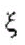-チャンネル内の液体レベル、H-タンク内の液体レベル、r、x-座標軸。
垂直チャネルと燃料タンクは通信する容器です。 タンク内の燃料レベルが低下すると、測定チャネル内の燃料レベルも低下します。 チャンネル内の燃料レベルがセンサーに達すると、センサーが作動します。 信号は燃料管理システムに入ります。
燃料消費の結果として、タンク内のレベルが変化します。 したがって、チャネル内の燃料レベルは、タンク内の燃料レベルを決定する必要があります。 2つの問題があります。 最初の方法論は、タンク内の燃料の自由表面がチャネル内の燃料の表面と一致しないことです。
2番目の問題は、飛行中のロケットの加速度を変更する際のレベルの変動であり、センサーの誤警報につながり、その結果、測定エラーにつながります。
燃料レベルの測定エラーは、非効率的な燃料消費につながります。 その結果、ロケットエンジンは最適に動作せず、「過剰な」燃料がタンク内に残る可能性があります。
次に、最初の問題から方法論的誤差を決定し、2番目の問題から測定誤差を減らす方法を検討します。
読者をリンク[1]に送らないようにするため、ここでは測定チャネル内の流体運動の微分方程式の導出を行い、同時に数学的および文法的なエラーを修正します。
飛行tの間、燃料タンク内の液体レベルHは比率に従って変化します。
（1）
ここで：–タンク内の初期燃料レベル。 V –燃料レベルの変化率。
座標系を導入すると（図を参照）、測定チャネル内の粘性のある非圧縮性流体の非定常運動の方程式は次のようになります。
（2）
境界でそしてプライマリ
条件。
ここで、u（r、t）はチャネル内の流体速度です。 pは圧力です。 ρは密度です。 時間はtです。 vは動粘度です。 g-重力の加速。
測定チャネルの平均速度の比率を取得します。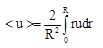
式（2）の左辺と右辺にrを掛けて、運動方程式の個々の項を記述します。
（3）
ここで：摩擦;
壁摩擦;
動的粘度; Rは、円筒形チャネルの半径です。
式（3）を使用し、式（2）を次の形式で記述します（以降、平均速度の斜角括弧は省略します）。
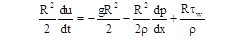
または
（4）
円筒形の流路で、距離を置いた2つの断面の液体の体積を選択します。 選択したボリュームの圧力と摩擦のバランスを書きます。
比率を取得します。
（5）
Darcy-Weisbach方程式を使用します（5）と組み合わせると、次のようになります。
ここから、測定チャネルの壁に対する流体摩擦の比率は次の形式になります。
（6）
ここで、λは油圧摩擦係数です。
式（4）に（6）を代入して、次の式を取得します。
（7）
以下の条件下で圧力勾配を計算します。圧力は、燃料の自由表面上のブースト圧力から圧力まで直線的に減少します。 （1）を考慮した圧力勾配は次のようになります。
（8）
（8）を関係（7）に代入すると、測定チャネルの液体レベルの最終微分方程式が得られます。
（9）
次の形式の初期コーシー条件を使用します。
（10）
初期条件（10）で微分方程式（9）を解きます[2]。
式（9）の解を使用して測定情報を処理する方法を選択するために、ロケットの燃料タンク内の液体レベルを測定する条件を検討します
a）測定チャネルにノイズや燃料の変動がない場合のレベル測定。 レベル測定の結果のロケットの飛行時間への依存性は、次のプログラムを使用して決定されます。
# -*- coding: utf8 -*- import numpy as np from scipy.integrate import odeint import matplotlib.pyplot as plt R=0.0195 # H=8.2# , g=9.8# /2 L=4.83*10**-2# V=0.039# / def f(y,t): y1,y2=y return [y2,-g+(g*(HV*t)/y1)+((L/(4*R))*y2**2)] t = np.arange(0,10,0.01) y0=[H,0] [y1,y2]=odeint(f,y0,t,full_output=False).T plt.title(' ') plt.ylabel('H,m') plt.xlabel('t,s') plt.plot(t,y1,"b",linewidth=2,label=' ') y=HV*t plt.plot(t,y,"--r",linewidth=2,label=' ') plt.grid(True) plt.legend(loc='best') plt.show()
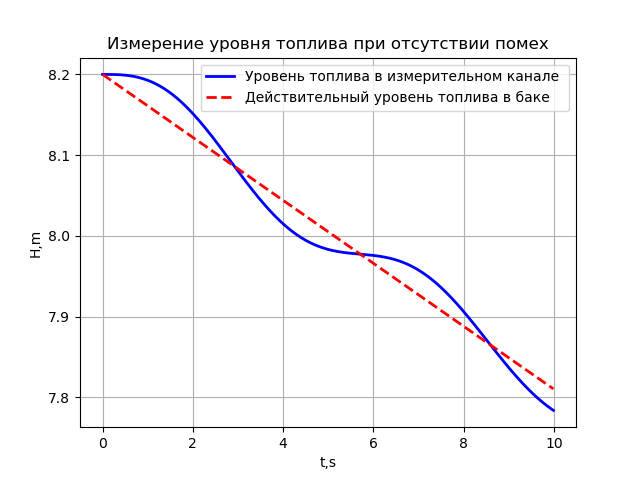
これは、測定チャネルのレベルがタンクのレベルよりも遅れている場合の最初の問題（卒業による）に対する明らかな解決策です。 実際の動作条件では、レベルの変動とセンサーのノイズが測定に大きな誤差をもたらすためです。
b）分散0.1の正規分布ランダム振動とノイズの条件下でのレベル測定。 レベル測定の結果のロケットの飛行時間への依存性は、次のプログラムを使用して決定されます。
# -*- coding: utf8 -*- import numpy as np from scipy.integrate import odeint import matplotlib.pyplot as plt R=0.0195 # H=8.2# , g=9.8# /2 L=4.83*10**-2# V=0.039# / def f(y,t): y1,y2=y return [y2,-g+(g*(HV*t)/y1)+((L/(4*R))*y2**2)] t = np.arange(0,10,0.01) y0=[H,0] [y1,y2]=odeint(f,y0,t,full_output=False).T y1= np.array([np.random.normal(x,0.1) for x in y1])# plt.title(' \n 0.1') plt.ylabel('H,m') plt.xlabel('t,s') plt.plot(t,y1,"b",linewidth=2,label=' ') y=HV*t plt.plot(t,y,"--r",linewidth=2,label=' ') plt.grid(True) plt.legend(loc='best') plt.show()
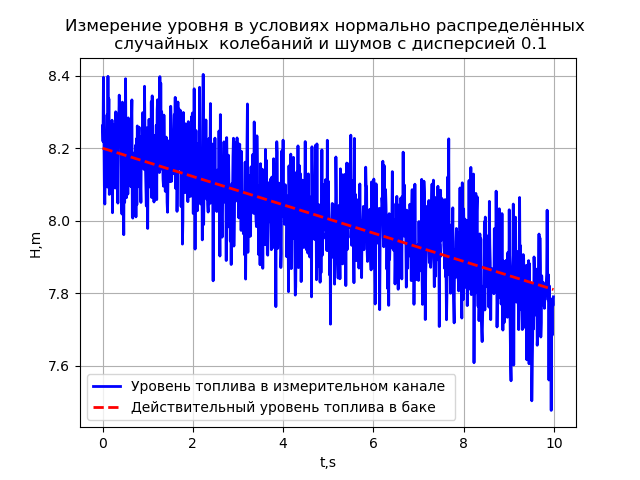
上記の結果は、範囲の数パーセントの許容誤差があるこのような条件でのレベル測定は不可能であるという結論を確認します。
d）カルマンフィルターを使用した、0.1の分散を伴う正規分布ランダム振動とノイズの条件下でのレベル測定。 レベル測定の結果のロケットの飛行時間への依存性は、次のプログラムを使用して決定されます。
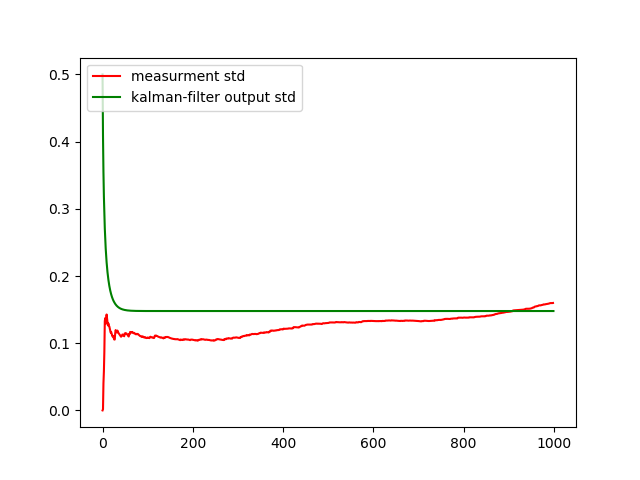
# -*- coding: utf8 -*- from scipy.integrate import odeint import matplotlib.pyplot as plt from numpy import* from pykalman import KalmanFilter R=0.0195 H=8.2 g=9.8 L=4.83*10**-2 V=0.039 def f(y,t): y1,y2=y return [y2,-g+(g*(HV*t)/y1)+((L/(4*R))*y2**2)] t = arange(0,10,0.01) y0=[H,0] [y1,y2]=odeint(f,y0,t,full_output=False).T y=array(HV*t)# measurements = array([random.normal(x,0.1) for x in y1]) kf = KalmanFilter(transition_matrices=[1] ,# observation_matrices=[1],# initial_state_mean=measurements[0],# initial_state_covariance=1,# observation_covariance=1,# transition_covariance= 0.001) # state_means, state_covariances = kf.filter(measurements)# , state_std = sqrt(state_covariances[:,0]) plt.figure() plt.title(' ') plt.ylabel('H,m') plt.xlabel('t,s') plt.plot(measurements, '-r', label=' ') plt.plot(state_means, '-g', label='kalman- ') plt.plot(y, '-k', label=' ') plt.legend(loc='best') plt.figure() measurement_std = [std(measurements[:i]) for i in arange(1,len(measurements),1)] plt.plot(measurement_std, '-r', label='measurment std') plt.plot(state_std, '-g', label='kalman-filter output std') plt.legend(loc='upper left') plt.show()
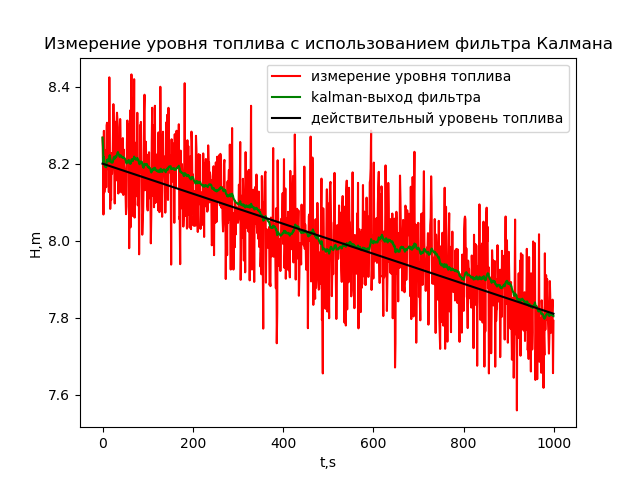
グラフからわかるように、フィルターはランダム成分を除去し、値を平均しました。 ただし、カルマンフィルターは「さらに賢く」、特定の設定で方法論的なエラーを減らすことさえできます。
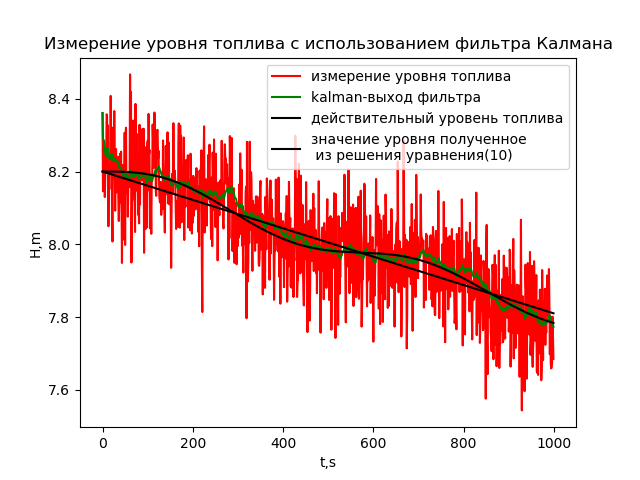
結論
分散が0.1のセンサーのレベルとノイズの正規分布ランダム変動下でのロケットの燃料タンク内の液体レベルの測定は、 カルマンフィルターを使用してのみ可能です。
参照資料
1. ロケットの燃料タンク内の液体レベルの測定 。
2. 航空機の船外燃料タンク 。