科学情報学の学習のためのPython：キューイングシステムのモデリング

注釈

この記事では、トレーニングのモデリングに基づいた科学情報学の初期開発の方法論を紹介します。 調査中のオブジェクトの基盤として、マルチフェーズキューイングシステムを提供しています。 Pythonと並列コンピューティングを使用してモデルを実装し、プログラムコードと確率的モデリングの結果を提供します。

1.はじめにと背景

私たちの研究では、科学的および工学的問題を分析および解決するためのコンピューターの使用として、「科学情報学」という用語の意味を理解しています。 単純な数値計算と区別します。 教育における科学情報学の使用は、生徒と教師の両方にとって常に難しい課題です。 このような学習プロセスは、多くの技術的および学際的な問題を扱い、数学的知識とコンピューターサイエンスの同期も必要とします。 これらの困難を克服するために、指導に対する構成主義的アプローチに基づいており、教師に適切な構造的基盤を提供する一連の指導原則と方法論を提供します。 これにより、学生はコンピュータモデルを使用して一連の計算実験を行うことができます。 このアプローチは数学とプログラミングの知識に関連しており、これらはメイントレーニングコースの過程で教えられ、密接に関連しています。 計算統計のセクションは、科学情報学の入門セクションであり、この研究の応用分野として考えられます。 この方法論の背景を以下に示します。

1.1。 科学情報学

KarniadaxとKirby IIは、「コンピューターインフォマティクスを模倣研究の核心」と定義しました。 著者は、「数値アルゴリズム、最新のプログラミング手法、並列計算への全体的なアプローチを提案します。多くの場合、こうした概念や類似のツールはさまざまな関連トピック、コース、教科書で定期的に研究され、それらの関係はすぐに明らかになります。 コンセプトとツールを統合する必要性は、通常、コースを修了した後、たとえば最初の大学院での作業中、または論文の要約を書くときに明らかになり、それにより、学生は3つの独立した分野の理解を1つにまとめて、望ましい解決策を得ることができます。 このプロセスは間違いなく非常に価値がありますが、多くの時間を要し、多くの場合、概念とツールの効果的な組み合わせを提供しない場合があります。 教育学の観点から、科学情報学のトピックの理解を深めるために、総合的な統合アプローチは、学生を一度にいくつかの分野に刺激することができます。 図1は、数値数学、情報学、モデリングの共通部分としての科学情報学の定義を示しています[16]。







図 1.科学情報学。

1.2。 学習における構成主義

ケインとケインの基礎研究[6]では、学習における構成主義の基本原則を提案しました。 私たちにとって最も重要なことの1つは、「脳が部分と全体を同時に処理すること」です。



このように、よく組織された学習プロセスは、基礎となる詳細とアイデアを実証します。 モデリングベースのアプローチを使用すると、シミュレーションモデルを作成した後、調査の目的が明らかになります。 これにより、結果を観察し、関連する結論を立てることができます。

1.3。 モデリングベースの学習：なぜモデルなのか？

ギボンズは、2001年にシミュレーションベースのトレーニングプログラムを導入しています[9]。 次の基本原則を強調します。

• 生徒はモデルとのやり取りを通じて経験を積む。
• 学生はモデルを実験することで科学的および工学的な問題を解決します。
• 問題の検討と声明;
• 特定の教育目標の定義;
• 決定の文脈におけるすべての必要な情報の提示。

Millard et al。[30]は、「インタラクティブモデリング」を使用した学習促進モデルを提案しています。 著者は、「システムダイナミクス」に基づく「有望な方法論」に基づく現代のコンピューターテクノロジーを紹介します。 「実際の経験には、インタラクティブなモデルの構築、およびそれらを使用した仮説と実験のテストが含まれます。」



Lehrer and Schauble [25]は、モデルのさまざまな表現を使用した実験に焦点を当てています。「学生がモデルのいくつかのバージョンを作成および修正し、これらのさまざまなモデルの記述の妥当性を比較する機会があると、学生の学習が強化されます。」

1.4。 教育の中心にある科学情報学：モデルを使った実験

Xue [40]は、「科学情報学」に基づいた教育の改革を、モデリングと模倣を通じて提案しています。 彼は「...モデリングとシミュレーションを使用して、プログラミング、モデリング、データ分析の現在の問題を解決する...」とアドバイスしています。 モデリングベースの学習は数学教育で使用されます。 Geogebraソフトウェアを使用して多くのモデルが構築されました[33]。 モデルは科学教育で主要な役割を果たします[7,18]。

1.5。 キューイングシステムの確率的モデリング

初期定義の単純さと、モデリングとシミュレーションの幅広い可能性のために、キューイングシステムの使用を提案します。 マスサービス理論はよく知られており、マスサービスシステム（QS）のシミュレーションは、科学[4.19]および教育[13.36]で広く使用されています。 マルチフェーズキューイングシステムは、並列コンピューティングの使用と同様に、学生の実験に適したプラットフォームです。 また、研究と研究には多くの興味深い理論的結果があります[12]。

1.6。 科学情報学教育におけるPython

Pythonは、科学者や教育者にとって最も人気のあるプログラミング言語の1つです[21–23]。 Pythonは産業科学計算で広く使用されています[14]。 Langtangenは、オスロ大学で科学情報学を教えるための主要言語としてPythonを使用した彼の長期的な経験について報告しています[24]。 Pythonはプログラミングを研究する最初の言語[38]として、また計算手法の詳細な研究[3,20,34]として進歩しています。

2.基本

モデリングを開始する前に、プロセスで使用する主要なアプローチを定義します。 この章では、乱数生成と確率分布、確率的モデリングの問題に取り組みます。 初等確率論を考えてみましょう。 これらの実験の主な目的は、中心極限定理の実験的証明です。 モデルとこれらのモデルを使用した実験により、擬似乱数ジェネレーターと準乱数ジェネレーターの原理が明確になり、指数分布が理解されます。 これは、QSモデルを使用したより詳細な実験の基礎を提供します。

2.1。 ランダム変数と分布

確率論のすべての要素は伝統的に理解するのが難しいと考えられており、常に国際教育機関の利益の範囲内にあります[15]。 同時に、これらの問題は科学研究において重要な役割を占めています[10]。 モデリングベースのアプローチにより、この資料の理解が容易になります。 この記事で取り上げるモデルは、1つから複数のサイコロを投げるための単純なモデルです。



これらの導入実験のタスクは非常に複雑です。 確率分布だけでなく、モデリングと並列計算も取り上げます。 また、科学研究の一歩を踏み出します。中央極限定理を実験的に証明します。



（分布に影響を与えることなく）乱数を生成することから始めます。 次に、一様分布のランダム変数について説明します。 真のランダム性と準ランダム性に関する議論は、著者によって提示されています[26、35]。 上級者向けに、Python疑似ランダム変数ジェネレーターを使用した一連の実験が紹介されます。 初期段階では、研究を明確にするために、シミュレーション結果を観察しながらテストの数を増やします。 次の段階では、より複雑な実験と並列計算に進みます。 モデリングにはPythonのランダム変数モジュールを使用し、並列計算にはmpi4pyライブラリを使用します。 Pythonランダム変数モジュールは、さまざまな分布の擬似乱数ジェネレーターに基づいています。 例： random.randint（a、b）は、ランダムな整数Nを返します。ここで、 a≤N≤bおよびrandom.expovariate（lambd）は、パラメーター 'lambd'を使用して指数分布したランダム変数を返します。 詳細については、Pythonのドキュメントを参照してください。 立方体投げモデルのプログラミングを図2に示します。

import pylab import random number_of_trials =100 ## Here we simulate the repeated throwing of a single six-sided die list_of_values = [] for i in range(number_of_trials): list_of_values.append(random.randint( 1,6)) print "Trials =", number_of_trials, "times." print "Mean =", pylab.mean(list_of_values) print "Standard deviation =", pylab.std(list_of_values) pylab.hist(list_of_values, bins=[0.5,1.5,2.5,3-5,4.5,5.5,6.5]) pylab.xlabel('Value') pylab.ylabel('Number of times') pylab.show()
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

図 2. Pythonで単一のダイスを投げるモデルのプログラミング



1つのダイをトスしたシミュレーションの結果を図3に示します。









図 3. 1つのダイスのトスをモデリングした結果



次に、2つのサイコロを投げる場合を考えます。 この段階での主なアイデアは、異なる数のキューブを使用した実験を使用した中央処理センターの説明です。 図4はこの考え方を示しています。









図 4.確率密度関数の比較



調査プロセスは、コードを修正して、複数のサイコロのケースを検討し始めるような方法で2つのサイコロを投げることをシミュレートすることによって続行されます。 コードは、以下に示す2行のコードを除いて、1つのキューブを持つコードに似ています。

 ... list_of_values.append(random.randint(1, 6) + random.randint(1, 6)) ... pylab.hist(list_of_values, pylab.arange(1.5, 13.5, 1.0)) ...
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

2つのキューブの場合の計算結果を図5に示します。









図 5. 2つのキューブの場合



これで、正規分布を検討できます。 この段階でのタスクは、いくつかのキューブを持つ前のケースがどのように正規分布と相関するかを示すことです。 次のタスクでは、平均と標準偏差を紹介します。 コードは、以下の手順を除き、単一のキューブの場合と同じままです。

 ... list_of_values.append(random.normalvariate(7, 2.4)) ...
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

正規分布のシミュレーション結果を図6に示します。









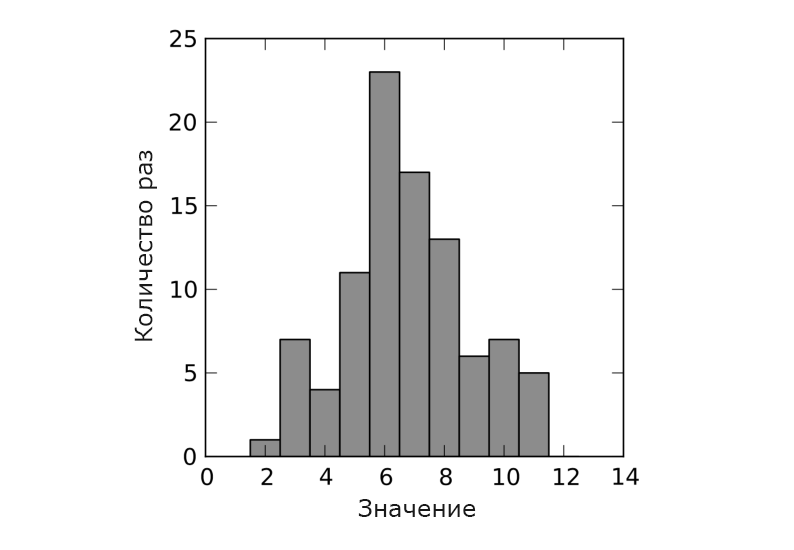
図 6.正規分布のシミュレーション結果



最後のステップは、指数分布を示すことです。 指数分布は、さまざまなタイプのシステムで要件を受信した瞬間の間隔の分布（期間）をモデル化するために使用されます。 それらのモデリングの結果は、図7および8に示されています。

 import pylab import random number_of_trials = 1000 number_of_customer_per_hour = 10 ## Here we simulate the interarrival time of the customers list_of_values = [] for i in range(number of trials): list_of_values.append(random.expovariate(number_of_customer_per_hour)) mean=pylab.mean(list_of_values) std=pylab.std(list_of_values) print "Trials =", number_of_trials, "times" print "Mean =", mean print "Standard deviation =", std pylab.hist(list_of_values,20) pylab.xlabel('Value') pylab.ylabel('Number of times') pylab.show()
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

図 7.指数分布のPythonモデル









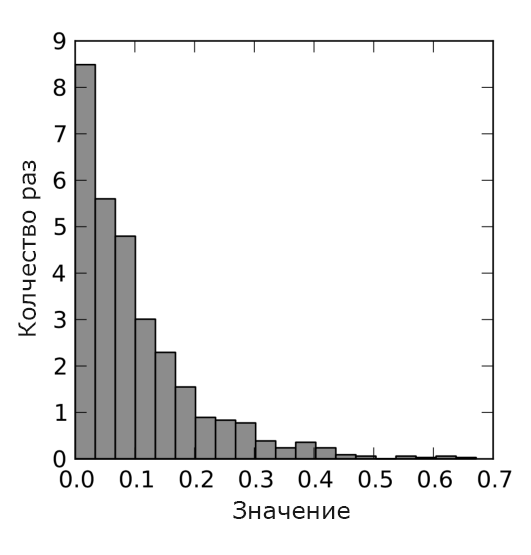
図 8.指数分布のシミュレーション結果

2.2。 確率的モデリング

確率的モデリングは科学情報学の重要な要素です。 モンテカルロ法に焦点を当てます[10,11,27]。 モデルが構築された後、ランダム変数を生成し、システムのさまざまなパラメーターを実験できます。 この記事では、モンテカルロ実験の重要なポイントは、結果を蓄積して統合するためにテストを何度も繰り返すことです。 最も簡単なアプリケーションについては、前のセクションで説明しました。 テストの数を増やすことにより、シミュレーション結果の精度が向上します。



ここで、学生はテストの数を増やすことにより、この単純なモデルを使用して特定の数の実験を行う必要があります。 キューブの数とテストの数が増えるため、生徒は比較的長い計算時間に直面します。 これは、並列コンピューティングを使用する大きな理由です。 いくつかのサイコロのPythonモデルを図9に示します。シミュレーション結果を図10に示します。次のステップでは、さまざまなキューシステムに関連するより一般的な問題を検討します。 QS分類の概要については、この記事の次のパートで説明します。 M / M / 1システムとより複雑なキューイングシステムで調査を開始します。 確率的プロセスの基本概念については、この記事のこの部分で詳しく説明します。 可能な例として、出力ストリームを調べる問題を提案できます。 M / M / 1システムの導出がポアソンフローであることを証明しましょう。 したがって、収集されたデータは、構築された経験的ヒストグラムの形式で表示されます。

 import pylab import random number_of_trials = 150000 number_of_dice = 200 ## Here we simulate the repeated throwing ## of a number of single six-sided dice list_of_values = [] for i in range(number_of_trials): sum=0 for j in range(number_of_dice): sum+=random.randint(1,6) list_of_values.append(sum) mean=pylab.mean(list_of_values) std=pylab.std(list_of_values) print "Trials =", number_of_trials, "times" print "Mean =", mean print "Standard deviation =", std pylab.hist(list_of_values,20) pylab.xlabel('Value') pylab.ylabel('Number of times') pylab.show()
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

図 9.拡張正規分布のPythonモデリングモデル









図 10.拡張正規分布のシミュレーション結果

3.多相待ち行列システムと確率的モデリング

以下は、モデリングと確率論のニュアンスを考慮に入れた、QSの入門説明です。

3.1。 バルクサービスシステム

単純なキューイングシステムは、着信要求を処理する1つのサービングデバイスで構成されます。 単純なキューイングシステムの一般的なスキームを図11に示します。一般に、QSは着信要求を処理する1つ以上のサービス提供デバイスで構成されます。 各フェーズで1つ以上のサービスデバイスを使用する1つ以上のサービスステージも可能です。 すべてのサーバーがビジーであるとわかる着信クライアントは、サービスを提供するデバイスの前にある1つ以上のキューに参加しています。 実動システム、通信システム、保守システムなど、QSをシミュレートできる多くのアプリケーションがあります。 一般的なQSは、アプリケーションのフロー、サービスプロセス、キューサービスメソッドの3つの主要なコンポーネントで特徴付けられます。 アプリケーションは、いくつかの限定されたソースまたは無制限のソースから提供されます。









図 11.シンプルQS。



アプリケーションプロセスでは、アプリケーションがシステムに入る方法を説明します。 定義する

$$$\ alpha_i$ アプリケーションの到着間の時間間隔として $$$（i -1）$ そして $$$i$ アプリケーション、アプリケーションの受信間の予想（平均）時間 $$$E（\アルファ）$ およびアプリケーションの受信頻度 $$$\ lambda = \ frac {1} {E（\ alpha）}$



私たちも定義します $$$s$ 提供デバイスの数として。 サービスメカニズムはこの番号によって決定されます。 各サービングデバイスには独自のキューがあり、アプリケーションのサービス時間の確率的分布もあります。



定義する $$$s_i$ サービスは何時ですか $$$i$ 番目のアプリケーション $$$E（s）$ アプリケーションの平均サービス時間として $$$\ mu = \ frac {1} {E（s）}$ アプリケーションのサービス速度として。



サービスデバイスがキューから次のチケットを選択するために使用するルールは、QSキューディシプリンと呼ばれます。 最も一般的なキューの分野は次のとおりです。優先度—顧客は重要度の高い順にサービスされます。 FIFO-先着順; LIFOがスタックで、最後のものが最初に提供されました。 拡張Kendallシステム分類は6文字を使用します：A / B / s / q / c / p、ここでAは着信要求間の間隔の分布、Bはサービス間隔の分布、sはサーバー数、qはサービス規律（FIFOでは省略） 、-システム容量（無限キューでは省略）、p-可能なリクエストの数（オープンシステムでは省略）[17.37]。 たとえば、M / M / 1は、ポアソン入力ストリーム、1つの指数サービングデバイス、1つの無限FIFOキュー、および無限数のアプリケーションを表します。



QSは、科学技術のさまざまな分野のモデリングと研究に使用されます。 たとえば、キュ​​ーイング理論を使用して、生産システムまたは輸送システムをモデリングおよび研究できます。 さらに、サービス要求はアプリケーションと見なされ、保守手順はサービスメカニズムと見なされます。 次の例はこれです：コンピューター（それぞれ端末要求とサーバー応答）、コンピューターマルチディスクメモリシステム（データの書き込み/読み取り要求、共有ディスクコントローラー）、トランク無線通信（電話信号、リピーター）、コンピューターネットワーク（要求、チャネル）[39 ]。 生物学では、キューイング理論を使用して、酵素システム（タンパク質、一般酵素）をモデル化できます。 生化学では、キューイングネットワークモデルを使用して、LACオペロンの調節回路を研究できます。

3.2。 なぜ多相なのか？

直列に接続され、無制限の数のアプリケーションを持つ複数のサービスデバイスで構成されるマルチフェーズQSを検討します。 リクエスト間の時間と処理時間は独立しており、指数関数的に分散しています。 ラインナップは、FIFOサービスの分野では無限です。 マルチフェーズQSは、当然、マルチコアコンピューターシステムのトポロジを反映しています。 後で見るように、各モデルはプログラミング言語で簡単に記述し、調査および修正できます。 このモデルは、さまざまなマルチプロセッシングアプローチの比較研究も可能にします。 マルチフェーズQSモデルを図12に示します。









図 12.マルチフェーズQS。

3.3。 理論的根拠

統計モデリングの場合、コンピューターコードを検証するという問題に常に直面しています。 プログラムまたはアルゴリズムのエラーの問題は常に未解決のままです。 モデルは完全に分析的ではなく、プログラムを実行するたびに、入力/出力に異なるデータがあります。 したがって、コードまたはアルゴリズムの正確性を確認するには、さまざまなアプローチが必要です（完全に確定的な入力データの場合に使用するアプローチから）。 この問題を解決するには、科学文献に記載されているいくつかの研究の理論的結果を適用する必要があります。 これらの結果は、出力データの検証と分析、およびシミュレーション結果の正確さの問題を解決するための基礎となります[31,32]。



マルチフェーズQSでのアプリケーションの滞留時間を調査します。 示す $$$T_j、_n$ システム内のアプリケーションが費やした時間として、 $$$S_n ^ {（j）}$ j番目のフェーズのn番目のアプリケーションのサービス時間として。 検討する $$$\ alpha_k$ どうやって $$$E（\アルファ）$ k番目のフェーズ。



そのような定数があります $$$\ gamma> 0$ そのような

$$

$$$ sup_ {n \ geq2} E | S_n ^ {（j）} | ^ {4+ \ gamma} <\ infty、j = 0、1、2、...、k \;（1）\\ \ alpha_k> a_ {k-1}> ...> \ alpha_1> 0 \;（2）$$

定理 条件（1）および（2）が満たされる場合、

$$

$$P \ bigg（\ overline \ lim_ {n \ to \ infty} \ frac {T_ {j、n}-\ alpha_j \ cdot n} {\ widetilde {\ sigma} \ cdot \ alpha（n）} = 1 \ bigg）= \\ P \ bigg（\下線\ lim_ {n \ to \ infty} \ frac {T_ {j、n}-\ alpha_j \ cdot n} {\ widetilde {\ sigma} \ cdot \ alpha（n） } = -1 \ bigg）= 1、\\ j = 1、2、...、3、k \; ; \ alpha（n）= \ sqrt（2n \ ln \ ln n）$$

3.4。 統計モデリング

モデルが構築された後、このモデルで一連の実験を行うことができます。 これにより、システムの特性の一部を調べることができます。 予想される平均値でランダムな値を生成し、調査に必要な値を計算します（以下に示す再帰方程式を使用）。 これらの値もランダムになります（モデルの入力データの確率論-アプリケーションの到着とランダムなサービス時間の間のランダムな時間）。 その結果、これらのランダム変数（変数）のパラメーター（平均値と確率分布）を計算できます。 この方法は、モデルにランダム性が存在するため、統計モデリングと呼ばれます。 より正確な結果が必要な場合は、モデルで実験を繰り返してから結果を統合し、積分特性（平均値または標準偏差）を計算する必要があります。 これはモンテカルロ法と呼ばれ、記事でもう少し詳しく説明されています。

3.5。 再帰方程式

前述のQSのモデリングアルゴリズムを開発するには、いくつかの数学的な構造を分析する必要があります。 主なタスクは、マルチフェーズQSでの番号nのアプリケーションの滞留時間を調べて計算することです。 $$$k$ フェーズ。 次の再帰方程式[12]を与えることができます。 $$$t_n$ -到着時間 $$$n$ 番目のアプリケーション。 $$$S_n ^ {（j）}$ サービス時間はどうですか $$$n$ 申込み $$$j$ 段階 $$$\ alpha_n = t_n-t_ {n-1}; j = 1、2、...、k; n = 1、2、...、N.$ 。 次の繰り返し方程式は、待ち時間について成り立ちます $$$T_ {j、n}$ のために $$$n$ 申込み $$$j$ フェーズ：

$$

$$T_ {j、n} = T_ {j-1、n} + S ^ {j} _n + \ max（T_ {j、n-1}-T_ {j-1、n}-\ alpha_n、0） ; \\ \\ j = 1、2、...、k; n = 1、2、...、N; \\ \\ T_ {j、0} = 0、\ forall j; T_ {0、n} = 0、\ forall n;$$

推測する マルチフェーズQSでのアプリケーションの滞留時間を計算するための繰り返し方程式。



証明。 時間があれば $$$\ alpha_n + T_ {j-1、n}≥T_ {j、n-1}$ 、その後の待ち時間 $$$j$ 段階 $$$n$ thアプリケーションは0です。この場合 $$$\ alpha_n + T_ {j-1、n} <T_ {j、n-1}$ での待ち時間 $$$j$ 段階 $$$n$ 申込み $$$\ omega_j ^ n = T_ {j、n-1}-T_ {j-1、n}-\ alpha_n$ そして $$$T_ {j、n} = T_ {j-1、n}-\ omega_j ^ n + S_n ^ {（j）}$ 。 上記の2つのケースを考えると、予想される結果になります。



これで、得られたすべての理論結果に基づいて必要なアルゴリズムの実装を開始できます。

4.マルチプロセッシング用のPython

プログラミング言語としてのPythonは、科学者や教育者の間で非常に人気があり、科学指向の問題を解決するのに非常に魅力的です[3]。 Pythonは、グラフィカルユーティリティ、幅広い数学的および統計パッケージ、およびマルチプロセッシング用パッケージを含む、モデリングとシミュレーションのための強力なプラットフォームを提供します。 実行時間を短縮するには、PythonコードとCコードを組み合わせる必要があります。 これらすべてが、統計データと処理結果を取得するための強力なモデリングプラットフォームを提供します。 モデリングでも重要なPythonの重要な概念は、デコレータ、コルーチン、yield式、マルチプロセッシング、およびキューです。 ビーズリーは本の中でこれらの点を非常によく調べていた[2]。 それにも関わらず、プロセス間通信を整理する方法はいくつかあり、キューの使用から始めます。これは、QSの研究の観点から非常に自然なことです。



以下は、マルチプロセッシングを使用してプログラムコードの効率と有効性を高める利点の簡単な例です。 学生は、スーパーコンピューターまたはクラスターシステムで並列計算を使用することにより、シミュレーション結果を改善できます[28、29]。 一方で、マルチプロセッシングを使用すると、マルチフェーズモデルをマルチコアプロセッサのリソースと比較できます。他方では、マルチプロセッシングを使用して一連の並列モンテカルロテストを実行できます。 次のセクションでは、これら2つのアプローチを検討します。 やる気のある学生のために、Pythonを使用したマルチプロセッシングの簡単な紹介を以下に示します。



まず、mpi4pyモジュールを使用します。 これは、MPIがどのように機能するかの主要なアイデアを提示するために重要です。 提供されたプログラムをユーザー定義のプロセッサコアの1つにコピーし、gather（）メソッドを使用した後に結果を統合します。 Pythonコードの例（図13）とシミュレーション結果（図14）を以下に示します。

 #!/usr/bin/python import pylab import random import numpy as np from mpi4py import MPI dice=200 trials= 150000 rank = MPI.COMM_WORLD.Get_rank() size = MPI.COMM WORLD.Get_size() name = MPI.Get_processor_name() random.seed(rank) ## Each process - one throwing of a number of six-sided dice values= np.zeros(trials) for i in range(trials): sum=0 for j in range(dice): sum+=random.randint(l,6) values[i]=sum data=np.array(MPI.COMM_WORLD.gather(values, root=0)) if rank == 0: data=data.flatten() mean=pylab.mean(data) std=pylab.std(data) print "Number of trials =", size*trials, "times." print "Mean =", mean print "Standard deviation =", std pylab.hist(data,20) pylab.xlabel('Value') pylab.ylabel('Number of times') pylab.savefig('multi_dice_mpi.png')
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

図 13. MPIを使用した拡張正規分布のPythonモデル。









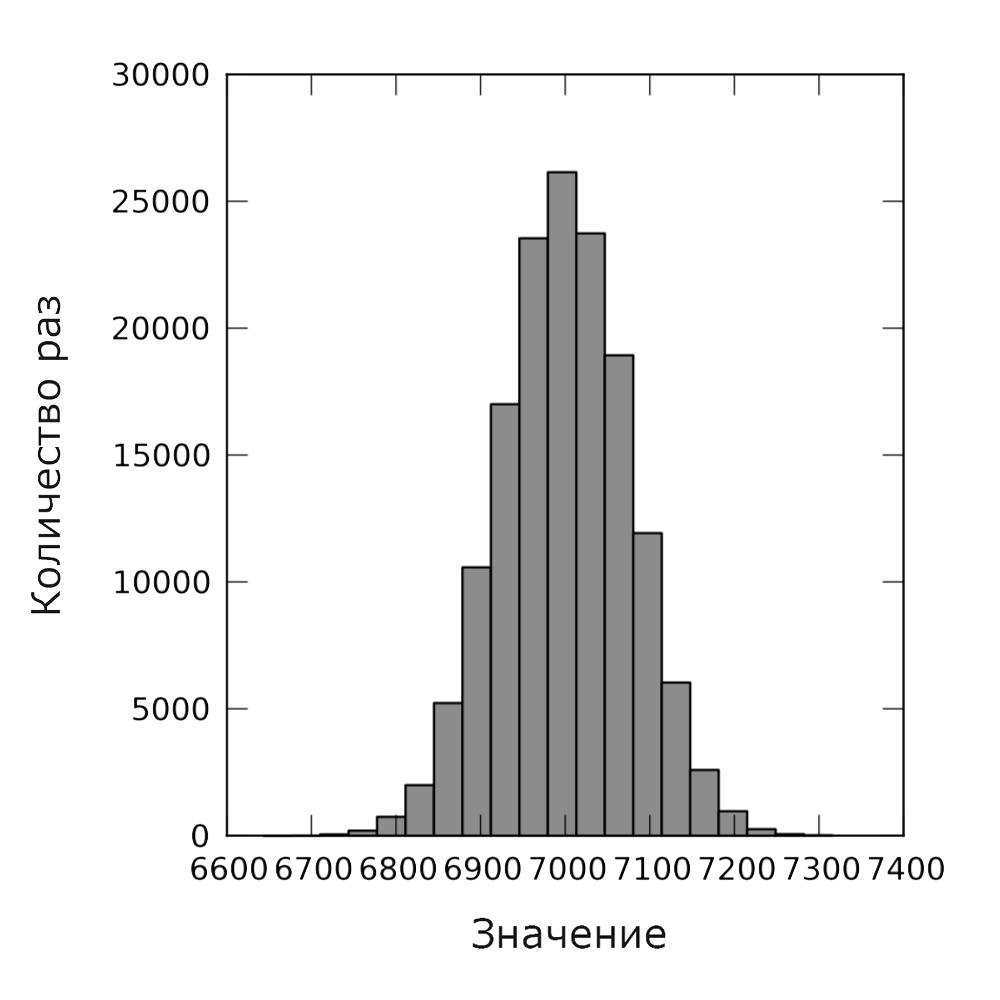
図 14. MPIを使用した正規分布。

5.モデリングベースの教育アプローチ

マルチフェーズQSは、適切なシミュレーションベースのアプローチを開発するためのコアを提供します。 このアプローチには、前のセクションで説明した基本的な概念と、より複雑な理論的な結果と方法が含まれます。 主なアイデアは、本質的に確率論的です：ランダム変数、ランダムな数値分布、乱数ジェネレーター、中央極限定理。 Pythonプログラミング構成：

デコレータ、コルーチン、およびyeild式。 より複雑な結果には、システムでのアプリケーションの滞留時間、QSでのアプリケーションの滞留時間を計算するための回帰方程式、確率的モデリング手法、マルチプロセッサテクノロジーなどの理論的概念が含まれます。 図15は、学歴を説明する主な概要を示しています。









図 15.モデリングベースの教育アプローチ



これらすべての理論的およびプログラム的構造により、学生は多相QSのさまざまなモデルで実験を行うことができます。 このような実験の目的は2つあります。 第一に、これにより、学生は次のシーケンスを理解することができます。これは、あらゆる科学研究で重要です：理論的事実、数学モデル、ソフトウェア構成、コンピューターモデル、確率モデル、および学習に必要なシミュレーション結果の観察。 これにより、学生は一般的な研究の全体像を得ることができます（図16）。









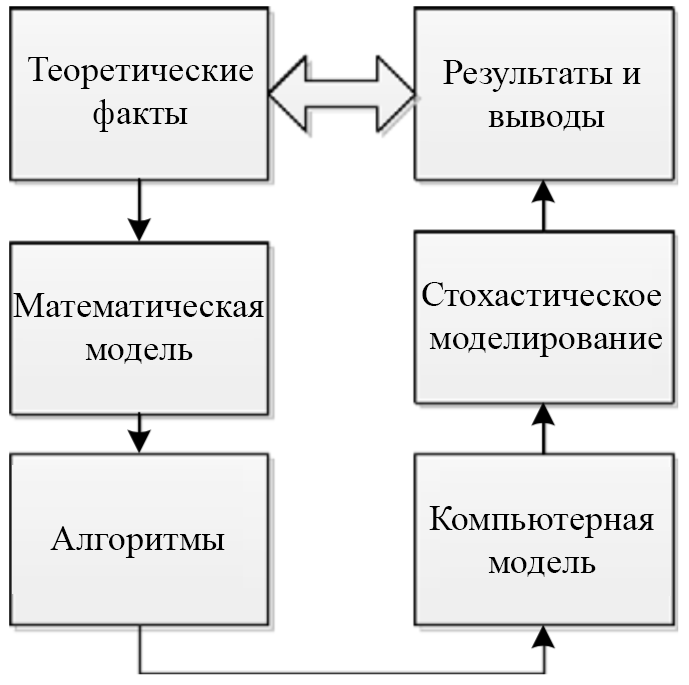
図 16.研究分野



このようなアプローチは、確率的モデリングと、マルチプロセッシングや並列プログラミングなどの基本的なソフトウェア構成のより深い理解を提供します。 これらの規定は、科学計算の分野で最も重要です。

5.1。 モデル実験

このセクションでは、マルチフェーズQSの3つのコンピューターモデルについて検討します。 これらのモデルはすべて、哲学的および主要な機能が異なります。 実験の目的は統計モデルを作成し、多相システムの主なパラメーターを研究することであるという事実にもかかわらず、これらのモデルの概念的な考え方は完全に異なっています。 これらの基本的な考え方を比較することで、学生は並列計算、マルチプロセッサ統計、シミュレーションモデリングの基礎となる基本原則を理解するのに役立ちます。



最初に紹介したモデルはリアルタイムの記録に基づいており、シミュレーションモデルと呼ばれます。 Pythonマルチプロセッサモジュールを使用します。このモデルの精度は、time（）メソッドの精度と解像度に依存します。さまざまな汎用オペレーティングシステムの場合は非常に低く、リアルタイムシステムの場合は非常に高くなります。学生は、以前に提案された反復方程式を使用してこのモデルを変更し（システムでのアプリケーションの滞留時間を計算するため）、両方のケースで結果を比較できます。



次のモデルは、システム内のアプリケーションの滞留時間を計算し、確率的モデリングに基づいています。モデルはマルチプロセッサを直接使用しません。マルチプロセッシングは、Pythonのyield式を使用してエミュレートされます。



Python MPI mpi4pyモジュールを使用して、最新モデルがここに表示されます。ここでは、統計モデリングに実際のMPI（マルチプロセッサ）アプローチを使用します。これにより、モンテカルロ法のテスト数を増やすことができます。



一般に、学生の課題は、提供されたモデルを使用して一連の実験を作成し、マルチフェーズQSでのアプリケーションの滞留時間に対する反復対数の法則の実験的証拠を取得することです。

5.2。 マルチプロセッササービスを使用したシミュレーションモデル

以下はシミュレーションモデルです。検討すべき主な問題は、シミュレーションモデルと統計モデルの違いです。もう1つの重要な問題は、シミュレーションモデルの正確さと精度です。また、提示されたモデルの正確さと精度の問題も重要です。学生は、処理の間隔や頻度、アプリケーションの数、サービングノードの数などのさまざまなパラメーターに応じて、シミュレーション結果を調べて比較できます。モデルの一般的なスキームを図17に示します。









図 17.シミュレーションモデル



プログラムコードコードは2つの主要部分で構成されています。前者は計算を直接目的とし、次は結果を構築するためのものです。計算用のモジュールには、3つの主要な機能が含まれています。producer（）-アプリケーションを受け取り、そもそも配置するためのもの。サーバー（）-アプリケーションのサービス用。 consumer（）-結果を取得します。このソフトウェアモデルは実際のシミュレーションに基づいており、計算に数式を使用しません。その精度は、Python一時モジュールの精度に依存し、原則として、オペレーティングシステムに依存します。サービングデバイスの動作の計算は、マルチプロセッサシステム内のさまざまなプロセス間で分散されます。上記のモデルを実装するためのコンピューターコードを図18に示します。

 import multiprocessing import time import random import numpy as np def server(input_q,next_q,i): while True: item = input_q.get() if i==0:item.st=time.time() ## start recording time ## (first phase) timc.sleep(random.expovariate(glambda|i])) ##stop recording time (last phase) if i==M-1 :item.st=time.time()-item.st next_q.put(item) input_q.task_done() print("Server%d stop" % i) ##will be never printed why? def producer(sequence,output_q): for item in sequence: time.sleep(random.expovariate(glambda[0])) output_q.put(ilem) def consumer(input_q): "Finalizing procedures" ## start recording processing time ptime=time.time() in_seq=[] while True: item = input_q.get() in_scq+=[item] input_q.task_done() if item.cid == N-1: break print_results(in_seq) print("END") print("Processing time sec. %d" %(time.time()-ptime)) ## stop recording processing time printf("CPU used %d" %(multiprocessing.cpu_count())) def print_resulls(in_seq): "Output rezults" f=open("out.txt","w") f.write("%d\n" % N) for l in range(M): f.write("%d%s" % (glambda[t],",")) f.write("%d\n" % glambda[M]) for t in range(N-1): f.write("%f%s" % (in_seq[t].st,",")) f.write("%f\n" % (in_seq[N-1].st)) f.close() class Client(object): "Class client" def __init__(self,cid,st): self.cid=cid ## customer id self.st=st ## sojourn time of the customer ###GLOBALS N=100 ## total number of customers arrived M=5 ## number of servers ### glambda - arrival + servicing frequency ### = customers/per time unit glambda=np.array([30000]+[i for i in np.linspace(25000,5000,M)]) ###START if __name__ == "__main__": all_clients=[Client(num,0) for num in range(0,N)] q=[multiprocessing.JoinableQueue() for i in range(M+1)] for i in range(M): serv = multiprocessing.Process(target=server,args=(q[i],q[i+1],i)) serv.daemon=True serv.start() cons = multiprocessing.Process(target=consumer,args=(q[M],)) cons.start() ### start 'produsing' customers producer(all_clients,q[0]) for i in q: i.join()
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

図 18.マルチプロセッササービスを使用したシミュレーションモデルのPythonコード。



勉強する質問：

• グローバル変数はプロセスにどのように提供され、プロセス間で共有されますか？
• さまざまなサービスデバイスに関連付けられたプロセスを完了する方法
• 異なるプロセス間で情報フローはどのように送信されますか？
• モデルの正確さはどうですか？
• モデルの有効性はどうですか。異なるプロセス間で情報を交換するのにどれくらい時間がかかりますか？

これで、matplotlibモジュールを使用して結果を印刷し、チャートを表示した後、結果を視覚的に分析できます。モデルをさらに改善する必要があることがわかります（図19）。したがって、より強力なモデルに進むことができます。









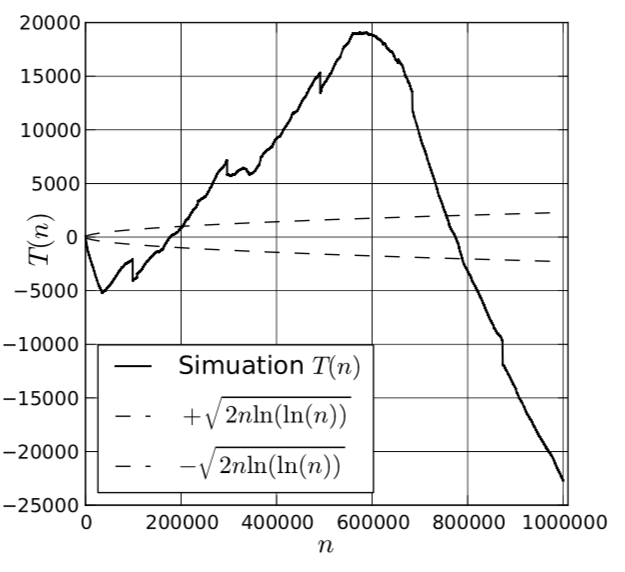
図 19.マルチプロセッササービスのシミュレーションモデルをモデル化した結果。

5.3。 統計モデル単位プロセス

統計モデルの主な特徴は次のとおりです。現在、再帰方程式を使用して、システム内のアプリケーションの滞留時間を正確に計算します。特定のPythonコルーチン関数を使用して、すべてのデータを単一のプロセスで処理します。計算の信頼性を最大限に高めるために、一定数のモンテカルロシミュレーションを実行します。このモデルにより、システム内のアプリケーションの滞留時間を「正確に」計算できます。モデルの主な概要を図20に示します。学生は、シミュレーションモデルと統計モデルの違いを調べることができます。









図 20.統計モデルの単一プロセス：



上記のモデルを実装するためのプログラムコードを図21に示します。シミュレーション結果を図22に示します。

 #!/usr/bin/python import random import time import numpy as np from numpy import linspace def coroutine(func): del start(*args,**kwargs): g = func(*args,**kwargs) g.next() return g return start def print_header(): "Output rezults - header" f=open("out.txt","w") f.write("%d\n" % N) ##number of points in printing template f.write("%d\n" % TMPN) for t in range(M): f.write("%d%s" % (glambda[t],",")) f.write("%d\n" % glambda[M]) f.close() def print_results(in_seq): "Output rezults" f=open("out.txt","a") k=() for i in range(N-2): if in_seq[i].cid==template[k]: f.write("%f%s" % (in_seq[i].st,",")) k+=1 f.write("%f\n" % (in_seq[N-1 ].st)) f.close() coroutine def server(i): ST=0 ##sojourn time for the previous client item=None while True: item = (yield item) ##get item if item == None: ##new Monte Carlo iteration ST=0 continue waiting_time=max(0.0,ST-item.st-item.tau) item.st+=random.expovariate(glambda[i+1])+waiting_time ST=item.st def producer(): results=[] i=0 while True: if i == N: break c=Client(i,0.,0.) if i!=0: c.tau=random.expovariate(glambda[0]) i+= 1 for s in p: c=s.send(c) results+=[c] for s in p: c=s.send(None) ##final signal return results class Client(object): def __init__(self,cid,st,tau): self.cid=cid self.st=st self.tau=tau def params(self): return (self.cid,self.st,self.tau) stt=time.time() N=1000000 ## Clients M=5 ## Servers ## Input/sevice frequency glambda= [30000]+[i for i in linspace(25000,5000,M)] MKS=20 ## Monte Carlo simulation results ## Number of points in the printing template TMPN=N/10000 ##printing template template= map(int,linspace(0,N-1,TMPN)) print_header() p=[] for i in range(M):p +=[server(i)] for i in range! MKS): print_results(producer()) print("Step=%d" % i) sys.stdout.write("Processing time:%d\n" % int(time.time()-stt))
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

図 21.単一プロセス統計モデルのPythonコード









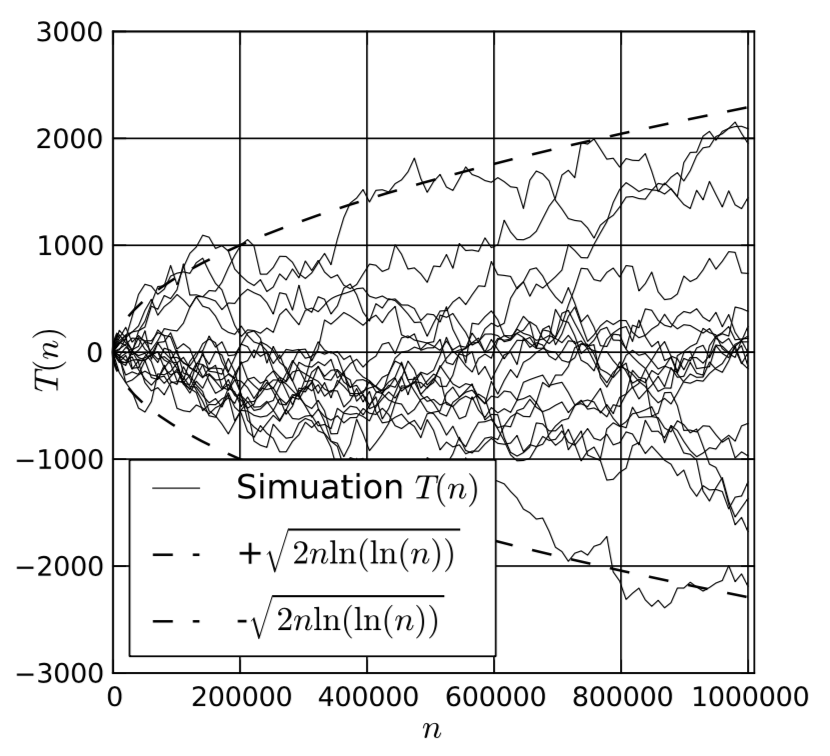
図 22.統計モデルの単一プロセスのシミュレーション結果

5.4。 MPIの統計モデル

モデル開発の次のステップは、Python MPIモジュール-mpi4pyの使用です。これにより、多数のモンテカルロシミュレーションで作業し、クラスターを使用してモデルを実行およびテストできます。次のステップは、Python用のCプログラミング言語、「実際の」MPIまたはSWIG（https://ru.wikipedia.org/wiki/SWIG）テクノロジーの使用に基づいて、モデルをさらに改善することです。このモデルは以前のモデルとほとんど同じですが、mpi4pyがマルチプロセッシングと結果の統合に使用される点が異なります（図23）。









図 23.統計MPIモデル



前のモデルに加えて、いくつかの追加モジュールをインポートする必要があります。この段階でさらにテストを行うため、print_results（）関数も書き換える必要があります。また、プログラムの主要部分を書き換える必要があります。図24では、以前のモデルのコードとは異なるプログラムコードの部分のみを提供しています。シミュレーション結果を図25に示します。

 .................... import sys from mpi4py import MPI .................... def print_results(in_seq): "Output rezults" f=open("out.txt","a") for m in range(int(size)): for j in range(MKS): for i in range(TMPN-l): f.write("%f%s" % (in_seq[m][i+j*TMPN].st,",")) f.write("%f\n" % (in_seq[m][(TMPN-l)+j*TMPN].st)) f.close() .................... stt=time.time() #start time for the process rank = MPI.COMM_WORLD.Get_rank() size = MPI.COMM_WORLD.Get_size() name = MPI.Get_processor_name() N= 10**3 ## Clients M=5 ## Servers ## Input/sevice frequency glambda=[30000]+[i for i in linspace(25000,5000,M)] ## Number of Monte-Carlo simulations for this particuar process MKS=20 TMPN=200 ## Number of points in printing templat template= map(int,linspace(0,N-1,TMPN)) ## points for printing p=[] results=[] ## this process results total_results=[] ## overall results for i in range(M):p +=[server(i)] for i in range(MKS):results+=producer() total_results=MPI.COMM_WORLD.gather(results,0) random.seed(rank) if rank == 0: print_header() print_results(total_results) sys.stdout.write("Processing time: %d\n" % int(time.time()-stt))
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

図 24. MPIベースの統計モデルのPythonコード









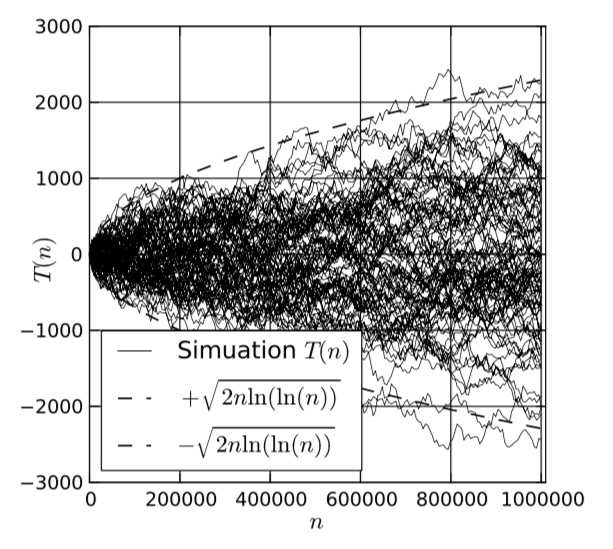
図 25.統計モデルMPIのシミュレーション結果

6.結論

この記事では、シミュレーションベースの学習のためのいくつかのモデルを調べました。これらのモデルにより、学生は一連の実験を実施し、科学情報学の分野に対する理解を深めることができます。提示されたモデルとそのようなモデルの実験には、いくつかのレベルの複雑さがあります。最初のレベルは基本です。ランダム変数の理解につながり、また科学研究の分野の主要な理解を与えます。次のレベルはより複雑で、並列プログラミングと確率的モデリングのより深い理解を提供します。関連する理論的知識が提示され、必要に応じて、追加資料として使用できます。これらはすべて、科学情報学入門用の基本的なツールキットを提供します。そして、結論として、モデルのさらなる研究と改善のための提案をしたいと思います。

6.1。 モデルの線形性とQSの統計パラメーター

この記事で紹介した多相QSモデルは線形ではありません[12]。これは、非線形数学関数maxを含むため、再帰方程式から明らかになります。特にQSの統計パラメーターを計算する場合に、正しいシミュレーション結果を取得する場合は、計算に部分線形モデルを使用する必要があります。これは、ロードされていないトランスポートシステムにとって特に重要です。そうしないと、計算でかなり大きな誤差が生じる可能性があるためです。

6.2。 Pythonモジュールの拡張機能とCプログラミング

熟練した学生にとって、プログラムコードの有効性を改善し続けることは興味深いかもしれません。これは、SWINGテクノロジーを使用して実装されたC関数でPythonモジュールを拡張することで実行できます。Cython、Cプログラミング言語、「実際の」MPIテクノロジー、およびクラスターシステムのHTC（高性能コンピューティング）を使用して、コード計算を改善し、計算を高速化することができます[5、28、29]。

6.3。ソフトウェアソリューションの効率性とさらなる開発

このセクションでは、学生はさまざまなソフトウェアソリューションの有効性を調べることができます。このトピックは、並列計算に基づくソフトウェアモデルにとって重要です。学生は、さまざまなソフトウェアモデルの有効性を研究し、段階的にアルゴリズムを改善しようとすることができます。ここでの重要なポイントは、情報フローの数とさまざまなソフトウェアプロセスの計算の比率の研究です。したがって、この比率は、並列コンピューティングを使用したプログラムの最も効果的な開発を構築する上で重要です。別の興味深いトピックは、アルゴリズム構造をHTCクラスター構造に変換する可能性の研究です。



研究の追加タスクとして、著者はQSモデリングを検討します。QSモデリングはモデル化および分析する必要があります。QSの比較的複雑な性質と対応する種類のアプリケーションでは、より広範なプログラミング手法を使用する必要があります。このようにして、継承、カプセル化、ポリモーフィズムなどの一般的なプログラミング概念を実装するための優れた基本プラットフォームが表示されます。一方、コンピューターサイエンスの基本的な理論的概念も強調する必要があります。これらすべてに加えて、QSの統計およびシミュレーションモデリングには、確率理論の分野でのより高度な知識、より多くのコンピューティングリソースの使用、実際の科学的コンピューティング環境の提供、および上級学生に対する優れたモチベーションが必要です。

文学