マルコフ連鎖を使用した帰属

ビジネスチャレンジ

顧客の1人がマーケティングトラフィックチャネルを積極的に使用して、サービスと製品を宣伝しました。 しばらくして、すべてのマーケティングチャネルのデータがBigQueryリポジトリにアップロードされ、彼らと何か面白いことをする時が来たと判断しました。 たとえば、分析モジュールを拡張および変更して、マーケティング費用を最適化します。 特に、マルコフチェーンの助けを借りてチャネルのより複雑な属性を使用する機能を実現するために、当時Googleアナリティクスが存在していなかった、おそらく今も存在しなかった。

ブログでは 、広告チャネルの一般的な帰属の問題について話しました 。 ここでは、マルコフ連鎖の使用のみに焦点を当てます。

マルコフ連鎖

マルコフ連鎖は、確率システムのダイナミクスを研究するための非常にシンプルだがエレガントなツールの1つであり、とりわけ商品の帰属に使用されます。 これについては非常に多く書かれており、インターネット上でそのような帰属を説明する例は非常に簡単です。 私たちのビジネスは、このツールを使用して帰属方法を提示することです。 しかし、最初に、知らない人にとってそれが何であるかについて少し話す必要があります。 そして、この部分は安全にスキップできます。

システムが少数の固定状態にしかならないようにしましょう。 そして、各状態で、このシステムの他の可能な状態への遷移の確率は、厳密かつ明確に決定されます。

これがどのように起こるかを理解するために、Andrei Andreyevich Markov自身（シニア）が調査したシステムの例を考えることができます。 システムとして、彼はテキストに文字が現れるランダムなプロセスを考えました。 モデルの形成の基礎として、彼はテキスト「Eugene Onegin」を使用しました。 直観的には、次の文字の確率は前の文字によって大きく決まります。 たとえば、文字「z」が「h」の後に来ることはめったになく、文字「a」はしばしばあり、「space」と「s」の組み合わせは文学言語では一般に不可能です。 一般に、貧しいアンドレイ・アンドレイエビッチは、どの手紙がどの手紙に続くのかを理解するために、プーシキンによるこの美しい作品のすべての手紙を数える必要がありました。

残っているのは、数学の言語で何が起こっているかを説明することだけです。

離散状態を持つシステムがあるとします $$$S = \ lbrace s_1、s_2、...、s_N \ rbrace$ 。 時間は、各離散時間ステップで、既存の状態の1つへの遷移が発生するように設定されます。 したがって、本質的に、時間を考慮から除外し、状態ジャンプが発生する反復のみを考慮します。 各状態は、システムの任意の状態への遷移の条件付き確率のセットによって記述されます。

$$

$$s_1 = \ lbrace p（s_1 | s_1）、p（s_2 | s_1）、... \ rbrace$$

明確さと有用性を高めるために、人々はこれを遷移確率のマトリックスの形で書き出す傾向があります。

$$

$$M = \ begin {bmatrix} p（s_1 | s_1）＆p（s_1 | s_2）＆... \\ p（s_2 | s_1）＆p（s_2 | s_2）＆... \\ \ vdots＆\ vdots＆\ ddots \ end {bmatrix}$$

または、 Wikipediaの例のように、遷移グラフの形式で：

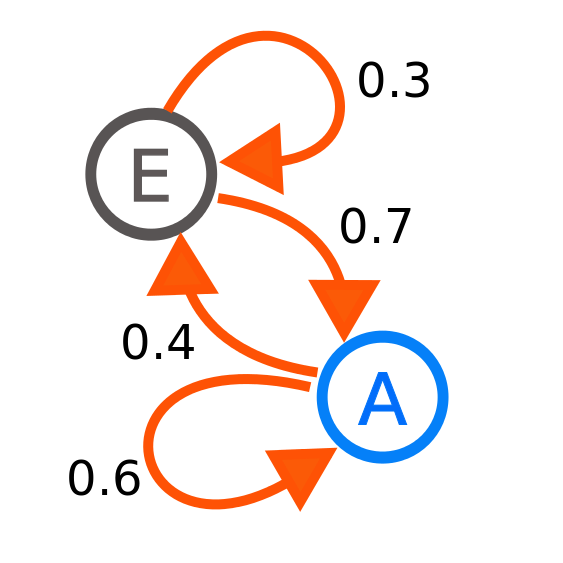
作成者：Joxemai4-自分の作品、CC BY-SA 3.0、 commons.wikimedia.org / w / index.php？curid = 10284158

この図は、2つの状態EとAを持つシステムを示しています。AからAへの遷移の確率は0.6、AからEへの遷移の確率は0.4です。 明らかに、1つの状態からの遷移の条件付き確率の合計は、1に等しくなければなりません。 また、行列Mの各行の合計も1に等しくなければなりません。

しかし、条件付き確率は本当に必要ありません。 システムがどの状態になるかについての絶対的な確率が必要です。 そして、どの状態s0から開始したかがわかっていれば、調べる機会があります。 ゼロのベクトルがあり、現在の状態で統一されています。 これを行うには、システムの最初のステップで、 合計確率の式を使用します。

$$

$$s ^ 1 = s ^ 0 \回M$$

この式から、回帰式は明らかです。これにより、システムの任意のステップで、前のステップからの分布を持つ絶対確率を見つけることができます。 これらの分布は収束することもあれば、収束しないこともあります。 たとえば、上の写真の例では、Eにいる絶対確率は0.3636（36）になり、Aの場合は0.6363（63）になります。

しかし、これは私たちのタスクには当てはまらないので、ここでやめてチャンネルの帰属に移る価値があります。

マルコフ連鎖を使用した帰属

まず、遷移確率マトリックスのコンパイル方法について少しお話しする価値があります。

「Eugene Onegin」の各行はA.マルコフによって慎重に検査されたため、チャネルチェーンとチャネル間の遷移がマトリックスに記録されていると考えます。 たとえば、インデックス1のチャンネルからインデックス2のチャンネルへのチェーンにいる場合、1行2列のマトリックス要素に1が追加されます。

チェーンの統計全体にわたってこの方法で行った場合、結果のマトリックスの各行をこの行の要素の合計で除算し、非常に条件付きの確率を取得します。 そして、実際に帰属方法が始まります。

食べましょう $$$N$ 属性チャネルと計算された遷移確率マトリックス $$$M$ 寸法 $$$（N + 1）×（N + 1）$ 。 $$$（N + 1）$ すべてのチャネルに加えて、「変換」状態への移行もあるためです。 これは最終状態なので、行列の最後の行 $$$M$ はゼロで構成され、最後の要素は1です。さらに、ベクトルがあります $$$L$ -期間全体の変換された属性チェーンの長さの分布。 すなわち もし $$$L_5 = 100、$ つまり、データベースには、コンバージョンで終わる5つの属性チャネルを含む100のチェーンが含まれます。 将来的には以下を使用します。

$$ $$ display $$ \ begin {equation} L '（K）= \ lbrack L_1、L_2、....、L_K \ rbrack / \ sum \ limits_ {k = 1} ^ {K}、L_k \ tag {1 } \ end {equation} $$表示$$

特定のメンバーに正規化 $$$K \ le | L |$ 配布。

各チャンネルについて $$$i \ in 1,2、...、N$ チェーンがこのチャネルで始まる場合、コンバージョンの可能性を示す特定の指標と見なされます。 当然のことながら、ここでの確率という言葉はすでにかなり条件付きで使用されています。これは、他のチャネルの指標と比較できる指標の一部にすぎないためです。 この指標は次のように計算されます。

確率を考慮し始めるチャネルを示すマルコフ連鎖の開始点があるとします。 これはベクトルです。 $$$V_0、| V_0 | = N + 1$ 。 ベクトルはゼロのみで構成され、 $$$V_i ^ 0 = 1$ 。 私たちは1からの長さのチェーンを考慮します $$$K \ le | L |$ 。 各チェーンについて、絶対確率の分布が計算されます。ただし、 $$$V_0$ 。：

$$

$$D_k = D_ {k-1} \回M、\タグ{2}$$

どこで $$$D_k-1$ 上の絶対確率分布 $$$k-1$ チェーンステップ、および（×）は行列乗算です。 明らかに、 $$$D_0 = V_0$ 。 最後のステップでは、ターミナルへの遷移確率を選択します $$$p_ {N + 1、k}$ 初期チャネルの有効性の「尺度」としての条件。 次に、次の式を使用してチャネルのパフォーマンスインジケーターを検討します。

$$

$$E_i = \ sum \ limits_ {k = 1} ^ {K} p_ {N + 1、k} * \チルダ{L} _k、\ tag {3}$$

（*）は要素ごとの乗算であり、 $$$\チルダ{L} = L ’（K）$ 。

この方法で各チャネルのインジケータの値を考慮すると、アレイの効率の比較可能な推定値が得られます $$$E$ 属性に使用できます。 帰属については、チェーン内の各チャネルに以下の重みが割り当てられます $$$E$ さらに重みが正規化されます。 チャンネルインデックスのチェーンがあるとします $$$C$ 同一の隣接チャネルが存在せず、変換で終了します。 その後、次のようにチャネルの属性を計算できます。 ゼロのベクトルを設定します $$$W$ 寸法 $$$N$ 次のように入力します。

$$

$$W_i = \ sum \ limits_ {j = 1} ^ {| C |} \ left \ {\ begin {array} {ll} C_i = 1、if＆i = j \\ C_i = 0、if＆i \ ne j \ end {配列} \右\タグ{4}$$

次に、正規化されたチャネル属性ベクトルは次のように考慮されます。

$$

$$A =（E * W）/ \ sum（E * W）\タグ{5}$$

。

この状況での正規化は、コンバージョンを1つだけと見なすために必要です。 または、もたらされた収入による変換を検討する場合、チャネルに分配された量の収入は収束するはずです。したがって、式（5）には変換収益乗数があります。

例

特定の遷移確率を持つ2つの属性チャネルがあり、それらは遷移確率行列で与えられます。

$$

$$M = \ begin {bmatrix} 0.7＆0.1＆0.2 \\ 0.5＆0.2＆0.3 \\ 0＆0＆1 \ end {bmatrix}、L = \ lbrack 100、50、30、10、5、0、.. 。\ rbrack$$

K = 2を考慮し、式（1）により $$$L ’（2）= \ lbrack 0.67、0.33 \ rbrack$ 。 式（2）に従って、最初のチャネルの長さ1および2のチェーンの絶対確率を計算します。

$$

$$D_ {1,1} = \ begin {bmatrix} 1＆0＆0 \ end {bmatrix} \ times \ begin {bmatrix} 0.7＆0.1＆0.2 \\ 0.5＆0.2＆0.3 \\ 0＆0＆1 \ end {bmatrix} = \ begin {bmatrix} 0.7＆0.1＆0.2 \ end {bmatrix}$$

$$

$$D_ {1,2} = \ begin {bmatrix} 0.7＆0.1＆0.2 \ end {bmatrix} \ times \ begin {bmatrix} 0.7＆0.1＆0.2 \\ 0.5＆0.2＆0.3 \\ 0＆0＆1 \ end {bmatrix} = \ begin {bmatrix} 0.54＆0.09＆0.37 \ end {bmatrix}$$

次に、チャネル効率インジケータは、式（3）によって次のように計算されます。

$$

$$E_1 = 0.2 * 0.67 + 0.37 * 0.33 = 0.256$$

2番目のチャネルの長さ1および2のチェーンの絶対確率を計算します。

$$

$$D_ {2,1} = \ begin {bmatrix} 0＆1＆0 \ end {bmatrix} \ times \ begin {bmatrix} 0.7＆0.1＆0.2 \\ 0.5＆0.2＆0.3 \\ 0＆0＆1 \ end {bmatrix} = \ begin {bmatrix} 0.5＆0.2＆0.3 \ end {bmatrix}$$

$$

$$D_ {2,2} = \ begin {bmatrix} 0.5＆0.2＆0.3 \ end {bmatrix} \ times \ begin {bmatrix} 0.7＆0.1＆0.2 \\ 0.5＆0.2＆0.3 \\ 0＆0＆1 \ end {bmatrix} = \ begin {bmatrix} 0.45＆0.09＆0.46 \ end {bmatrix}$$

次に、チャネルパフォーマンスインジケータは次のように計算されます。

$$

$$E2 = 0.3 * 0.67 + 0.46 * 0.33 = 0.353$$

したがって、完全なチャネルパフォーマンスメトリックベクトル $$$E = [0.256、0.353] ^ T$ 。

チャンネルのチェーンがあると仮定します $$$C = [1,2,1]$ それはコンバージョンで終わります。 次に、式（4）によって：

$$

$$W1 = 1 + 0 + 1 = 2、W2 = 0 + 1 + 0 = 1$$

また、式（5）に従って、このコンバージョンの属性を計算できます。

$$

$$A =（[0.256、0.353] T * [2,1]）/（0.256 * 2 + 0.353 * 1）= [0.59、0.41]。$$

追加

原則として、帰属時に、このチャネルからコンバージョンまでのチェーン内の「距離」に等しいチェーン長の遷移確率に対応する各チャネルの重みを使用できます。 次に、たとえば、上記の例では、属性は次のように考慮されます。

$$

$$A = \ frac {[（D_ {1,1} + D_ {1,3}）、D_ {2,2}]} {D_ {1,1} + D_ {1,3} + D_ {2、 2}} = \ frac {[（0.2 + 0.51）、0.46]} {0.2 + 0.51 + 0.46} = [0.61,0.39]$$

同じことを重みを考慮して行うことができます $$$L ’$ 長さ3のチェーンの場合、次のように計算されます。 $$$L ’（3）= [0.55、0.28、0.17]$ 。 その場合、属性は次のようになります。

$$

$$A = \ frac {[（D_ {1,1} \チルダ{L} _1 + D_ {1,3} \チルダ{L} _3）、D_ {2,2} \チルダ{L} _2]} { D_ {1,1} \チルダ{L} _1 + D_ {1,3} \チルダ{L} _3 + D_ {2,2} \チルダ{L} _2} = \ frac {[（0.2 \ cdot 0.55+ 0.51 \ cdot 0.17）、0.46 \ cdot 0.28]} {0.2 \ cdot 0.55 + 0.51 \ cdot 0.17 + 0.46 \ cdot 0.28} = [0.6,0.4]$$

したがって、このような属性は非常に有用なトラフィック分析ツールとなり、1つのアプローチの枠組み内であっても、さまざまな角度から分析することができます。 このような方法は、目標に簡単に適合し、既知のデータを考慮して補足されます。 たとえば、このアプローチの「開発」の自然な次のステップは、分析に時間を追加し、トランザクション間の時間を考慮することです（特定の期間に遷移がなかった場合の条件付き確率マトリックスの別の中間位置）。 彼らが言うように、人々のためのすべて。

このプロジェクトは、Maxilectが実施した作業の一環として実施されました 。このカテゴリの他のプロジェクトは、こちらでご覧いただけます 。