単純なスペルチェック、またはScalaのLevenshteinメトリックによる辞書から最も近い単語の検索

ご挨拶！ この記事では、レーベンシュタインメトリックの観点から、コーパスから特定の単語に最も近い単語を見つけるアルゴリズムを示します。 形態、コンテキスト、または修正された単語が文に現れる可能性を考慮しないため、単純なスペルチェックと呼ばれますが、最初の近似として完全に低下します。 また、アルゴリズムを拡張して、Char-sの単純なアルファベット以外の他の同等のオブジェクトから最も近いシーケンスを検索することもできます。また、ファイルを処理した後、修正された単語の出現確率を考慮するように適応させることもできます。 ただし、この記事では、英語などの特定のアルファベットの単語の基本的なアルゴリズムに焦点を当てます。



記事のコードはScalaにあります。



猫の下で興味を持っている皆にお願いします。

イントロ

一般的に、VPツリー（Vantage Point Tree）などのメトリック空間で検索するための特殊なデータ構造があります。 ただし、実験では、レーベンシュタインメトリックを使用したワードスペースでは、VPツリーの動作が非常に悪いことが示されています。 その理由は平凡です-このメトリック空間は非常に密です。 たとえば、4文字の単語には、1の距離に膨大な数の近隣があります。距離が遠くなると、オプションの数はセット全体のサイズに匹敵するようになります。 幸いなことに、文字列に対してより最適なソリューションが存在します。これから分析します。

説明

共通の接頭辞を持つ多くの単語をコンパクトに保存するには、trieなどのデータ構造を使用します。





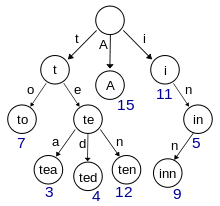
一言で言えば、アルゴリズムは、検索された単語とボア内の単語（トライ）のプレフィックス一致のオプションの暗黙的なグラフでのダイクストラアルゴリズムによる単純な検索として記述されます。 ファジー検索のグラフのノードは上記のオプションになり、エッジの重みは指定された文字列プレフィックスとホウ素ノードの実際のレーベンシュタイン距離になります。

ホウ素の基本的な実装

まず、ホウ素ノードについて説明し、ホウ素内の単語を挿入して明確に検索するアルゴリズムを記述します。 スナックのあいまい検索を残します。

class Trie( val ends: Boolean = false, // whether this node is end of some string private val parent: Trie = null, private val childs : TreeMap[Char, Trie] = null, val value : Char = 0x0)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ご覧のとおり、超自然的なものはありません。 ホウ素ノードは、親への参照、子孫へのMapth参照、ノードのリテラル値、およびノー​​ドが文字列の最終ノードであるかどうかのフラグを持つオブジェクトです。



次に、ボア内の明確な検索について説明します。

 /// exact search def contains(s: String) = { @tailrec def impl(t: Trie, pos: Int): Boolean = if (s.size < pos) false else if (s.size == pos) t.ends else if (t.childs == null) false else if (t.childs.contains(s(pos)) == false) false else impl(t.childs(s(pos)), pos + 1) impl(this, 0) }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

複雑なことは何もありません。 偶然（t.ends）に出会うか、他に下る場所がないことがわかるまで、ノットの子を下って行きます。



今挿入：

 /// insertion def +(s: String) = { def insert(trie: Trie, pos: Int = 0) : Trie = if (s.size < pos) trie else if (pos == 0 && trie.contains(s)) trie else if (s.size == pos) if (trie.ends) trie else new Trie(true, trie.parent, trie.childs, trie.value) else { val c = s(pos) val children = Option(trie.childs).getOrElse(TreeMap.empty[Char, Trie]) val child = children.getOrElse( c, new Trie(s.size == pos + 1, trie, null, c)) new Trie( trie.ends, trie.parent, children + (c, insert(child, pos + 1)), trie.value) } insert(this, 0) }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ボロンは不変なので、 +関数は新しいボロンを返します。



単語のコーパスからのホウ素の構成は次のようになります。

 object Trie { def apply(seq: Iterator[String]) : Trie = seq.filter(_.nonEmpty).foldLeft(new Trie)(_ + _) def apply(seq: Seq[String]) : Trie = apply(seq.iterator) }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

基本ビルドの準備ができました。

ファジー検索、基本機能

グラフノードについて説明しましょう。

 case class Variant(val pos: Int, val node: Trie)(val penalty: Int)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

Pos-対象となるオプションで目的の行のプレフィックスが終了する位置。 ノード-考慮されるオプションのホウ素接頭辞。 ペナルティ-ラインプレフィックスとボロンプレフィックスのレーベンシュタイン距離。



カリー化されたケースクラスは、equals / hashCode関数が最初の引数リストに対してのみコンパイラーによって生成されることを意味します。 ペナルティとバリアントの違いは考慮されません 。



ペナルティが減少しないグラフノードの列挙は、次のシグネチャを持つ関数によって制御されます。

 def prefixes(toFind: String): Stream[Variant]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

それを実装するために、関数ジェネレーターでStreamを生成する小さなヘルパーを作成します。

  def streamGen[Ctx, A] (init: Ctx)(gen: Ctx => Option[(A, Ctx)]): Stream[A] = { val op = gen(init) if (op.isEmpty) Stream.Empty else op.get._1 #:: streamGen(op.get._2)(gen) }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

次に、上記の関数に渡す検索の不変のコンテキストを実装します。これには、ダイクストラのアルゴリズムによって暗黙的なグラフのノードを反復処理するために必要なすべてのものが含まれています。

  private class Context( // immutable priority queue, Map of (penalty-, prefix pos+) -> List[Variant] val q: TreeMap[(Int, Int), List[Variant]], // immutable visited nodes cache val cache: HashSet[Variant]) { // extract from 'q' value with lowest penalty and greatest prefix position def pop: (Option[Variant], Context) = { if (q.isEmpty) (None, this) else { val (key, list) = q.head if (list.tail.nonEmpty) (Some(list.head), new Context(q - key + (key, list.tail), cache)) else (Some(list.head), new Context(q - key, cache)) } } // enqueue nodes def ++(vars: Seq[Variant]) = { val newq = vars.filterNot(cache.contains).foldLeft(q) { (q, v) => val key = (v.penalty, v.pos) if (q.contains(key)) { val l = q(key); q - key + (key, v :: l) } else q + (key, v :: Nil) } new Context(newq, cache) } // searches node in cache def apply(v: Variant) = cache(v) // adds node to cache; it marks it as visited def addCache(v: Variant) = new Context(q, cache + v) } private object Context { def apply(init: Variant) = { // ordering of prefix queue: min by penalty, max by prefix pos val ordering = new Ordering[(Int, Int)] { def compare(v1: (Int, Int), v2: (Int, Int)) = if (v1._1 == v2._1) v2._2 - v1._2 else v1._1 - v2._1 } new Context( TreeMap(((init.penalty, init.pos), init :: Nil))(ordering), HashSet.empty[Variant]) } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ノードのキューは、単純な不変のTreeMapから作成されます。 キュー内のノードは、ペナルティを増やしてプレフィックスposを減らすことでソートされます。



最後に、ストリームジェネレーター自体：

  // impresize search lookup, returns stream of prefix match variants with lowest penalty def prefixes(toFind: String) : Stream[Variant] = { val init = Variant(0, this)(0) // returns first unvisited node @tailrec def whileCached(ctx: Context): (Option[Variant], Context) = { val (v, ctx2) = ctx.pop if (v.isEmpty) (v, ctx2) else if (!ctx2(v.get)) (Some(v.get), ctx2) else whileCached(ctx2) } // generates graph edges from current node def genvars(v: Variant): List[Variant] = { val replacePass: List[Variant] = if (v.node.childs == null) Nil else v.node.childs.toList flatMap { pair => val (key, child) = pair val pass = Variant(v.pos, child)(v.penalty + 1) :: Nil if (v.pos < toFind.length) Variant(v.pos + 1, child)(v.penalty + {if (toFind(v.pos) == key) 0 else 1}) :: pass else pass } if (v.pos != toFind.length) { Variant(v.pos + 1, v.node)(v.penalty + 1) :: replacePass } else replacePass } streamGen(Context(init)) { ctx => val (best, ctx2) = whileCached(ctx) best.map { v => (v, (ctx2 ++ genvars(v)).addCache(v)) } } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

もちろん、 genvarsは最も注目に値します。 グラフの特定のノードについて、そこから発するエッジを生成します。 この検索オプションのホウ素ノードの子孫ごとに、シンボルを挿入したバリアントを生成します

 val pass = Variant(v.pos, child)(v.penalty + 1)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

そしてキャラクターを置き換える

 Variant(v.pos + 1, child)(v.penalty + {if (toFind(v.pos) == key) 0 else 1})
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

行の終わりに達していない場合は、キャラクターを削除するオプションも生成します

 Variant(v.pos + 1, v.node)(v.penalty + 1)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ファジー検索、使いやすさ

もちろん、一般的な使用のためのプレフィックス機能はほとんど役に立ちません。 多かれ少なかれ有意義に見えるようにするラッパーを作成します。 まず、バリアントの列挙をペナルティの合理的な値に制限して、辞書に適切な置換がほとんどない単語にアルゴリズムがスタックしないようにします。

 def limitedPrefixes(toFind: String, penaltyLimit: Int = 5): Stream[Variant] = { prefixes(toFind).takeWhile(_.penalty < penaltyLimit) }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

次に、プレフィックスではなく完全な一致、つまり、検索する文字列の長さと等しいposを持つオプション、および終了== trueフラグを持つノードが最終ノードを指すオプションでフィルターします。

 def matches(toFind: String, penaltyLimit: Int = 5): Stream[Variant] = { limitedPrefixes(toFind, penaltyLimit).filter { v => v.node.ends && v.pos == toFind.size } }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

最後に、オプションのストリームを単語のストリームに変換します。このため、 Trieクラスでは、見つかった単語を返すコードを記述します。

 def makeString() : String = { @tailrec def helper(t: Trie, sb: StringBuilder): String = if (t == null || t.parent == null) sb.result.reverse else { helper(t.parent, sb += t.value) } helper(this, new StringBuilder) }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

複雑なことは何もありません。 ホウ素の根に到達するまで、ノードの値を書き留めて、親によって上に移動します。



そして最後に：

 def matchValues(toFind: String, penaltyLimit: Int = 5): Stream[String] = { matches(toFind, penaltyLimit).map(_.node.makeString) }
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

合計

マッチ関数は非常に普遍的であると言わなければなりません。 それを使用すると、最も近いKを検索できます。

 matches(toFind).take(k).map(_.node.makeString)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

または、最も近いデルタ、つまりD以下の距離にあるラインを検索します。

 matches(toFind).takeWhile(_.penalty < d).map(_.node.makeString)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

別のアルゴリズムは、文字の挿入/削除/置換に異なる重みを導入することで拡張できます。 特定の置換/削除/挿入カウンターをVariantクラスに追加できます。 トライを一般化して、エンドノードに値を格納し、文字列だけでなく、同等のキータイプのインデックスシーケンスも使用できるようにすることができます。 また、各ボロンノードを満たす確率でマークし（最後のノードでは単語を満たす確率+すべての子孫単語を満たす確率、中間ノードでは子孫確率の合計のみ）、ペナルティを計算するときにこの重みを考慮することができますが、これは既にこの記事の範囲外です。



面白かったと思います。 ここにコード