👩‍💼 🏫 🤾🏽 ウェルフォード法と多次元線形回帰 🏂🏾 🚬 🙇

多次元線形回帰は、機械学習の基本的な方法の1つです。データマイニングの現代の世界はニューラルネットワークと勾配ブースティングによって捕捉されているという事実にもかかわらず、線形モデルは依然としてその中で名誉ある地位を占めています。

この主題に関する以前の出版物では、Wellford法により平均と共分散の正確な推定値を取得する方法を学び、次にこれらの推定値を使用して1次元線形回帰の問題を解決する方法を学びました。もちろん、これらの同じ方法は、多次元線形回帰問題でも使用できます。

いくつかの明らかな利点があるため、線形モデルがよく使用されます。

高速のトレーニングとアプリケーション。
多くの場合、再訓練のリスクを減らすモデルの単純さ。
それらを使用して複合モデルを構築する機能：たとえば、数十万の要因がある場合、それらの線形モデルを適切にトレーニングできます。その予測は、より複雑なアルゴリズムの要因として使用されます（勾配ツリーのブースティングなど）。

さらに、一般的に参照される線形モデルのもう1つの古典的な「利点」があります：解釈可能性。私の意見では、それはやや過大評価されていますが、巨大なニューラルネットワークでの使用を追跡するよりも、線形モデルでどの符号に属性係数があるかを判断する方がはるかに簡単です。

内容

1.多次元線形回帰

多次元線形回帰問題では、観測された実量の未知の依存性（未知の目的関数の値）を復元する必要があります。 $y ^ *$ 材料属性のセットから $f_1、f_2、...、f_m$ 。

通常、個々の観測ごとに、特性の値と目的関数が記録されます。次に、すべての観測の符号の値から、符号の行列を作成できます $X$ 、および目的関数の値から-その値のベクトル $y$ ：

X_{i j} = f_{j} （ x_{i} ） 、 1 l e q i l e q n 、 1 l e q j l e q m

$X_ {ij} = f_j（x_i）、1 \ leq i \ leq n、1 \ leq j \ leq m$

y_{i} = y^{*} （ x_{i} ） 、 1 l e q i l e q n 、 1 l e q j l e q m

$y_i = y ^ *（x_i）、1 \ leq i \ leq n、1 \ leq j \ leq m$

ここに $x_i$ -特定の観察。したがって、マトリックスの行は観測値に対応し、列は符号に対応し、観測値の総数、したがってマトリックスの行は $n$ 。

たとえば、目的関数は特定の日の気温です。記号は、地理的に隣接する地点での前日の温度値です。別の例は、為替レートまたは株式の価格の予測です。最も単純なケースでは、過去の同じ規模の値が再び要因として機能する可能性があります。さまざまな時点で目標値とそれに対応する属性を計算することにより、多くの観測が形成されます。

問題の解決策を見つけることは、いくつかの重要な機能を構築することを意味します $a：\ mathbb {R ^ m} \ rightarrow \ mathbb {R}$ 。ここで線形回帰の問題について話しているので、決定関数は線形であると仮定します。実際、これは、決定関数が、特徴ベクトルと重みベクトルのスカラー積であることを意味します。

a_{w} （ x_{i} ） = s u m_{j = 1}^{m} w_{j} c d o t f_{j} （ x_{i} ）

$a_ {w}（x_i）= \ sum_ {j = 1} ^ {m} w_j \ cdot f_j（x_i）$

したがって、問題の解決策は、特徴量のベクトルです $w = \ langle w_1、w_2、...、w_m \ rangle$ 。

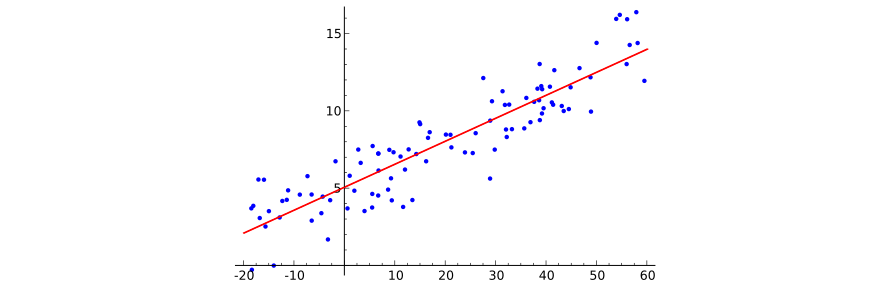
多次元の線形依存をグラフィカルに描くことはかなり困難です（まず、100次元の記号空間を想像してください...）、しかし、1次元の場合の図は、何が起こっているかを理解するのに十分です。このイラストをウィキペディアから借りましょう：

機械学習問題の定式化を完了するには、特定の決定関数が目的関数の値をどれだけうまく予測するかという質問に答える損失関数を示すことだけが必要です。ここで、回帰分析に従来の損失の二乗平均平方根関数を使用します。

Q （ a 、 X 、 y ） = s q r t f r a c 1 n s u m_{i = 1}^{n} （ a （ x_{i} ） - y_{i} ）^{2}

$Q（a、X、y）= \ sqrt {\ frac {1} {n} \ sum_ {i = 1} ^ {n}（a（x_i）-y_i）^ 2}$

したがって、多次元線形回帰のタスクは、重みのセットを見つけることです $w$ 損失関数の値が $Q（a_ {w}、A、y）$ その最小値に達します。

分析のために、通常、ラジカルを放棄し、損失関数で平均化するのが便利です：

Q_{1} （ a 、 X 、 y ） = s u m_{i = 1}^{n} （ a （ x_{i} ） - y_{i} ）^{2}

$Q_1（a、X、y）= \ sum_ {i = 1} ^ {n}（a（x_i）-y_i）^ 2$

さらなる議論のために、関連する要因のセットで観測を特定することが便利です：

x_{i j} = f_{j} （ x_{i} ）

$x_ {ij} = f_j（x_i）$

損失汎関数が単純にスカラー正方形として記述されていることは簡単にわかります。予測のベクトルは次のように記述できます。 $Xw$ 、正解からの逸脱のベクトルは $Xw-y$ 。次に：

Q_{1} （ a 、 X 、 y ） = l a n g l e X w - y 、 X w - y r a n g l e

$Q_1（a、X、y）= \ langle Xw-y、Xw-y \ rangle$

2.ソリューションの一般的な説明

回帰分析から、多次元線形回帰問題のベクトル解が線形代数方程式系の解として見つかることがよく知られています。

（ X^{T} X ） w = X^{T} y

$（X ^ {T} X）w = X ^ {T} y$

証明は簡単です。実際、関数の偏微分を見てみましょう $Q_1$ 重量で $j$ のサイン：

f r a c p a r t i a l Q_{1} p a r t i a l w_{j} = 2 c d o t s u m_{i = 1}^{n} （ l a n g l e w 、 x_{i} r a n g l e - y_{i} ） c d o t x_{i j}

$\ frac {\ partial Q_1} {\ partial w_j} = 2 \ cdot \ sum_ {i = 1} ^ {n}（\ langle w、x_i \ rangle-y_i）\ cdot x_ {ij}$

この導関数をゼロと同等にすると、次のようになります。

s u m_{i = 1}^{n} （ s u m_{k = 1}^{m} w_{k} c d o t x_{i k} - y_{i} ） c d o t x_{i j} = 0

$\ sum_ {i = 1} ^ {n}（\ sum_ {k = 1} ^ {m} w_k \ cdot x_ {ik}-y_i）\ cdot x_ {ij} = 0$

s u m_{i = 1}^{n} B i g （ s u m_{k = 1}^{m} w_{k} c d o t x_{i k} c d o t x_{i j} B i g ） = s u m_{i = 1}^{n} x_{i j} y_{i}

$\ sum_ {i = 1} ^ {n} \ Big（\ sum_ {k = 1} ^ {m} w_k \ cdot x_ {ik} \ cdot x_ {ij} \ Big）= \ sum_ {i = 1} ^ {n} x_ {ij} y_i$

これで、集計順序を変更できます。

s u m_{k = 1}^{m} w_{k} s u m_{i = 1}^{n} B i g （ x_{i k} c d o t x_{i j} B i g ） = s u m_{i = 1}^{n} x_{i j} y_{i}

$\ sum_ {k = 1} ^ {m} w_k \ sum_ {i = 1} ^ {n} \ Big（x_ {ik} \ cdot x_ {ij} \ Big）= \ sum_ {i = 1} ^ { n} x_ {ij} y_i$

の係数が $w_k$ 左は対応する行列要素です $X ^ T X$ ：

s u m_{i = 1}^{n} （ x_{i k} x_{i j} ） = （ X^{T} X ）_{j k}

$\ sum_ {i = 1} ^ {n}（x_ {ik} x_ {ij}）=（X ^ {T} X）_ {jk}$

次に、構築された方程式の右側は、ベクトルの要素です $X ^ T y$ ：

s u m_{i = 1}^{n} x_{i j} y_{i} = （ X^{T} y ）_{j}

$\ sum_ {i = 1} ^ {n} x_ {ij} y_i =（X ^ T y）_j$

したがって、解のすべての成分への偏微分のゼロへの同時等化は、線形代数方程式の望ましいシステムにつながります。

3.ウェルフォード法の適用

SLAUを決定するとき $（X ^ {T} X）w = X ^ {T} y$ さまざまな問題が発生します。たとえば、符号の多重共線性は、行列の縮退につながります $（X ^ {T} X）$ 。さらに、指定されたSLAEを解決する方法を選択する必要があります。

これらの問題について詳しくは説明しません。私の実装では、正則化係数を適応的に選択してリッジ回帰を使用し、SLAEを解決するためにLDL分解法を使用しているとだけ言っておきましょう。

しかし、今ではもっと一般的な問題に興味があります。SLAEの方程式をどのように定式化するのでしょうか？これらの方程式が正しく形成され、計算誤差が小さい場合、選択した方法が適切なソリューションにつながることを期待できます。システムのマトリックスと右側のベクトルを形成する段階ですでにエラーが発生している場合、SLAEを解決する方法は成功しません。

上記から、SLAEをコンパイルするには2つのタイプの係数を計算する必要があることは明らかです。

（ X^{T} X ）_{k j} = s u m_{i = 1}^{n} （ x_{i k} x_{i j} ）

$（X ^ TX）_ {kj} = \ sum_ {i = 1} ^ {n}（x_ {ik} x_ {ij}）$

（ X^{T} y ）_{j} = s u m_{i = 1}^{n} （ x_{i j} y_{i} ）

$（X ^ Ty）_ {j} = \ sum_ {i = 1} ^ {n}（x_ {ij} y_i）$

サンプルが中央にある場合、これらは共分散の式になります。これは最初の記事で言及されました！

一方、サンプルを自分で中央に配置することもできます。させる $X '$ 中心サンプリングの行列であり、 $y '$ -中央サンプリングの応答ベクトル：

x_{i j}^{'} = x_{i j} - f r a c s u m_{k = 1}^{n} x_{k j} n

$x '_ {ij} = x_ {ij}-\ frac {\ sum_ {k = 1} ^ {n} x_ {kj}} {n}$

y_{j}^{'} = y_{j} - f r a c s u m_{k = 1}^{n} y_{k} n

$y '_ {j} = y_ {j}-\ frac {\ sum_ {k = 1} ^ {n} y_k} {n}$

で示す $\ bar {x} _j$ 平均値 $j$ 番目のサイン、そして $\ bar {y}$ -目的関数の平均値：

b a r x_{j} = f r a c 1 n s u m_{k = 1}^{n} x_{k j}

$\ bar {x} _j = \ frac {1} {n} \ sum_ {k = 1} ^ {n} x_ {kj}$

b a r y = f r a c 1 n s u m_{k = 1}^{n} y_{k}

$\ bar {y} = \ frac {1} {n} \ sum_ {k = 1} ^ {n} y_ {k}$

中心問題の解を係数のベクトルとする $w '$ 。それから $i$ イベントの場合、予測値は次のように計算されます。

a^{'} （ x^{'} ） = s u m_{j = 1}^{m} x_{j}^{'} c d o t w_{j}^{'} = s u m_{j = 1}^{m} （ x_{j} - b a r x_{j} ） c d o t w_{j}^{'} = s u m_{j = 1}^{m} x_{j} c d o t w_{j}^{'} - s u m_{j = 1}^{m} b a r x_{j} c d o t w_{j}^{'}

$a '（x'）= \ sum_ {j = 1} ^ m {x'_j \ cdot w'_j} = \ sum_ {j = 1} ^ m {（x_j-\ bar {x} _j）\ cdot w'_j} = \ sum_ {j = 1} ^ m {x_j \ cdot w'_j}-\ sum_ {j = 1} ^ m {\ bar {x} _j \ cdot w'_j}$

同時に $a '（x'）$ 中央値に近似します。ここから、最終的に元の問題の解決策を書き留めることができます。

a （ x ） = s u m_{j = 1}^{m} x_{j} c d o t w_{j}^{'} - s u m_{j = 1}^{m} b a r x_{j} c d o t w_{j}^{'} + b a r y

$a（x）= \ sum_ {j = 1} ^ m {x_j \ cdot w'_j}-\ sum_ {j = 1} ^ m {\ bar {x} _j \ cdot w'_j} + \ bar { y}$

したがって、Wellford法に従って平均と共分散を計算するための式を使用して、中央のケースの線形回帰係数を取得できます。次に、導出された式に従って、中心から外れた場合の解に簡単に変換されます。すべての属性の係数は値を保持しますが、自由係数は式によって計算されます

b a r y - s u m_{j = 1}^{m} b a r x_{j} c d o t w_{j}^{'}

$\ bar {y}-\ sum_ {j = 1} ^ m {\ bar {x} _j \ cdot w'_j}$

4.実装

前回お話ししたのと同じプログラムに多次元線形回帰法の実装を配置しました。

多次元線形回帰法の行列全体が実質的に大きな共分散行列であるという事実を最初に考えたとき、私は本当に各要素を共分散の計算を実装するクラスの個別の実装にしたいと思います。ただし、これは速度の不当な損失につながります。したがって、各標識には $m$ 重みの平均と合計が計算されます。したがって、思考の結果として、次の実現が生まれました。

Wellford多次元線形回帰問題ソルバーは、 TWelfordLRSolver

クラスの形式で実装されます。

 class TWelfordLRSolver { protected: double GoalsMean = 0.; double GoalsDeviation = 0.; std::vector<double> FeatureMeans; std::vector<double> FeatureWeightedDeviationFromLastMean; std::vector<double> FeatureDeviationFromNewMean; std::vector<double> LinearizedOLSMatrix; std::vector<double> OLSVector; TKahanAccumulator SumWeights; public: void Add(const std::vector<double>& features, const double goal, const double weight = 1.); TLinearModel Solve() const; double SumSquaredErrors() const; static const std::string Name() { return "Welford LR"; } protected: bool PrepareMeans(const std::vector<double>& features, const double weight); };

共分散値を更新するプロセスでは、属性の現在の値と次のステップの平均との差を常に処理する必要があるため、これらの値をすべて事前に計算し、それらをいくつかのベクトルに追加するのが論理的です。したがって、クラスには非常に多くのベクトルが含まれます。

要素を追加する場合、最初のステップは、属性の平均値と偏差の値の新しいベクトルを計算することです。

その後、メインマトリックスの要素と右部分のベクトルが更新されます。主対角線と三角形の1つだけがマトリックスから保存されます。それは対称的です。

因子の現在値とその平均値の差はすでに計算され、特別なベクトルに保存されているため、行列を更新する算術演算は非常に簡単です。

算術演算を節約することは、ここで正当化される以上のものです。このマトリックス更新手順は、最もコストがかかるため、漸近的なCPUリソース $O（m ^ 2）$ 。を含むその他の操作右側のベクトルの更新は漸近線形です：

対処する必要がある最後の要素は、重要な機能の形成です。 SLAUソリューションが受信された後、それは最初の非中心のサインに変換されます：

 TLinearModel TWelfordLRSolver::Solve() const { TLinearModel model; model.Coefficients = NLinearRegressionInner::Solve(LinearizedOLSMatrix, OLSVector); model.Intercept = GoalsMean; const size_t featuresCount = OLSVector.size(); for (size_t featureNumber = 0; featureNumber < featuresCount; ++featureNumber) { model.Intercept -= FeatureMeans[featureNumber] * model.Coefficients[featureNumber]; } return model; }

5.実験方法の比較

前回と同様に、Welfordメソッド（ welford_lr

およびnormalized_welford_lr

）に基づく実装は、マトリックスとシステムの右側が標準式（ fast_lr

）を使用して計算される「単純な」アルゴリズムと比較されます。

データディレクトリにあるLIACコレクションの同じデータセットを使用します。データにノイズを導入する同じ方法が使用されます。属性と応答の値に特定の数値が乗算され、その後、それらに異なる数値が追加されます。したがって、計算ケースの観点から問題を取得できます：散布値と比較して大きな平均値。

research-lr

モードでは、サンプルは連続して数回変化し、そのたびにスライド制御手順が開始されます。チェックの結果は、テストサンプルの決定係数の平均値です。

たとえば、kin8nmサンプルの場合、結果は次のとおりです。

 linear_regression research-lr --features kin8nm.features injure factor: 1 injure offset: 1 fast_lr time: 0.002304 R^2: 0.41231 welford_lr time: 0.003248 R^2: 0.41231 normalized_welford_lr time: 0.003958 R^2: 0.41231 injure factor: 0.1 injure offset: 10 fast_lr time: 0.00217 R^2: 0.41231 welford_lr time: 0.0032 R^2: 0.41231 normalized_welford_lr time: 0.00398 R^2: 0.41231 injure factor: 0.01 injure offset: 100 fast_lr time: 0.002164 R^2: -0.39518 welford_lr time: 0.003296 R^2: 0.41231 normalized_welford_lr time: 0.003846 R^2: 0.41231 injure factor: 0.001 injure offset: 1000 fast_lr time: 0.002166 R^2: -1.8496 welford_lr time: 0.003114 R^2: 0.41231 normalized_welford_lr time: 0.003978 R^2: 0.058884 injure factor: 0.0001 injure offset: 10000 fast_lr time: 0.002165 R^2: -521.47 welford_lr time: 0.003177 R^2: 0.41231 normalized_welford_lr time: 0.003931 R^2: 0.00013929 full learning time: fast_lr 0.010969s welford_lr 0.016035s normalized_welford_lr 0.019693s

したがって、サンプルの比較的小さな変更（対応するシフトを使用して100倍にスケーリング）でも、標準メソッドの動作不能につながります。

さらに、ウェルフォード法に基づくソリューションは、不良データに対して非常に耐性があります。すべての最適化により、Wellfordメソッドの平均作業時間は、標準メソッドの平均作業時間よりも50％だけ長くなっています。

Welfordの「正規化された」方法がうまく機能しないこと、さらに加えて、それが最も遅いことがわかります。

おわりに

今日、多次元線形回帰問題の解決方法を学び、その中にウェルフォード法を適用し、その使用により、「悪い」データセットに対しても高い精度の解を達成できることを確認しました。

明らかに、タスクで膨大な数の線形モデルを自動的に構築する必要があり、各モデルの品質を厳密に監視する機会がなく、追加の実行時間が決定的でない場合は、Wellfordメソッドを使用してより信頼性の高い結果を得る必要があります。

文学

habrahabr.ru：ウェルフォード法による平均と共分散の正確な計算
habrahabr.ru：ウェルフォードの方法と一次元線形回帰
github.com：さまざまな計算方法を使用した線形回帰問題ソルバー
github.com：コネクショニスト人工知能研究所（LIAC）のARFFデータセットのコレクション
machinelearning.ru：多次元線形回帰

ウェルフォード法と多次元線形回帰

内容