さまざまな数学的背景を持つ人々がHabrahabrを見ているという事実を念頭に置いて、しかし、線形変換のトピックは実際的な重要性のために彼らの興味のある分野に落ちるかもしれません。
物語を続ける

水の上にある三角形のボート、帽子、釣り竿は、哲学者である数学者を驚かせ、魔法のように凍りついた。
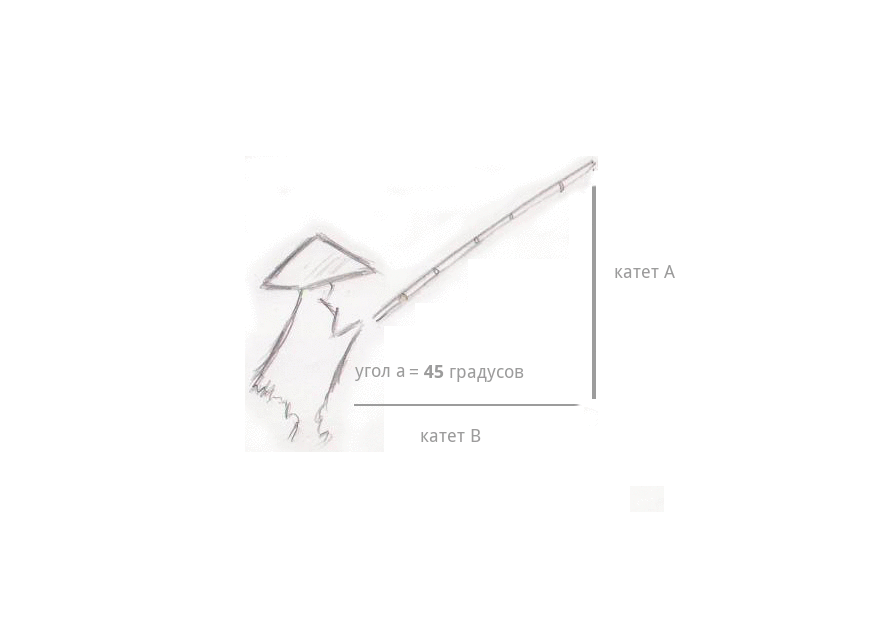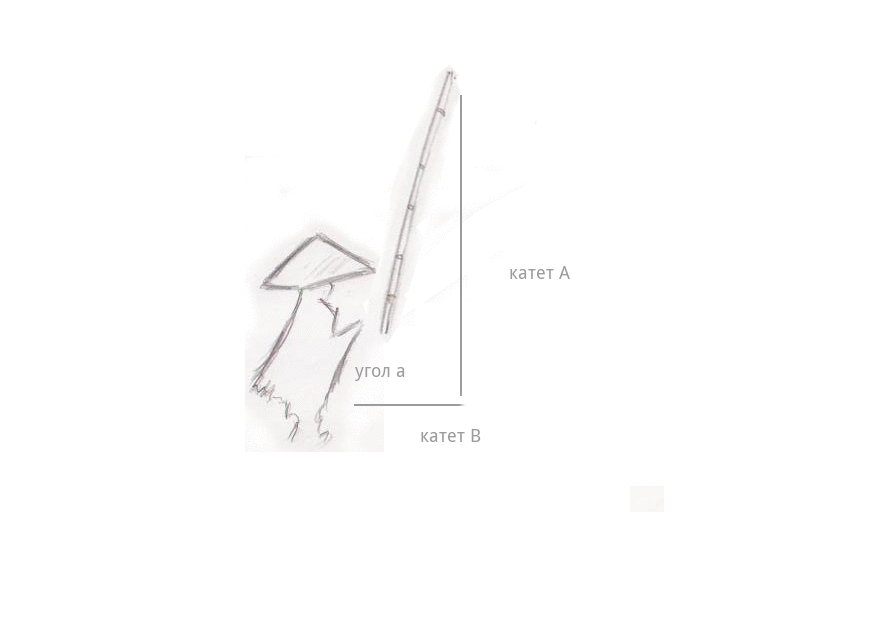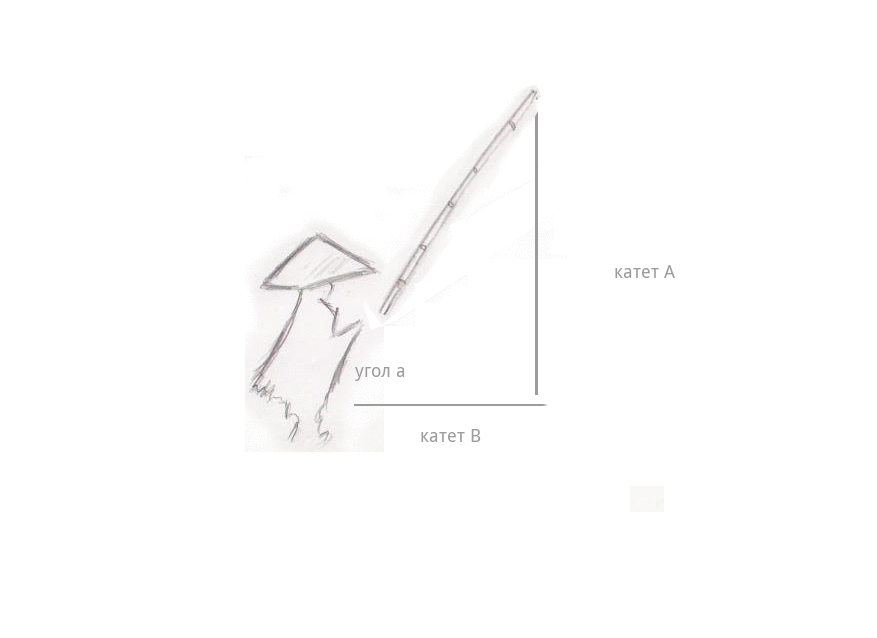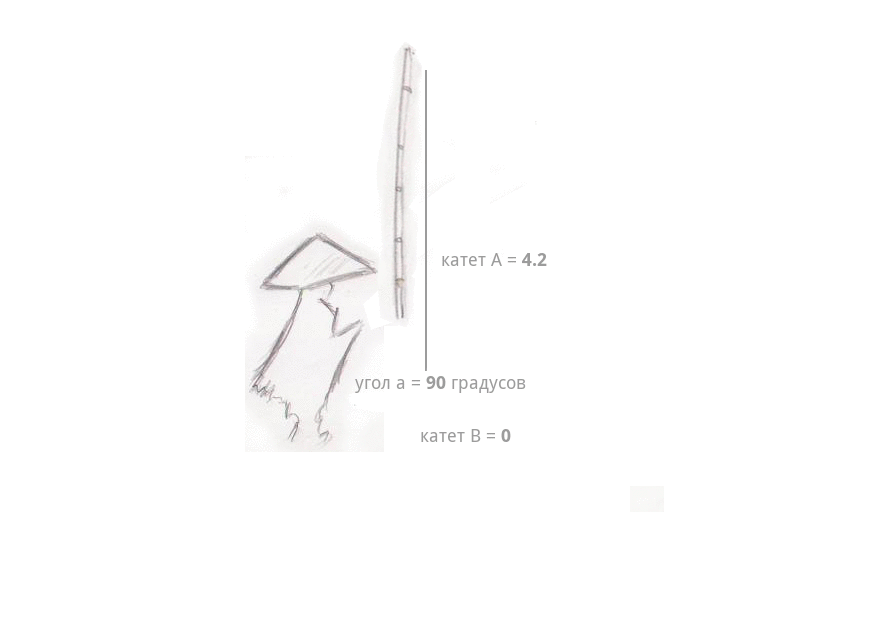
漁師の釣り竿は、黄河の表面に45度の角度できれいに浮かびました。
わずかな霧が水の上に広がりました...そして突然-うなずきました。 漁師は釣り竿を引っ張ると、すぐに身長が上がり始め、釣り糸の長さ(脚A)が目の前で伸び始め、漁師から釣り糸自体までの距離が短くなり始めました(脚B)。 そして、最も興味深いのは、釣り竿自体の長さはまったく変わっていません-空中に弧を描き、漁師の頭の上にほぼ90度の角度であったとしても、伸縮式の釣り竿はまだありませんでした。 釣り糸の長さは釣り竿の長さに等しく、すでにリールがありました-そして、漁師と釣り糸の間の距離は0に変わり、釣り糸は漁師の手にありました。
最後の点は、釣り竿のベクトルに回転行列を掛けると何が起こるかを理解するために非常に重要です。
私たちは懐かしく、さらに考えます...
ピタゴラスの定理を思い出してください。釣り竿の長さの2乗は、脚の2乗の合計です。釣り糸そのものと、漁師と釣り糸が水に浸かる場所との間の距離-C ^ 2 = A 2乗+ B 2乗。
釣り竿の長さが4.2で、釣り糸の長さ(または水面上の高さ)が3で、漁師と釣り糸が水に浸かっている場所との間の距離も3であるとします。
検索に飛び込む
1)釣り糸の長さと釣り竿の長さの関係- 角度aのサイン 。
2)漁師と釣り糸が浸された場所との間の線の長さが釣り竿- コサインaの長さに対応する方法を見つけます。 私達は考慮します:
sin(a)= 3 / 4.2 = 0.7
cos(a)= 3 / 4.2 = 0.7
推測しましょう
脚Aが罪(a)で分割されるとどうなりますか?! すなわち:
3 / 0.7 = 4.2
釣り竿の長さ-斜辺を取得します。
そして、脚Aに罪(a)を掛けると?!
3 * 0.7 = 2.1
斜辺上のこの距離に注意してください-2.1 。
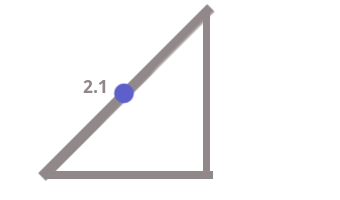
残りの距離も明らかであるため、 -2.1を占めます。
4.2-2.1 = 2.1
これは、現在、正弦と余弦が斜辺を分割することを意味します。 斜辺の二乗は4.2 * 4.2なので、問題は次のとおりです 。4.2に2.1を掛けるとどうなりますか?! 脚の1つが接続されているまさにその部分で:
4.2 * 2.1 = 9(ルート:3)
2番目の脚についても同じです。
足を見つけました。 そして、彼らはピタゴラスの時代から何も変わっていないと確信していました。
次へ
もう一度、 Aの足にsin(a)を掛け、 B の足にcos(a)を掛けます。
3 * 0.7 = 2.1
3 * 0.7 = 2.1
要約:
2.1 + 2.1 = 4.2
または
3 * 0.7 + 3 * 0.7 = 4.2
再び、釣竿の長さに等しい数を取得しました...そして、回転行列に近づきました。
式を思い出す

(ウィキペディアの画像。 記事へのリンク )
下の部分を取ります-ポイントyを取得します:
y = x * sin()+ y * cos()
そして、上記の計算と比較してください:
3 * 0.7 + 3 * 0.7 = 4.2
y = x * sin()+ y * cos()
2滴の水が好きです。 この場合のYは4.2に等しくなります。
式の最初の部分を計算に適用すると、次のようになります。
3 * 0.7-3 * 0.7 = 0
つまり、次のようになります。
xは0になります-漁師は釣り糸をキャッチします。
yは4.2になります-ラインは釣り竿の長さに等しくなります。
xを計算するには、サインとコサインが入れ替わることを忘れないでください。
この場合のisは45度(= 0.7)に等しく、この角度ではサインとコサインは等しく、これは例えば便利です。 他の場合では、明らかに、サインとコサインの値は異なります。 たとえば、40度の場合:cosdegree(40)= 0.7660444431、sindegree(40)= 0.6427876097(同意しない場合はYandexにお問い合わせください。計算機を使用しました)。
最後に
式をx、yの新しい値に数回適用します-サイクルで、毎回45度ずつ、円の動きをはっきりと見ることができます。
釣り竿のベクトルを1度シフトする場合は、式の代わりにを使用します。
三角関数の計算はどうですか?!
ご存知のように、角度のコサインとサインを計算するために、既製の関数が通常使用されます。 リンク情報によると、計算と精度はシステムに依存します。 UNIXシステムの場合、少なくとも2つのオプションがあります。IBMの腸で書かれた関数と、Assemblerの組み込みfsin命令です。 かなり明確なコードとコメントを含むfdlibmライブラリもあります。これは、サインとコサインがこのライブラリで数字piを介して計算されることを示しています。
この記事の著者がすべてを思いついたらどうなりますか?
コンピューターにWebサーバーとPHPインタープリターがある場合は、CSS divブロックを回転させる次のコードを試すことができます。
Index.phpファイル
タイトルスポイラー
<?php if (isset($_GET['ok'])) { $x= $_GET['x']*cos(1)-$y=$_GET['y']*sin(1); $y= $_GET['x']*sin(1)+$y=$_GET['y']*cos(1); } ?>
<style> #rotation_martix { position: absolute; top: <?=$x+300?>px; left: <?=$y+300?>px; background-color: #999; width: 10px; height: 10px; } </style>
< div id="rotation_martix"> </ div> <form method="GET" > <input type="submit" name="ok" value="ok"> <input type="text" name="x" value="<?=$x?>"> <input type="text" name="y" value="<?=$y?>"> </form>
マトリックスをわずかに変更すると、らせん状に回転したり、点から振り子を作成したりできます。