公開鍵暗号に精通している人は、おそらく頭字語ECC 、 ECDH、およびECDSAに精通しているでしょう。 最初は楕円曲線暗号（楕円曲線の暗号）の略語で、残りはそれに基づくアルゴリズムの名前です。



今日、楕円曲線暗号システムは、 TLS 、 PGP 、およびSSHで使用されています 。これらは、現代のWebおよびITの世界が基盤とする最も重要な技術です。 ビットコインやその他の暗号通貨については話していない。



ECCが普及する前は、ほとんどすべての公開キーアルゴリズムは、モジュラー演算に基づく代替暗号システムであるRSA、DSA、およびDHに基づいていました。 RSAと会社は今でも人気があり、多くの場合ECCと組み合わせて使用​​されます。 しかし、RSAや類似のアルゴリズムの基礎となる魔法は多くの人に説明しやすく理解しやすく、 失礼な実装は非常に簡単に書かれているという事実にもかかわらず、ECCの基本はまだほとんどの人にとって謎です。



この一連の記事では、楕円曲線の暗号化の世界の基礎を紹介します。 私の目標は、ECCの完全で詳細なガイドを作成することではなく（インターネットはこのトピックに関する情報でいっぱいです）、 ECCの簡単な概要と、それが安全であると考えられる理由の説明です 。 長い数学的証明や退屈な実装の詳細に時間を費やしません。 また、視覚的なインタラクティブツールとスクリプトを使用した便利な例を示します。



特に、次のトピックを検討します。

1. 実数と群則上の楕円曲線
2. 有限体上の楕円曲線と離散対数問題
3. キーペアの生成と2つのECCアルゴリズム：ECDHおよびECDSA
4. ECCハッキングアルゴリズムとRSAとの比較

この記事を理解するには、集合論、幾何学、モジュラー算術の基礎を理解し、対称および非対称暗号化の原理を理解する必要があります。 最後に、「単純な」タスクと「複雑な」タスクが何であるか、および暗号化におけるそれらの役割を明確に理解する必要があります。



準備はいい？ さあ始めましょう！

パート1：実数と群則上の楕円曲線

楕円曲線

まず、楕円曲線とは何ですか？ Wolfram MathWorldには優れた包括的な定義があります。 しかし、楕円曲線は、方程式で記述された点のセットであるだけで十分です。

$$

$$y ^ 2 = x ^ 3 + ax + b$$

どこで $$$4a ^ 3 + 27b ^ 2 \ ne 0$ 、（これは特別な曲線を除外するために必要です）。 上記の方程式は、楕円曲線の通常のワイエルシュトラス定式化と呼ばれます。









楕円曲線の異なる形状（ $$$b = 1$ 、 $$$a$ 2から-3まで変化します。









特徴の種類：左側-戻り点のある曲線（尖点）（ $$$y ^ 2 = x ^ 3$ ） 右側には自己交差曲線（ $$$y ^ 2 = x ^ 3-3x + 2$ ） これらの例は両方とも完全な楕円曲線ではありません。



値に応じて $$$a$ そして $$$b$ 楕円曲線は、平面上で異なる形状を取ることができます。 簡単に確認および検証できるように、楕円曲線は軸に対して対称です。 $$$X$ 。



目的のために、 無限遠点 （理想点とも呼ばれる） が曲線の一部である必要もあります。 これからは、シンボル0（ゼロ）で無限遠のポイントを示します。



無限大の点を明示的に考慮する必要がある場合、楕円曲線の定義は次のように明確にできます。

$$

$$\左\ {（x、y）\ in \ mathbb {R} ^ 2 \ | \ y ^ 2 = x ^ 3 + ax + b、\ 4 a ^ 3 + 27 b ^ 2 \ ne 0 \右\ } \ \カップ\ \左\ {0 \右\}$$

グループ

数学では、グループは「加算」と呼ばれる+で表されるバイナリ演算を定義したセットです。 設定するには $$$\ mathbb {G}$ グループであった場合、次の4つのプロパティに対応するように追加を定義する必要があります。

1. 回路： if $$$a$ そして $$$b$ 含まれています $$$\ mathbb {G}$ それから $$$a + b$ に含まれる $$$\ mathbb {G}$ ;
2. 結合性： $$$（a + b）+ c = a +（b + c）$ ;
3. ユニット要素 0があり、 $$$a + 0 = 0 + a = a$ ;
4. 各要素には逆値があります 。つまり、 $$$a$ そのようなものがあります $$$b$ あれ $$$a + b = 0$ 。

5番目の要件を追加する場合：

1. 可換性： $$$a + b = b + a$ 、

そのグループはアーベル群と呼ばれます。



通常の追加では、整数のセット $$$\ mathbb {Z}$ グループです（さらに、それはアーベルのグループです）。 多くの自然数 $$$\ mathbb {N}$ ただし、4番目のプロパティを満たさないため、グループではありません。



グループは、4つのプロパティすべてに準拠していることが証明されると、「負荷に対して」他のプロパティを自動的に受け取るという点で便利です。 たとえば、 単一の要素は一意です。 さらに、 相互の値は一意です 。つまり、それぞれに対して $$$a$ ただ一つ $$$b$ そのような $$$a + b = 0$ （そして私たちは書くことができます $$$b$ どうやって $$$-a$ ） 直接的または間接的に、これらおよびグループの他のプロパティは、将来的に非常に役立ちます。

楕円曲線の群則

楕円曲線のグループを定義できます。 すなわち：

• グループの要素は楕円曲線の点です。
• 単一の要素は無限遠点0です。
• 点の逆数 $$$P$ 軸に関して対称な点です $$$x$ ;
• 加算は、次のルールによって定義されます。3つの非ゼロポイントの合計 $$$P$ 、 $$$Q$ そして $$$R$ 一直線上に横たわると等しい $$$P + Q + R = 0$ 。

1つの直線上にある3つのポイントの合計は0です。



最後のルールでは、1つの直線上に3つのポイントのみが必要であり、これらの3つのポイントの順序は重要ではないことを考慮する価値があります。 これは、3つのポイントが $$$P$ 、 $$$Q$ そして $$$R$ 一直線上に横たわる $$$P +（Q + R）= Q +（P + R）= R +（P + Q）= \ cdots = 0$ 。 したがって、 演算子+が結合性と可換性の特性を持っていることを直感的に証明しました：私たちはアーベル群に属しています。



これまでのところ、すべてが順調に進んでいます。 しかし、2つの任意のポイントの合計をどのように計算しますか？

幾何学的な加算

私たちはアーベル群に属しているという事実のために、私たちは書くことができます $$$P + Q + R = 0$ どうやって $$$P + Q = -R$ 。 この形式のこの方程式により、2点の合計を計算する幾何学的な方法を導き出すことができます。 $$$P$ そして $$$Q$ ： を介して線を引く場合 $$$P$ そして $$$Q$ 、この線は曲線の3番目の点と交差します $$$R$ （これは、 $$$P$ 、 $$$Q$ そして $$$R$ 同じ行にあります） 。 この点の逆数をとると $$$-R$ 私たちは量を見つけます $$$P + Q$ 。









直線を描く $$$P$ そして $$$Q$ 。 線は3番目の点を横切る $$$R$ 。 彼女のポイントに対称 $$$-R$ 結果です $$$P + Q$ 。



幾何学的手法は機能しますが、改善が必要です。 特に、いくつかの質問に答える必要があります。

• もしも $$$P = 0$ または $$$Q = 0$ ？ もちろん、直線を描くことはできません（0は平面上にありません $$$xy$ ） しかし、0を単一の要素として定義したため、 $$$P + 0 = P$ そして $$$0 + Q = Q$ のために $$$P$ および $$$Q$ 。
• もしも $$$P = -Q$ ？ この場合、2つのポイントを通る線は垂直で、3番目のポイントと交差しません。 しかし、もし $$$P$ はの逆です $$$Q$ それから $$$P + Q = P +（-P）= 0$ 相互の定義から。
• もしも $$$P = Q$ ？ この場合、無限の数の線が点を通過します。 ここでは、事態はもう少し複雑になります。 しかし、そのポイントを想像してください $$$Q '\ ne P$ 。 強制するとどうなりますか $$$Q '$ 努力する $$$P$ 彼女に近づいて？
  
  
  
  
  
  
  
  
  
  
  
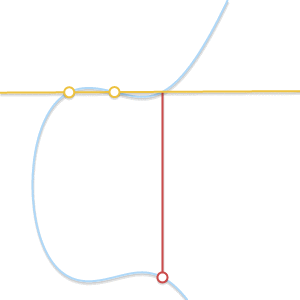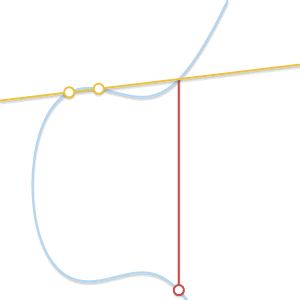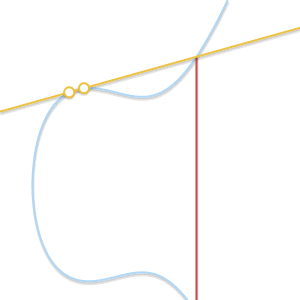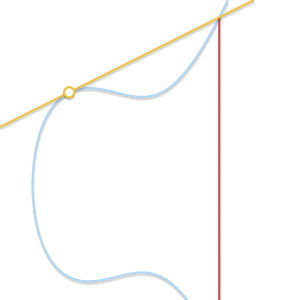
  2つの点が互いに近づくと、それらを通る線は曲線の接線になります。
  
  
  
  以来 $$$Q '$ にコミット $$$P$ まっすぐに $$$P$ そして $$$Q '$ 曲線の接線になります。 これに照らして、私たちはそれを言うことができます $$$P + P = -R$ どこで $$$R$ 曲線と曲線の接線との交差点は $$$P$ 。
• もしも $$$P \ ne Q$ しかし、第三のポイント $$$R$ いや？ この場合、状況は前の状況と似ています。 実際、この状況では、通過するラインは $$$P$ そして $$$Q$ 曲線の接線です。
  
  
  
  
  
  
  
  
  
  
  
  線が2点のみと交差する場合、これは曲線に接していることを意味します。 加算の結果が2つのポイントのいずれかに対称になる方法は簡単にわかります。
  
  
  
  と仮定する $$$P$ タッチポイントです。 前のケースでは、記録しました $$$P + P = -Q$ 。 この方程式は、次のようになります。 $$$P + Q = -P$ 。 一方、連絡先が $$$Q$ 方程式は正しいでしょう $$$P + Q = -Q$ 。

これで幾何学的手法が完成し、すべてのケースが考慮されます。 鉛筆と定規を使用して、楕円曲線のすべての点を追加できます。 試してみたい場合は、楕円曲線の合計を計算するために作成したHTML5 / JavaScriptビジュアルツールをご覧ください 。

代数加算

コンピューターに点の追加を処理させるには、幾何学的手法を代数的手法に変換する必要があります。 上記のルールを一連の方程式に変換することは簡単に思えるかもしれませんが、実際には、3次方程式を解く必要があるため、かなり面倒です。 したがって、結果のみを表示します。



始めるために、最も厄介なデッドロックを取り除きましょう。 私たちはすでにそれを知っています $$$P +（-P）= 0$ 、そして私たちはそれを知っています $$$P + 0 = 0 + P = P$ 。 したがって、方程式では、これらの2つのケースを回避し、2 つの非ゼロの非対称ポイントのみを考慮します。 $$$P =（x_P、y_P）$ そして $$$Q =（x_Q、y_Q）$ 。



もし $$$P$ そして $$$Q$ 一致しない （ $$$x_P \ ne x_Q$ ）、それらを通る直線には勾配があります ：

$$

$$m = \ frac {y_P-y_Q} {x_P-x_Q}$$

この線と楕円曲線の交点が 3番目の点です $$$R =（x_R、y_R）$ ：

$$

$$\ begin {array} {rcl} x_R＆=＆m ^ 2-x_P-x_Q \\ y_R＆=＆y_P + m（x_R-x_P）\ end {array}$$

または同様に：

$$

$$y_R = y_Q + m（x_R-x_Q）$$

だから $$$（x_P、y_P）+（x_Q、y_Q）=（x_R、-y_R）$ （兆候に注意を払い、それを覚えておいてください $$$P + Q = -R$ ）



結果の正確性を検証する必要がある場合、次のことを確認する必要があります。 $$$R$ 曲線とかどうか $$$P$ 、 $$$Q$ そして $$$R$ 一直線上に。 1行であることの検証は簡単で、所属の検証は $$$R$ 曲線-いいえ、3次方程式を解かなければならないので、これは完全に悲しいことです。



代わりに、例を試してみましょう： 視覚ツールによると、 $$$P =（1、2）$ そして $$$Q =（3,4）$ 曲線に属する $$$y ^ 2 = x ^ 3-7x + 10$ 、それらの合計は等しい $$$P + Q = -R =（-3,2）$ 。 これが方程式と一致するかどうかを確認しましょう：

$$

$$\ begin {array} {rcl} m＆=＆\ frac {y_P-y_Q} {x_P-x_Q} = \ frac {2-4} {1-3} = 1 \\ x_R＆=＆m ^ 2- x_P-x_Q = 1 ^ 2-1-3 = -3 \\ y_R＆=＆y_P + m（x_R-x_P）= 2 + 1 \ cdot（-3-1）= -2 \\＆=＆y_Q + m（x_R-x_Q）= 4 + 1 \ cdot（-3-3）= -2 \ end {array}$$

はい、そうです！



これらの方程式は、 ポイントが $$$P$ または $$$Q$ タッチポイントです。 確認しましょう $$$P =（-1、4）$ そして $$$Q =（1、2）$ 。

$$

$$\ begin {array} {rcl} m＆=＆\ frac {y_P-y_Q} {x_P-x_Q} = \ frac {4-2} {-1-1} = -1 \\ x_R＆=＆m ^ 2-x_P-x_Q =（-1）^ 2-（-1）-1 = 1 \\ y_R＆=＆y_P + m（x_R-x_P）= 4 + -1 \ cdot（1-（-1）） = 2 \ end {array}$$

結果が出ました。 $$$P + Q =（1、-2）$ 、 視覚ツールで得られた結果と一致します 。



その機会に $$$P = Q$ 少し異なる方法で処理する必要があります。 $$$x_R$ そして $$$y_R$ 同じままですが、それを考慮して $$$x_P = x_Q$ 傾斜には別の方程式を使用する必要があります。

$$

$$m = \ frac {3 x_P ^ 2 + a} {2 y_P}$$

ご想像のとおり、この式は $$$m$ は一階微分です：

$$

$$y_P = \ pm \ sqrt {x_P ^ 3 + ax_P + b}$$

この結果の正確性を証明するには、次のことを検証するだけで十分です。 $$$R$ 曲線に属し、その線が通過する $$$P$ そして $$$R$ 曲線との交差点は2つだけです。 しかし、ここでもそれを証明せず、代わりに例を分析します。 $$$P = Q =（1、2）$ 。

$$

$$\ begin {array} {rcl} m＆=＆\ frac {3x_P ^ 2 + a} {2 y_P} = \ frac {3 \ cdot 1 ^ 2-7} {2 \ cdot 2} = -1 \\ x_R＆=＆m ^ 2-x_P-x_Q =（-1）^ 2-1-1 = -1 \\ y_R＆=＆y_P + m（x_R-x_P）= 2 +（-1）\ cdot（- 1-1）= 4 \ end {array}$$

私たちに与えるもの $$$P + P = -R =（-1、-4）$ 。 そう！



結果を取得する手順は非常に面倒ですが、方程式は非常に簡単です。 これはすべて、Weierstrassの通常の定式化のおかげです。これがないと、これらの方程式は非常に長く複雑になります。

スカラー乗算

加算に加えて、別の演算を定義できます： スカラー乗算 、つまり：

$$

$$nP = \アンダーブレース{P + P + \ cdots + P} _ {n \ \ text {times}}$$

どこで $$$n$ 自然数です。 また、スカラー乗算用の視覚ツールも作成したので、試してみてください。



この形式で書くとき、計算は明らかです $$$nP$ が必要です $$$n$ 追加。 もし $$$n$ から成る $$$k$ 小数点以下の場合、アルゴリズムは複雑になります $$$O（2 ^ k）$ あまり良くありません。 しかし、より高速なアルゴリズムがあります。



それらの1つは、 倍加加算アルゴリズムです。 その動作の原理は、例を使用して簡単に説明できます。 取る $$$n = 151$ 。 バイナリ形式では、次の形式になります $$$10010111_2$ 。 このようなバイナリ形式は、2の累乗の合計として表すことができます。

$$

$$\ begin {array} {rcl} 151＆=＆1 \ cdot 2 ^ 7 + 0 \ cdot 2 ^ 6 + 0 \ cdot 2 ^ 5 + 1 \ cdot 2 ^ 4 + 0 \ cdot 2 ^ 3 + 1 \ cdot 2 ^ 2 + 1 \ cdot 2 ^ 1 + 1 \ cdot 2 ^ 0 \\＆=＆2 ^ 7 + 2 ^ 4 + 2 ^ 2 + 2 ^ 1 + 2 ^ 0 \ end {array}$$

（すべての2進数を取りました $$$n$ 2のべき乗を掛けます。）



これを念頭に置いて、次のように記述できます。

$$

$$151 \ cdot P = 2 ^ 7 P + 2 ^ 4 P + 2 ^ 2 P + 2 ^ 1 P + 2 ^ 0 P$$

倍加アルゴリズムは、次の手順を定義します。

• 取る $$$P$ 。
• 取得するにはダブル $$$2P$ 。
• 折ります $$$2P$ そして $$$P$ （結果を得るために $$$2 ^ 1P + 2 ^ 0P$ ）
• ダブル $$$2P$ 取得する $$$2 ^ 2P$ 。
• 結果に追加する（取得する $$$2 ^ 2P + 2 ^ 1P + 2 ^ 0P$ ）
• ダブル $$$2 ^ 2P$ 得る $$$2 ^ 3P$ 。
• で追加を実行しないでください $$$2 ^ 3P$ 。
• ダブル $$$2 ^ 3P$ 取得する $$$2 ^ 4P$ 。
• 結果に追加する（取得する $$$2 ^ 4P + 2 ^ 2P + 2 ^ 1P + 2 ^ 0P$ ）
• ...

その結果、計算します $$$151 \ cdot P$ 7回の倍増と4回の追加だけを完了しました。



これが完全に明確でない場合、このアルゴリズムを実装するPythonスクリプトを次に示します。

def bits(n): """    n,     . bits(151) -> 1, 1, 1, 0, 1, 0, 0, 1 """ while n: yield n & 1 n >>= 1 def double_and_add(n, x): """   n * x,   -. """ result = 0 addend = x for bit in bits(n): if bit == 1: result += addend addend *= 2 return result
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

倍増と加算が演算の場合 $$$O（1）$ このアルゴリズムは複雑です $$$O（\ log n）$ （または $$$O（k）$ ビット長を考慮して）、これはかなり良いです。 そしてもちろん、元のアルゴリズムよりもはるかに優れています $$$O（n）$ ！

対数

与えられた $$$n$ そして $$$P$ 少なくとも1つの多項式計算アルゴリズムがあります $$$Q = nP$ 。 しかし、逆問題はどうですか？ もし知っていたら $$$Q$ そして $$$P$ 、そして決定する必要があります $$$n$ ？ この問題は対数問題として知られています 。 他の暗号システムとの一貫性のために、「除算」という用語の代わりに「対数」という言葉を使用します（乗算ではなくべき乗が使用されます）。



対数問題を解決するための単一の「単純な」アルゴリズムは知りませんが、 乗算を実験すると 、いくつかのパターンを簡単に検出できます。 たとえば、曲線を描く $$$y ^ 2 = x ^ 3-3x + 1$ そしてポイント $$$P =（0、1）$ 。 すぐに確認できます $$$n$ 奇妙な $$$nP$ 左半平面の曲線上にあります。 もし $$$n$ それでも $$$nP$ -右半平面。 さらに実験を行うと、この曲線の対数を効率的に計算するためのアルゴリズムを書くことにつながる他のパターンを見つけることができます。



しかし、対数問題にはバリエーションがあります。 離散対数問題です。 次の部分で見るように、楕円曲線の定義の領域を減らすと、 スカラー乗算は「単純」のままであり、離散対数は「難しい」タスクになります 。 このような二重性は、楕円曲線の暗号化の重要な特徴です。



次のパートでは、 有限体と離散対数問題、および実験の例とツールを調べます 。

パート2：有限体上の楕円曲線と離散対数問題

前のパートでは、実数上の楕円曲線を使用してグループを定義する方法について説明しました。 つまり、ポイントの加算ルールを決定しました。1つの直線上にある3つのポイントの合計はゼロです（ $$$P + Q + R = 0$ ） ポイントの加算を計算するための幾何学的および代数的手法を導き出しました。



次に、スカラー乗算の概念を導入しました（ $$$nP = P + P + \ cdots + P$ ）そして、スカラー乗算を計算するための「単純な」アルゴリズムである、2倍加算を見つけました。



次に、楕円曲線を実数ではなく有限体に制限し、その変化を確認します。

pを法とする整数のフィールド

最後のフィールドは、まず、有限数の要素のセットです。 有限体の例は、モジュロを使った整数のセットです $$$p$ どこで $$$p$ 素数です。 一般的に、これは $$$\ mathbb {Z} / p$ 、 $$$Gf（p）$ または $$$\ mathbb {F} _p$ 。 最後のエントリを使用します。



フィールドには、加算（+）と乗算（・）の2つの二重演算があります。 どちらも閉じられており、連想的で可換です。 両方の操作に固有のユニット要素があり、各要素に逆値の固有の要素があります。 そして最後に、乗算は加算に関して分配的です： $$$x \ cdot（y + z）= x \ cdot y + x \ cdot z$ 。



モジュロ整数セット $$$p$ 0からのすべての整数で構成されます $$$p-1$ 。 加算と乗算は、 モジュラー演算のように機能します。 以下に操作の例をいくつか示します $$$\ mathbb {F} _ {23}$ ：

• 追加： $$$（18 + 9）\ bmod {23} = 4$
• 減算： $$$（7-14）\ bmod {23} = 16$
• 乗算： $$$4 \ cdot 7 \ bmod {23} = 5$
• 加法反転： $$$-5 \ bmod {23} = 18$ 。 確かに： $$$（5 +（-5））\ bmod {23} =（5 + 18）\ bmod {23} = 0$
• 乗法反転： $$$9 ^ {-1} \ bmod {23} = 18$

これらの方程式に不慣れで、モジュラー算術の基礎を学びたい場合は、カーンアカデミーでコースを受講してください 。



整数を法として言ったように $$$p$ フィールドであるため、上記のプロパティはすべて保存されます。 その要件は $$$p$ 素数でした、非常に重要です！ 4を法とする整数の集合は体ではありません：2は乗法の反転を持ちません（すなわち、方程式 $$$2 \ cdot x \ bmod {4} = 1$ 決定はありません）。

モジュロp

すぐに楕円曲線を定義します $$$\ mathbb {F} _p$ しかし、最初にそれを明確に理解する必要があります $$$x / y$ 意味する $$$\ mathbb {F} _p$ 。 簡単に言えば： $$$x / y = x \ cdot y ^ {-1}$ 、またはプレーンテキストで、 $$$x$ 分子と $$$y$ 分母の $$$x$ 倍の逆数 $$$y$ 。 これは驚くことではありませんが、除算を行う簡単な方法を提供します： 数値の逆数を見つけてから、単純な乗算を行います。



逆数計算は、 拡張ユークリッドアルゴリズムを使用して「単純に」実行できます。最悪の場合は複雑になります $$$O（\ log p）$ （または $$$O（k）$ ビット長を考慮する場合）。



ユークリッド拡張アルゴリズムの詳細には触れません。これは記事の一部ではありませんが、Pythonでの実用的な実装を紹介します。

 def extended_euclidean_algorithm(a, b): """      (gcd, x, y), ,  a * x + b * y == gcd,  gcd -    a  b.              O(log b). """ s, old_s = 0, 1 t, old_t = 1, 0 r, old_r = b, a while r != 0: quotient = old_r // r old_r, r = r, old_r - quotient * r old_s, s = s, old_s - quotient * s old_t, t = t, old_t - quotient * t return old_r, old_s, old_t def inverse_of(n, p): """    n   p.       m,   (n * m) % p == 1. """ gcd, x, y = extended_euclidean_algorithm(n, p) assert (n * x + p * y) % p == gcd if gcd != 1: #  n  0,  p   . raise ValueError( '{} has no multiplicative inverse ' 'modulo {}'.format(n, p)) else: return x % p
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

楕円曲線 $$$\ mathbb {F} _p$

これで、楕円曲線をフィールドに制限するために必要なすべての要素ができました。 $$$\ mathbb {F} _p$ 。 前のパートでは次の形式であったポイントのセット：

$$

$$\ begin {array} {rcl} \ left \ {（x、y）\ in \ mathbb {R} ^ 2 \ right。 ＆\左。 | \右。 ＆\左。 y ^ 2 = x ^ 3 + ax + b、\右。 \\＆＆\左。 4a ^ 3 + 27b ^ 2 \ ne 0 \ right \} \ \ cup \ \ left \ {0 \ right \} \ end {array}$$

今になります：

$$

$$\ begin {array} {rcl} \ left \ {（x、y）\ in（\ mathbb {F} _p）^ 2 \ right。 ＆\左。 | \右。 ＆\左。 y ^ 2 \ equiv x ^ 3 + ax + b \ pmod {p}、\右。 \\＆＆\左。 4a ^ 3 + 27b ^ 2 \ not \ equiv 0 \ pmod {p} \ right \} \ \ cup \ \ left \ {0 \ right \} \ end {array}$$

ここで、0はまだ無限大の点であり、 $$$a$ そして $$$b$ -2つの整数 $$$\ mathbb {F} _p$ 。









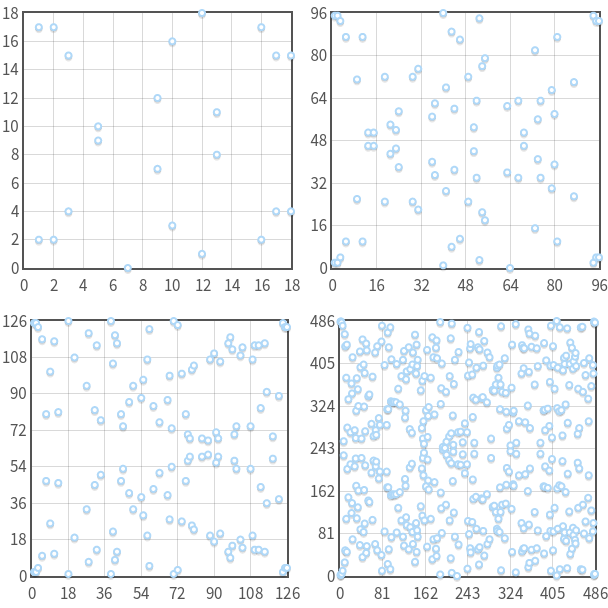
曲線 $$$y ^ 2 \ equiv x ^ 3-7x + 10 \ pmod {p}$ と $$$p = 19、97、127、487$ 。 それぞれに注意してください $$$x$ 最大2つのポイントがあります。 対称性にも注目してください $$$y = p / 2$ 。









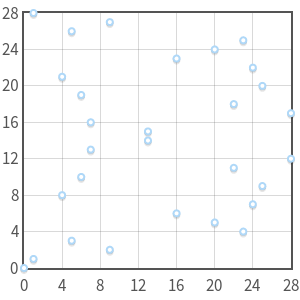
曲線 $$$y ^ 2 \ equiv x ^ 3 \ pmod {29}$ 単数形であり、中に三重点がある $$$（0、0）$ 。 真の楕円曲線ではありません。



以前は連続曲線であったものが、平面上の個々の点のセットになりました $$$xy$ 。 しかし、定義の領域の制限にもかかわらず、 楕円曲線が $$$\ mathbb {F} _p$ まだアーベルグループを作成します 。

ポイント加算

明らかに、追加の定義を少し修正して、 $$$\ mathbb {F} _p$ 。 実数については、1行の3点の合計がゼロ（ $$$P + Q + R = 0$ ） この定義を維持することはできますが、上の1つの直線上に3つのポイントがあるとはどういう意味ですか $$$\ mathbb {F} _p$ ？



それらを結ぶ線があれば、3点は同じ線上にあると言えます 。 もちろん、まっすぐ $$$\ mathbb {F} _p$ 上記の行とは異なります $$$\ mathbb {R}$ 。 上記の行と言えます $$$\ mathbb {F} _p$ たくさんのポイントです $$$（x、y）$ 方程式を満たす $$$ax + by + c \ equiv 0 \ pmod {p}$ （これは、追加された部分を持つ行の標準方程式です $$$（\ text {mod} \ p）$ "）。









曲線に点を追加する $$$y ^ 2 \ equiv x ^ 3-x + 3 \ pmod {127}$ で $$$P =（16、20）$ そして $$$Q =（41、120）$ 。 接続線がどのようにポイントするかに注意 $$$y \ equiv 4x + 83 \ pmod {127}$ 飛行機で「繰り返し」。



私たちがまだグループにいることを考えると、ポイントの追加はすでに知っているプロパティを保存します：

• $$$Q + 0 = 0 + Q = Q$ （単一の要素の定義から）。
• のために $$$Q$ 相互の $$$-Q$ 横座標は同じですが、縦座標が逆のポイントです。 または、必要に応じて、 $$$-Q =（x_Q、-y_Q \ bmod {p}）$ 。 たとえば、曲線が終わった場合 $$$\ mathbb {F} _ {29}$ ポイントがあります $$$Q =（2、5）$ その逆は $$$-Q =（2、-5 \ bmod {29}）=（2、24）$ 。
• また $$$P +（-P）= 0$ （相互の定義から）。

代数の量

ポイントの追加を実行するための方程式は、前の部分とまったく同じですが、各式の最後に追加する必要があることを除きます。 $$$\テキスト{mod} \ p$ 」。したがって、 $$$P =（x_P、y_P）$ 、 $$$Q =（x_Q、y_Q）$ そして $$$R =（x_R、y_R）$ それから $$$P + Q = -R$ 次のように計算できます。

$$

$$\ begin {array} {rcl} x_R＆=＆（m ^ 2-x_P-x_Q）\ bmod {p} \\ y_R＆=＆[y_P + m（x_R-x_P）] \ bmod {p} \\ ＆=＆[y_Q + m（x_R-x_Q）] \ bmod {p} \ end {array}$$

もし $$$P \ ne Q$ その後、斜面 $$$m$ 次の形式を取ります。

$$

$$m =（y_P-y_Q）（x_P-x_Q）^ {-1} \ bmod {p}$$

そうでなければ、 $$$P = Q$ 私達は得る：

$$

$$m =（3 x_P ^ 2 + a）（2 y_P）^ {-1} \ bmod {p}$$

方程式は変更されておらず、これは偶然ではありません。実際、これらの方程式は、有限および無限の両方のフィールドで機能します（ただし、 $$$\ mathbb {F} _2$ そして $$$\ mathbb {F} _3$ 特別なケースです）。 説明する必要があると思います。 しかし、問題があります。グループ法の証明には通常、複雑な数学的概念が必要です。 しかし、最も単純な概念のみを使用するStefan Friedlの証明を見つけました。 これらの方程式がどのフィールドでも（ほぼ）動作する理由に興味がある場合は、それをお読みください。



曲線に戻りましょう-幾何学的な方法を決定しません。実際、問題が発生します。 たとえば、前の部分では、計算することを言った $$$P + P$ 曲線の接線を $$$P$ 。 しかし、連続性がない場合、「接線」という言葉はすべての意味を失います。 この問題や他の問題を回避する方法を見つけることができますが、純粋に幾何学的な方法は複雑すぎて完全に非実用的です。



代わりに、 ポイントを追加するために作成した対話型ツールを試すことができます。

楕円曲線のグループ順序

有限体上に定義された楕円曲線は有限数の点を持っていると言いました。 重要な質問に答える必要があります。そこにはいくつのポイントがありますか？



最初に、グループ内のポイントの数をグループ順序と呼びます。



可能なすべての値を確認する $$$x$ 0からの範囲で $$$p-1$ ポイントをカウントすることは不可能な方法になります。 $$$O（p）$ 次の場合、このタスクは「難しい」 $$$p$ 大きな素数です。



幸いなことに、順序を計算するためのより高速なアルゴリズムがあります： Schoofのアルゴリズム 。 私はその詳細には立ち入りません-主なことは、それが多項式時間で行われることであり、これが我々が必要なことです。

スカラー乗算と巡回サブグループ

実数の場合、乗算は次のように定義できます。

$$

$$n P = \アンダーブレース{P + P + \ cdots + P} _ {n \ \ text {times}}$$

繰り返しになりますが、倍加アルゴリズムを使用して、乗算を実行できます。 $$$O（k）$ どこで $$$k$ ビット数です $$$n$ ） スカラー乗算のためのインタラクティブツールを書きました 。



楕円曲線上の点の乗算 $$$\ mathbb {F} _p$ 興味深い特性があります。 曲線を描く $$$y ^ 2 \ equiv x ^ 3 + 2x + 3 \ pmod {97}$ そしてポイント $$$P =（3、6）$ 。 ここで、次の倍数であるすべての値を計算します $$$P$ ：









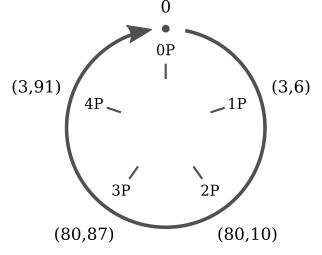
すべての値はの倍数です $$$P =（3、6）$ 5つの異なるポイント（ $$$0$ 、 $$$P$ 、 $$$2P$ 、 $$$3P$ 、 $$$4P$ ）周期的に繰り返されます。 楕円曲線のスカラー乗算とモジュラー演算の加算の類似性に気付くのは簡単です。

• $$$0P = 0$
• $$$1P =（3、6）$
• $$$2P =（80、10）$
• $$$3P =（80、87）$
• $$$4P =（3、91）$
• $$$5P = 0$
• $$$6P =（3、6）$
• $$$7P =（80、10）$
• $$
• $$$9P =（3、91）$
• ...

すぐに2つの機能に気付くことができます。まず、値の倍数の値 $$$P$ 、5つのみ：楕円曲線の他の点は決してそれらになりません。 第二に、それらは周期的に繰り返されます。 あなたは書くことができます：

• $$$5kP = 0$
• $$$（5k + 1）P = P$
• $$$（5k + 2）P = 2P$
• $$$（5k + 3）P = 3P$
• $$$（5k + 4）P = 4P$

全体として $$$k$ 。 剰余除算演算子のおかげで、これらの5つの方程式は1つに「絞る」ことができます。 $$$kP =（k \ bmod {5}）P$ 。



さらに、 これらの5つのポイントが加算操作に関して閉じていることをすぐに示すことができます 。 それはどういう意味ですか：要約しても $$$0$ 、 $$$P$ 、 $$$2P$ 、 $$$3P$ または $$$4P$ 、結果は常にこれら5つのポイントのいずれかになります。 繰り返しますが、楕円曲線の他のすべての点が結果になることはありません。



同じことが他のすべてのポイントにも当てはまります。 $$$P =（3、6）$ 。 実際、私たちが取れば $$$P$ 一般的な形式では：

$$

$$nP + mP = \下括弧{P + \ cdots + P} _ {n \ \ text {times}} + \下括弧{P + \ cdots + P} _ {m \ \ text {times}} =（n + m）P$$

つまり：の倍数である2つの値を追加すると $$$P$ 、その後、 $$$P$ （つまり、値の倍数である値 $$$P$ 加算操作に関して閉じられています）。 これは、複数のセットが $$$P$ 値は 、楕円曲線によって形成されるグループの循環サブグループです 。



「サブグループ」は、別のグループのサブセットであるグループです。 「循環サブグループ」は、前の例で示したように、要素が循環的に繰り返されるサブグループです。 ポイント $$$P$ 循環サブグループのジェネレータまたはベースポイントと呼ばれます。



サイクリックサブグループは、ECCおよびその他の暗号システムの基盤です。 後でこれがなぜそうなのかを説明します。

サブグループ注文

ポイントによって生成されたサブグループの順序は何だろうと思うかもしれません $$$P$ （または、言い換えれば、順序は何ですか $$$P$ ） この質問に答えるためにSchoofアルゴリズムを使用することはできません。このアルゴリズムは楕円曲線全体に対してのみ機能し、サブグループには機能しないためです。 問題の解決に進む前に、さらに情報が必要です。

• これまで、順序をグループ内のポイントの数として定義しました。 この定義はまだ有効ですが、循環サブグループでは、新しい同様の定義を指定できます。 $$$P$ 最小の正の整数です $$$n$ そのような $$$nP = 0$ 。
  
  
  
  実際、前の例を見ると、サブグループは5つのポイントで構成されており、 $$$5P = 0$ 。
• ご注文 $$$P$ ラグランジュ定理による楕円曲線の次数に接続されています。これに応じて、サブグループの次数は元のグループの次数の約数です 。
  
  
  
  言い換えれば、楕円曲線が $$$N$ ポイント、およびサブグループの1つに含まれる $$$n$ それから $$$n$ 仕切りです $$$N$ 。

これらの2つの事実により、基点を持つサブグループの順序を決定する機会が得られます。 $$$P$ ：

1. 楕円曲線の次数を計算する $$$N$ Schufアルゴリズムを使用します。
2. すべての仕切りを見つける $$$N$ 。
3. 各除数について $$$n$ 秩序の $$$N$ 計算する $$$nP$ 。
4. 最小 $$$n$ そのような $$$nP = 0$ は、サブグループの順序です。

たとえば、曲線 $$$y ^ 2 = x ^ 3-x + 3$ フィールド上 $$$\ mathbb {F} _ {37}$ 順序があります $$$N = 42$ 。 そのサブグループは秩序があるかもしれません $$$n = 1$ 、 $$$2$ 、 $$$3$ 、 $$$6$ 、 $$$7$ 、 $$$14$ 、 $$$21$ または $$$42$ 。 代用すれば $$$P =（2、3）$ それから私たちはそれを見るでしょう $$$P \ ne 0$ 、 $$$2P \ ne 0$ 、...、 $$$7P = 0$ つまり、順序 $$$P$ 等しい $$$n = 7$ 。



ランダムな除数ではなく、最小のものを取ることが重要であることを考慮してください。 ランダムに選択すると、取得できます $$$n = 14$ 、これはサブグループの順序ではなく、複数の順序の1つです。



別の例：方程式によって定義された楕円曲線 $$$y ^ 2 = x ^ 3-x + 1$ フィールド上 $$$\ mathbb {F} _ {29}$ 順序があります $$$N = 37$ 素数です。 そのサブグループは注文のみ可能です $$$n = 1$ または $$$37$ 。 推測できるように $$$n = 1$ 、サブグループには無限遠点のみが含まれます。 いつ $$$n = N$ 、サブグループには楕円曲線のすべての点が含まれます。

ベースポイント検索

ECCアルゴリズムには、高次のサブグループが必要です。 したがって、通常、楕円曲線が選択され、その次数が計算されます（ $$$N$ ）、グループの順序（ $$$n$ ）大きな除数が選択され、適切なベースポイントが見つかります。 つまり、基点を選択せず​​、その順序を計算した後、逆の操作を実行します。まず、かなり適切な順序を選択してから、適切な基点を探します。 これを行う方法？



最初に、別の概念を導入する必要があります。 ラグランジュの定理は、その数が $$$h = N / n$ 常に全体 （なぜなら $$$n$ -仕切り $$$N$ ） 数 $$$h$ それはそれ自身の名前を持っています：それはサブグループ補因子です。



ここで、楕円曲線の各点に対して、 $$$NP = 0$ 。 これは本当です $$$N$ 可能な倍数です $$$n$ 。 補因子の定義に基づいて、次のように記述できます。

$$

$$n（hP）= 0$$

今、それを仮定します $$$n$ -素数（記事の最初の部分で述べられている理由から、単純な注文を好む）。 この形式で書かれたこの方程式は、 $$$G = hP$ 順序のサブグループを作成します $$$n$ （除く $$$G = hP = 0$ サブグループの順序は1）です。



これに照らして、次のアルゴリズムを定義できます。

1. 注文を計算する $$$N$ 楕円曲線。
2. 注文を選択してください $$$n$ サブグループ。 アルゴリズムが機能するには、数値が素数で除数である必要があります $$$N$ 。
3. 補因子を計算する $$$h = N / n$ 。
4. 曲線上のランダムな点を選択します $$$P$ 。
5. 計算する $$$G = hP$ 。
6. もし $$$G$ 0に等しい場合、ステップ4に戻ります。それ以外の場合、次数を持つサブグループジェネレーターが見つかりました。 $$$n$ そして補因子 $$$h$ 。

アルゴリズムは次の場合にのみ機能することに注意してください。 $$$n$ シンプル。 場合のみ $$$n$ 注文は簡単ではなかった $$$G$ 仕切りの1つである可能性があります $$$n$ 。

離散対数

連続楕円曲線の場合と同様に、次の質問について議論する必要があります。 $$$P$ そして $$$Q$ それから何になります $$$k$ そのような $$$Q = kP$ ？



楕円曲線の離散対数問題として知られるこのタスクは、「複雑」であると見なされ、従来のコンピューターで実行されている多項式時間アルゴリズムは見つかりませんでした。 ただし、このビューには数学的証拠はありません。



このタスクは、デジタル署名アルゴリズム（DSA）、Diffie-Hellmanプロトコル（DH）、El-Gamalスキームなどの他の暗号システムで使用される離散対数問題に似ています。 タスクの名前は偶然一致しません。 それらの違いは、これらのアルゴリズムがスカラー乗算ではなく、累乗法を使用することです。 それらの離散対数問題は次のように定式化できます：既知の場合 $$$a$ そして $$$b$ それから何になります $$$k$ そのような $$$b = a ^ k \ bmod {p}$ ？



これらの問題は両方とも、有限集合（より具体的には循環サブグループ）を使用するため、「離散」です。 そして、それらは通常の対数に似ているため、「対数」です。



ECCは、現時点では、楕円曲線の離散対数問題が暗号化で使用される他の同様のタスクと比較して「より複雑」であるという点で興味深いです。 これは、全体として必要なビットが少ないことを意味します $$$k$ 他の暗号システムと同じレベルの保護を得るために、この記事の最後の第4部でこれを詳細に検討します。

パート3：ECDHおよびECDSA

スコープパラメーター

楕円曲線アルゴリズムは、有限体上の楕円曲線の循環サブグループで機能します。 したがって、アルゴリズムには次のパラメーターが必要です。

• シンプル $$$p$ 最終フィールドのサイズを定義します。
• オッズ $$$a$ そして $$$b$ 楕円曲線方程式。
• 基点 $$$G$ サブグループを生成します。
• ご注文 $$$n$ サブグループ。
• コファクター $$$h$ サブグループ。

その結果、アルゴリズムのドメインのパラメーターは6 $$$(p, a, b, G, n, h)$ 。

ランダム曲線

離散対数問題が「複雑」だと言ったとき、私は完全に正確ではありませんでした。かなり弱い楕円曲線のクラスがあり、特殊なアルゴリズムを使用して離散対数問題を効果的に解決できます。たとえば、$$$p = hn$（つまり、最終フィールドの次数は楕円曲線の次数に等しい）、スマート攻撃に対して脆弱です。これは、古典的なコンピューターで多項式時間の離散対数を解くために使用できます。



今、カーブ定義エリアのパラメータを与えたと仮定します。誰にも知られていない新しいクラスの弱い曲線を発見した可能性があり、おそらく、曲線の離散対数を計算するための「高速」アルゴリズムを作成しました。どうすればその反対、つまり 脆弱性について知らないのですか？曲線が「保護されている」ことをどのように保証できますか（自分の攻撃に使用できないという意味で）。



この問題を解決するには、定義エリアの追加パラメーターを使用する必要がある場合があります。シード値 $$$S$ 。 これは、係数の生成に使用される乱数です。 $$$a$ そして $$$b$ または基点 $$$G$または両方。これらのパラメーターは、ハッシュ計算によって生成されます。$$$S$ 。 ハッシュは、ご存じのとおり、計算は「簡単」ですが、元に戻すのは「困難」です。









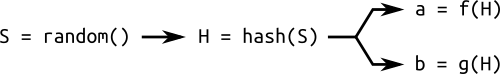
生成値からランダム曲線を生成するための単純なスキーム：乱数ハッシュを使用して、曲線のさまざまなパラメーターを計算します。









定義エリアのパラメーターからハッシュをチートして再作成したい場合、「困難な」問題を解決する必要があります：ハッシュを逆にする。



生成値を使用して生成された曲線は、ランダムにチェックと呼ばれます。ハッシュを使用してパラメータを生成する原理は、「私の袖に何もない」として知られており、暗号化で広く使用されています。



このトリックは、作者に知られている脆弱性を持つような方法で曲線が特別に作成されなかったという特定の保証を与えます。実際、生成値と一緒に曲線を与えると、パラメーターをarbitrarily意的に選択できなかったことを意味します$$$a$ そして $$$b$、そしてあなたは私が特別な攻撃を使用できないことを比較的冷静にすることができます。「相対」という言葉を使用する理由については、第4部で説明します。



ランダム曲線を生成およびチェックするための標準化されたアルゴリズムは、ANSI X9.62で説明されており、SHA-1に基づいています。興味がある場合は、SECG仕様でテスト可能なランダム曲線を生成するためのアルゴリズムについて読むことができます（「検証可能なランダム曲線とベースポイントジェネレーター」を参照）。OpenSSLに同梱されているすべてのランダム曲線をチェック



する小さなPythonスクリプトを作成しました。私はそれを見ることを強くお勧めします！

楕円曲線暗号

私たちは多くの時間を費やしましたが、ついにそこに着きました！簡単です：

1. 秘密鍵はランダムな整数です$$$d$ から選択 $$$\{1, \dots, n - 1\}$ （どこ $$$n$ -サブグループの順序）。
2. 公開鍵がポイントです$$$H = dG$ （どこ $$$G$ -サブグループの基点）。

ほら 知っていれば$$$d$ そして $$$G$ （定義ドメインの他のパラメーターと一緒に）、次に見つけます $$$H$「シンプル。」しかし、私たちが知っていれば$$$H$ そして $$$G$、秘密鍵を検索 $$$d$ 離散対数問題を解く必要があるため、「難しい」問題です。



次に、この原理に基づいた2つの公開キーアルゴリズムについて説明します：暗号化に使用されるECDH（楕円曲線の楕円曲線Diffie-Hellman、Diffie-Hellmanプロトコル）、およびデジタル署名に使用されるECDSA（楕円曲線デジタル署名アルゴリズム）。

ECDHを使用した暗号化

ECDHは、楕円曲線用のDiffie-Hellmanアルゴリズムのバリエーションです。実際、暗号化アルゴリズムではなく、鍵合意プロトコルである可能性が高くなります。本質的に、これはECDHがキーを生成および交換する順序を（ある程度まで）定義することを意味します。このようなキーを使用して、データを暗号化する方法を自分で選択できます。



次の問題を解決します。2者（通常はAliceとBob）は、第三者（仲介者、Man In the Middle）が情報を傍受できるが解読できないように、情報を安全に交換したい。たとえば、これはTLSの原則の1つです。



仕組みは次のとおりです。

1. まず、アリスとボブは、自分の秘密鍵と公開鍵を生成します。アリスには秘密鍵があります$$$d_A$ および公開鍵 $$$H_A = d_AG$ ボブには鍵があります $$$d_B$ そして $$$H_B = d_BG$ 。 アリスとボブの両方が同じ定義領域パラメーターを使用することに注意してください：1つのベースポイント $$$G$ 同じ有限体の1つの楕円曲線上。
2. アリスとボブは公開鍵を交換します $$$H_A$ そして $$$H_B$ 保護されていないチャネルを通じて。仲介（中間者）傍受$$$H_A$ そして $$$H_B$ しかし、どちらも識別できません $$$d_A$ また $$$d_B$ 離散対数問題を解くことなく。
3. アリス計算 $$$S = d_A H_B$ （ボブ自身の秘密鍵とボブの公開鍵を使用）、ボブは計算します $$$S = d_B H_A$ （アリス自身の秘密鍵とアリスの公開鍵を使用）。に注意してください$$$S$アリスとボブの両方で同じです。実際には：
   
   
   
   
   
   
   
   
   

   $$

   $$S = d_A H_B = d_A (d_B G) = d_B (d_A G) = d_B H_A$$
   
   
   
   
   

ただし、仲介者は $$$H_A$ そして $$$H_B$（定義ドメインの他のパラメータと一緒に）、彼は共有秘密鍵を見つけることができなくなります $$$S$ 。 これはDiffie-Hellman問題と呼ばれ、次のように定式化できます。

結果はどうなりますか $$$abP$ 3点 $$$P$ 、 $$$aP$ そして $$$bP$ ？

または同様に：

結果はどうなりますか $$$k^{xy}$ 3つの全体のために $$$k$ 、 $$$k^x$ そして $$$k^y$ ？

（後者の定式化は、モジュラー演算に基づいた元のDiffie-Hellmanアルゴリズムで使用されます。）









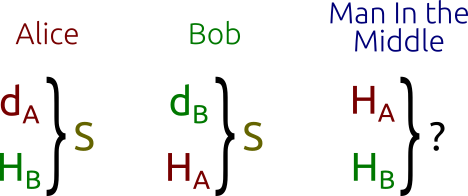
Diffie-Hellmanプロトコル：アリスとボブは共有秘密キーを「単純に」計算できますが、仲介者は「困難な」問題を解決する必要があります。



Diffie-Hellman問題の根底にある原理は、YouTubeの優れたKhan Academyビデオでも説明されています。このビデオでは、後でモジュラー演算（楕円曲線ではない）に適用されるDiffie-Hellmanアルゴリズムについて説明しています。



楕円曲線のDiffie-Hellman問題は「複雑」と見なされます。離散対数問題と同じくらい「複雑」であると考えられていますが、これについての数学的証拠はありません。対数問題を解くことはDiffie-Hellman問題を解く方法であるため、「難しく」なることはできないと自信を持って言うことができます。



共有秘密キーを受け取ったアリスとボブは、対称暗号化でデータを交換できます。



たとえば、座標を使用できます$$$x$ キー $$$S$AESや3DESなどの安全な暗号でメッセージを暗号化するためのキーとして。これがTLSの機能です。違いは、TLSが座標を接続することです$$$x$ 接続に関連する他の数値を使用して、結果のバイト文字列のハッシュを計算します。

ECDH実験

私は楕円曲線上で秘密/公開鍵と共有秘密鍵を計算する別のPythonスクリプトを書きました。



前述の例とは異なり、このスクリプトでは、小さなフィールドの単純な曲線ではなく、標準化された曲線を使用します。私はカーブ選んだsecp256k1



グループSECG（ベース、«効率的な暗号化グループのための規格です» のCerticom）。同じ曲線がビット署名でデジタル署名に使用されます。スコープのオプションは次のとおりです。

• $$$p$ = 0xffffffff ffffffff ffffffff ffffffff ffffffff ffffffff fffffffe fffffc2f
• $$$a$ = 0
• $$$b$ = 7
• $$$x_G$ = 0x79be667e f9dcbbac 55a06295 ce870b07 029bfcdb 2dce28d9 59f2815b 16f81798
• $$$y_G$ = 0x483ada77 26a3c465 5da4fbfc 0e1108a8 fd17b448 a6855419 9c47d08f fb10d4b8
• $$$n$ = 0xffffffff ffffffff ffffffff fffffffe baaedce6 af48a03b bfd25e8c d0364141
• $$$h$ = 1

（これらの番号はOpenSSLソースコードから取得されます。）



もちろん、スクリプトを変更し、定義領域の他の曲線とパラメーターを使用できます。単純なフィールドと通常のWeierstrass定式を使用してください。そうしないと、スクリプトは機能しません。



このスクリプトは非常にシンプルで、上記のアルゴリズムの一部（ポイントの追加、倍加、ECDH）が含まれています。勉強して実行することをお勧めします。およそ次の出力が作成されます。

 Curve: secp256k1 Alice's private key: 0xe32868331fa8ef0138de0de85478346aec5e3912b6029ae71691c384237a3eeb Alice's public key: (0x86b1aa5120f079594348c67647679e7ac4c365b2c01330db782b0ba611c1d677, 0x5f4376a23eed633657a90f385ba21068ed7e29859a7fab09e953cc5b3e89beba) Bob's private key: 0xcef147652aa90162e1fff9cf07f2605ea05529ca215a04350a98ecc24aa34342 Bob's public key: (0x4034127647bb7fdab7f1526c7d10be8b28174e2bba35b06ffd8a26fc2c20134a, 0x9e773199edc1ea792b150270ea3317689286c9fe239dd5b9c5cfd9e81b4b632) Shared secret: (0x3e2ffbc3aa8a2836c1689e55cd169ba638b58a3a18803fcf7de153525b28c3cd, 0x43ca148c92af58ebdb525542488a4fe6397809200fe8c61b41a105449507083)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

エフェメラルECDH

ECDHではなくECDHEについて聞いたことがある人もいるかもしれません。ECHDEの「E」は「Ephemeral」（一時）を表し、送信されたキーが一時的であり、静的ではないという事実によるものです。



ECDHEは、たとえば、TLSで使用されます。TLSでは、接続を確立するときに、クライアントとサーバーがその場で秘密/公開キーペアを生成します。次に、鍵はTLS証明書（承認用）で署名され、当事者間で転送されます。

ECDSAで署名する

シナリオは次のとおりです。アリスは自分の秘密鍵（$$$d_A$）、ボブはアリスの公開鍵で署名を検証したい（$$$H_A$ ）アリス以外は有効な署名を作成できないはずです。誰もが署名を検証できるはずです。



アリスとボブは再び同じスコープパラメーターを使用します。楕円曲線に適用されるデジタル署名アルゴリズムの一種であるECDSAアルゴリズムを見ていきます。



ECDSAは、メッセージ自体ではなく、メッセージハッシュで機能します。ハッシュ関数の選択は残りますが、明らかに、暗号化ハッシュ関数を選択する必要があります。ハッシュビット長がビット長と同じになるように、メッセージハッシュを切り捨てる必要があります$$$n$（サブグループの順序）。切り捨てられたハッシュは整数であり、次のように示されます $$$z$ 。



アリスがメッセージに署名するために実行するアルゴリズムは、次のように機能します。

1. ランダムな整数を取る $$$k$ から選択 $$$\{1, \dots, n - 1\}$ （どこ $$$n$ -これはまだグループの順序です）。
2. ポイントを計算する $$$P = kG$ （どこ $$$G$ -サブグループの基点）。
3. 数を計算します $$$r = x_P \bmod{n}$ （どこ $$$x_P$ 座標です $$$x$$$$P$ ）
4. もし $$$r = 0$ 、別のものを選択 $$$k$ もう一度やり直してください。
5. 計算する $$$s = k^{-1} (z + rd_A) \bmod{n}$ （どこ $$$d_A$ -アリスの秘密鍵、および $$$k^{-1}$ -乗法反転 $$$k$ モジュロ $$$n$ ）
6. もし $$$s = 0$ 、別のものを選択 $$$k$ もう一度やり直してください。

夫婦 $$$(r, s)$ は署名です。









アリスはハッシュに署名します $$$z$ 秘密鍵を使用する $$$d_A$ そしてランダム $$$k$ 。 ボブはアリスの公開鍵を使用してメッセージの署名を検証します $$$H_A$ 。



簡単に言えば、このアルゴリズムは最初に秘密鍵（ $$$k$ ） ポイントの乗算のおかげで（これは、私たちが知っているように、一方向は「単純」で、反対方向は「複雑」です）、秘密鍵は $$$r$ 。 それから $$$r$ 方程式によってメッセージハッシュに添付 $$$s = k^{-1} (z + rd_A) \bmod{n}$ 。



計算することに注意してください $$$s$ 逆数を計算しました $$$k$ モジュロ $$$n$ 。 前の部分で述べたように、これは次の場合にのみ機能することが保証されています。 $$$n$ 素数です。 サブグループが複素数のオーダーである場合、ECDSAは使用できません。すべての標準化された曲線が単純な順序を持っていることは偶然ではなく、困難な順序を持つことはECDSAに適用されません。

署名検証

署名を検証するには、アリスの公開鍵が必要です $$$H_A$ 、（切り捨てられた）ハッシュ $$$z$ そして明らかに署名 $$$(r, s)$ 。

1. 整数を計算します $$$u_1 = s^{-1} z \bmod{n}$ 。
2. 整数を計算します $$$u_2 = s^{-1} r \bmod{n}$ 。
3. ポイントを計算する $$$P = u_1 G + u_2 H_A$ 。

署名は次の場合にのみ有効です $$$r = x_P \bmod{n}$ 。

アルゴリズムの正確さ

一見、アルゴリズムのロジックは明らかではないかもしれませんが、以前に書き留めたすべての方程式を組み合わせると、すべてが明確になります。



で始まる$$$P = u_1 G + u_2 H_A$ 。 公開鍵の定義から、私たちはそれを知っています $$$H_A = d_A G$ （どこ $$$d_A$-秘密鍵）。あなたは書くことができます：

$$

$$\begin{array}{rl} P & = u_1 G + u_2 H_A \\ & = u_1 G + u_2 d_A G \\ & = (u_1 + u_2 d_A) G \end{array}$$

定義の対象 $$$u_1$ そして $$$u_2$ 書くことができます：

$$

$$\begin{array}{rl} P & = (u_1 + u_2 d_A) G \\ & = (s^{-1} z + s^{-1} r d_A) G \\ & = s^{-1} (z + r d_A) G \end{array}$$

ここでは、「 $$$\text{mod}\ n$ "、簡潔さと、ポイントによって生成された循環サブグループ $$$G$ 順序があります $$$n$ 、つまり、 $$$\text{mod}\ n$「冗長。



以前に決定した$$$s = k^{-1} (z + rd_A) \bmod{n}$ 。 方程式の両側に乗算する $$$k$ そして、除算 $$$s$ 私達は得る： $$$k = s^{-1} (z + rd_A) \bmod{n}$ 。 この結果を次の方程式に代入します $$$P$ 私達は得る：

$$

$$\begin{array}{rl} P & = s^{-1} (z + r d_A) G \\ & = k G \end{array}$$

これは同じ方程式です。 $$$P$ 署名生成アルゴリズムのステップ2で取得したものです！署名を生成してチェックするとき、同じポイントを計算します$$$P$、ちょうど異なる方程式のセット。これがアルゴリズムが機能する理由です。

ECDSAの実験

もちろん、署名を生成および検証するPythonスクリプトを作成しました。コードは、ECDHスクリプトの一部、特に定義領域のパラメーターと秘密/公開キーペアを生成するアルゴリズムをコピーします。



このスクリプトによって生成される出力は次のとおりです。

 Curve: secp256k1 Private key: 0x9f4c9eb899bd86e0e83ecca659602a15b2edb648e2ae4ee4a256b17bb29a1a1e Public key: (0xabd9791437093d377ca25ea974ddc099eafa3d97c7250d2ea32af6a1556f92a, 0x3fe60f6150b6d87ae8d64b78199b13f26977407c801f233288c97ddc4acca326) Message: b'Hello!' Signature: (0xddcb8b5abfe46902f2ac54ab9cd5cf205e359c03fdf66ead1130826f79d45478, 0x551a5b2cd8465db43254df998ba577cb28e1ee73c5530430395e4fba96610151) Verification: signature matches Message: b'Hi there!' Verification: invalid signature Message: b'Hello!' Public key: (0xc40572bb38dec72b82b3efb1efc8552588b8774149a32e546fb703021cf3b78a, 0x8c6e5c5a9c1ea4cad778072fe955ed1c6a2a92f516f02cab57e0ba7d0765f8bb) Verification: invalid signature
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ご覧のとおり、スクリプトは最初にメッセージ（バイト文字列「Hello！」）に署名し、次に署名をチェックします。次に、彼は別のメッセージの同じ署名を検証しようとします（ "こんにちは！"）検証は失敗します。最後に、彼は正しいメッセージの署名の検証を検証しようとしますが、別のランダムな公開鍵を使用して、検証も失敗します。

重要度k

ECDSA署名を生成するときは、秘密にしておくことが重要です $$$k$本当に秘密。使用した場合$$$k$すべての署名または乱数ジェネレーターがある程度予測可能であれば、攻撃者は秘密鍵を決定できます！



ソニーは数年前に同様の間違いを犯しました。PlayStation 3ゲームコンソールでは、ECDSAアルゴリズムを使用してSonyによって署名されたゲームのみを実行できました。つまり、PlayStation 3用の新しいゲームを作成する場合、Sonyの署名がないユーザーに配布することはできません。問題は、Sonyによって作成されたすべての署名が静的を使用して生成されたことでした$$$k$ 。



（これは、乱数ジェネレータの作成者が、ソニーに触発されたものと思わXKCD、またはディルバート。）



このような状況で、あなたは簡単に秘密鍵を回復することができます$$$d_S$ ソニーは、署名済みのゲームを2つだけ購入した後、ハッシュを抽出します（ $$$z_1$ そして $$$z_2$ ）および署名（ $$$(r_1, s_1)$ そして $$$(r_2, s_2)$ ）ドメインのパラメータと一緒に。 これは次のように行われます。

• まず、それを考慮する必要があります $$$r_1 = r_2$ （なぜなら $$$r = x_P \bmod{n}$ そして $$$P = kG$ 両方の署名で同じ）。
• 受け入れる $$$(s_1 - s_2) \bmod{n} = k^{-1} (z_1 - z_2) \bmod{n}$ （この結果は、 $$$s$ ）
• 方程式の両側に乗算する $$$k$ ： $$$k (s_1 - s_2) \bmod{n} = (z_1 - z_2) \bmod{n}$ 。
• で割った $$$(s_1 - s_2)$ 取得する $$$k = (z_1 - z_2)(s_1 - s_2)^{-1} \bmod{n}$ 。

最後の方程式により、計算することができます $$$k$ハッシュとそれに対応する署名が2つだけです。今の方程式を使用して$$$s$ 秘密鍵を取得できます。

$$

$$s = k^{-1}(z + rd_S) \bmod{n}\ \ \Rightarrow\ \ d_S = r^{-1} (sk - z) \bmod{n}$$

同様の手法は次の場合に適用できます。 $$$k$ 静的ではありませんが、何らかの形で予測可能です。

パート4：ECC保護をハッキングするためのアルゴリズムとRSAとの比較

前のパートでは、2つのアルゴリズム（ECDHとECDSA）を調べ、楕円曲線の離散対数問題がその安全性に重要な役割を果たす理由を見つけました。しかし、覚えているなら、離散対数問題の複雑さの数学的証明はないと言った。それは「複雑」であると信じているが、それについては確信がない。記事の最初の部分では、現代の技術で実際にどれだけ「難しい」かを評価しようとしました。



第二部では、RSA（およびモジュラー演算に基づく他の暗号システム）がうまく機能する場合、なぜ楕円曲線の暗号化が必要なのかという質問に答えようとしました。

離散対数のハッキング

次に、楕円曲線上の離散アルゴリズムを計算するための最も効率的な2つのアルゴリズム、ベイビーステップアルゴリズム、ジャイアントステップアルゴリズム、およびポラードρアルゴリズムを検討します。



開始する前に、離散対数問題が何であるかを思い出します。2つの与えられた点を見つける $$$P$ そして $$$Q$ 整数 $$$x$ 方程式を満たす $$$Q = xP$ 。 点は、基点を持つ楕円曲線のサブグループに属します $$$G$ そして注文 $$$n$ 。

ベビーステップ、ジャイアントステップ

まず、簡単な議論をします。いつでもすべてを書き留めることができます $$$x$ どうやって $$$x = am + b$ どこで $$$a$ 、 $$$m$ そして $$$b$-3つの任意の整数。たとえば、次のように書くことができます$$$10 = 2 \cdot 3 + 4$ 。



これを念頭に置いて、離散対数問題の方程式を次のように書き換えることができます。

$$

$$\begin{array}{rl} Q & = xP \\ Q & = (am + b) P \\ Q & = am P + b P \\ Q - am P & = b P \end{array}$$

ベビーステップジャイアントステップは、「中間会議」アルゴリズムです。総当たり攻撃（すべてのポイントを計算する必要がある）とは異なり$$$xP$ それぞれについて $$$x$ 見つけるまで $$$Q$ ）、「複数の」値を計算することが可能です $$$bP$ および「いくつかの」値 $$$Q - amP$一致が見つかるまで。アルゴリズムは次のように機能します。

1. 計算する $$$m = \left\lceil{\sqrt{n}}\right\rceil$
2. それぞれについて $$$b$ から $$${0, \dots, m}$ 計算する $$$bP$ 結果をハッシュテーブルに保存します。
3. それぞれについて $$$a$ から $$${0, \dots, m}$ ：
   1. 計算する $$$amP$ ;
   2. 計算する $$$Q - amP$ ;
   3. ハッシュテーブルをチェックしてポイントを探す $$$bP$ そのような $$$Q - amP = bP$ ;
   4. そのような点が存在する場合、私たちは見つけました $$$x = am + b$ 。

ご覧のとおり、最初にポイントを計算します $$$bP$係数の小さな増分（「ベビーステップ」）$$$b$ （ $$$1P$ 、 $$$2P$ 、 $$$3P$、...）。アルゴリズムの2番目の部分では、ポイントを計算します$$$amP$大きな増分（「ジャイアントステップ」「ジャイアントステップ」）で$$$am$ （ $$$1mP$ 、 $$$2mP$ 、 $$$3mP$ 、... $$$m$ -多数）。









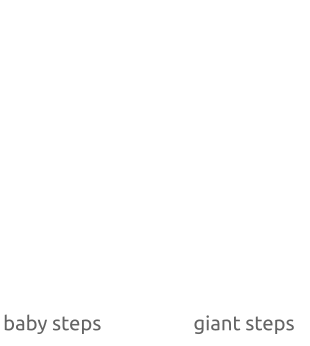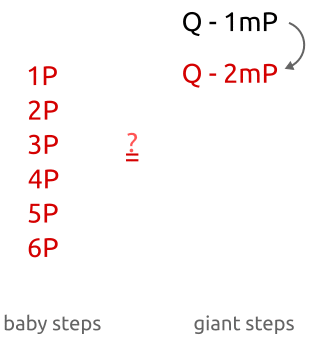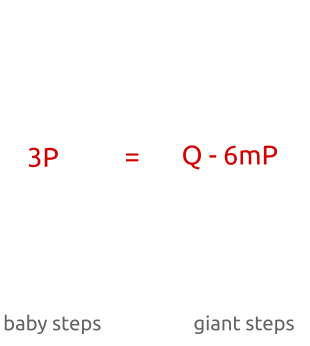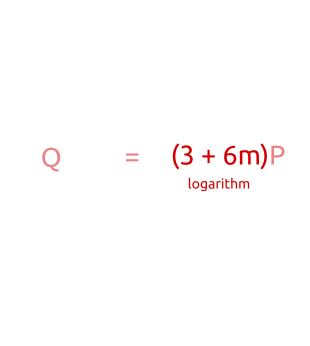
ベビーステップ、ジャイアントステップアルゴリズム：最初に、小さなステップでいくつかのポイントを計算し、それらをハッシュテーブルに保存します。次に、大きなステップを実行して、新しいポイントをハッシュテーブル内のポイントと比較します。対応が見つかったら、項の単純な順列により離散アルゴリズムを計算できます。



アルゴリズムがどのように機能するかを理解するために、しばらくの間、$$$bP$ キャッシュされ、方程式を取ります $$$Q = amP + bP$ 。 これから次のことを考慮してください。

• で $$$a = 0$ 私たちはチェックします $$$Q$ 数 $$$bP$ どこで $$$b$ -0〜0の整数のいずれか $$$m$ 。 だから私たちは比較します $$$Q$ すべてのポイントから $$$0P$ 前に $$$mP$ 。
• で $$$a = 1$ 私たちはチェックします $$$Q$ 数 $$$mP + bP$ 。 比較する $$$Q$ すべてのポイントから $$$mP$ 前に $$$2mP$ 。
• で $$$a = 2$ 私たちは比較します $$$Q$ すべてのポイントから $$$2mP$ 前に $$$3mP$ 。
• ...
• で $$$a = m - 1$ 私たちは比較します $$$Q$ すべてのポイントから $$$(m - 1)mP$ 前に $$$m^2 P = nP$ 。

その結果、すべてのポイントをチェックしました $$$0P$ 前に $$$nP$ （つまり、可能なすべてのポイント）これ以上完了することにより $$$2m$ 加算と乗算（正確に$$$m$ 「子供の歩み」のために、もう $$$m$「ジャイアントステップ」の場合）。



ハッシュテーブルの検索に時間がかかると仮定する$$$O(1)$このアルゴリズムには時間的および空間的な複雑性があることが簡単にわかります $$$O(\sqrt{n})$ （または $$$O(2^{k / 2})$ ビット長を考慮して）。これはまだ指数関数的な時間ですが、ブルートフォース攻撃よりもはるかに優れています。

実際のベビーステップのジャイアントステップ

複雑さの意味を理解することは理にかなっています。 $$$O(\sqrt{n})$実際に。標準化された曲線を取ります：prime192v1



（she secp192r1



、ansiX9p192r1



）。この曲線は秩序です$$$n$= 0xffffffff ffffffff ffffffff 99def836 146bc9b1 b4d22831。の平方根$$$n$-これは約7.922816251426434・10 ²⁸（ほぼ80オクティリオン [約Transl .:短いスケールで]）です。



格納するものを想像してください$$$\sqrt{n}$ハッシュテーブル内のポイント。各ポイントが正確に32バイトを占有するとします。ハッシュテーブルには約2.5・10 ³⁰バイトのメモリが必要です。インターネットを検索すると、世界中のドライブの現在の合計容量がゼタバイト（10 ²¹バイト）程度であることがわかります。これは、ハッシュテーブルに必要なメモリ量よりもほぼ10桁少ないです！ポイントがそれぞれ1バイトを占めていたとしても、すべてを保存することはできませんでした。



これは印象的であり、覚えているならさらに印象的ですprime192v1



-これは最小次数を持つ曲線の1つです。secp521r1



（別の標準NIST曲線の）次数は約6.9・10 ¹⁵⁶です！

ベビーステップジャイアントステップの実験

私が書いたのPythonにスクリプトをアルゴリズムベビーステップジャイアント・ステップを使用して、離散対数を計算し、。明らかに、これは小さな次数の曲線でのみ機能しsecp521r1



ますMemoryError



。取得したい場合を除き、使用しないでください。



スクリプトは、およそ次の出力を生成します。

 Curve: y^2 = (x^3 + 1x - 1) mod 10177 Curve order: 10331 p = (0x1, 0x1) q = (0x1a28, 0x8fb) 325 * p = q log(p, q) = 325 Took 105 steps
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ρポラード

ρポラードは、離散対数を計算するための別のアルゴリズムです。同じ漸近的な時間の複雑さを持ちます。$$$O(\sqrt{n})$ ベビーステップのジャイアントステップですが、その空間的な複雑さは $$$O(1)$ 。巨大なメモリ要件のために、ベビーステップジャイアントステップが離散対数を解決できなかった場合、ρポラードはそれを処理できますか？確認しましょう...



最初に、離散対数問題をもう一度思い出させてください：find for given$$$P$ そして $$$Q$ 全体 $$$x$ そのような $$$Q = xP$ 。 ポラードρアルゴリズムでは、わずかに異なる問題を解決します。 $$$P$ そして $$$Q$ 全体 $$$a$ 、 $$$b$ 、 $$$A$ そして $$$B$ そのような $$$aP + bQ = AP + BQ$ 。



4つの整数が見つかったら、次の方程式を使用できます。 $$$Q = xP$ 計算する $$$x$ ：

$$

$$\begin{array}{rl} aP + bQ & = AP + BQ \\ aP + bxP & = AP + BxP \\ (a + bx) P & = (A + Bx) P \\ (a - A) P & = (B - b) xP \end{array}$$

今、私たちは取り除くことができます $$$P$ 。 しかし、これを行う前に、サブグループが周期的であり、順序があることを忘れないでください $$$n$ 、つまり、ポイントの乗算に使用される係数はモジュロで取得されます $$$n$ ：

$$

$$\begin{array}{rl} a - A & \equiv (B - b) x \pmod{n} \\ x & = (a - A)(B - b)^{-1} \bmod{n} \end{array}$$

Oll Pollardの操作原理は単純です。ペアの擬似ランダムシーケンスを定義します $$$(a, b)$ 。 このペアのシーケンスを使用して、ポイントのシーケンスを生成できます。 $$$aP + bQ$ 。 以来 $$$P$ そして $$$Q$1つの循環サブグループの要素、点のシーケンス $$$aP + bQ$ また、周期的。



これは、ペアの擬似ランダムシーケンスを回る場合$$$(a, b)$遅かれ早かれ、サイクルが見つかります。つまり、ペアが見つかります $$$(a, b)$ そして別のペア $$$(A, B)$ そのような $$$aP + bQ = AP + BQ$ 。同じポイント、別々のペア：上記の方程式を適用して対数を見つけることができます。



課題は、効率的な方法でループを検出する方法ですか？

カメとウサギ

ループを検出するために、すべての可能な値を確認できます $$$a$ そして $$$b$ペア変換関数を使用しますが、$$$n^2$ そのようなペア、アルゴリズムは複雑になります $$$O（n ^ 2）$、これは単純な総当たり攻撃よりもはるかに悪いです。



しかし、より高速な方法があります：タートルアンドウサギアルゴリズム（フロイドサイクル検索アルゴリズムとも呼ばれます）。下の図は、ポラードρアルゴリズムの基になっているカメとウサギの方法の動作原理を示しています。









曲線があります $$$y^2 \equiv x^3 + 2x + 3 \pmod{97}$ とポイント $$$P = (3, 6)$ そして $$$Q = (80, 87)$ 。 ポイントは5次の循環サブグループに属します。2つの異なるペアが見つかるまで、異なる速度のペアのシーケンスを巡回します。 $$$(a, b)$ そして $$$(A, B)$ ワンポイントを与えます。この場合、ペアが見つかりました $$$(3, 3)$ そして $$$(2, 0)$ 、対数を次のように計算できます $$$x = (3 - 2)(0 - 3)^{-1} \bmod{5} = 3$ 。 そして実際、私たちはそれをやった $$$Q = 3P$ 。



本質的には、ペアの擬似ランダムシーケンスを使用します $$$(a, b)$ 対応するポイントのシーケンスとともに $$$aP + bQ$ 。 ペアのシーケンス $$$(a, b)$ 循環する場合もしない場合もありますが、ポイントのシーケンスは正確に循環します。 $$$P$ そして $$$Q$1つの基点から生成され、サブグループのプロパティから、スカラーの乗算と加算によってのみサブグループから「エスケープ」できないことがわかります。



次に、カメとウサギの2匹の動物を取り、左から右に順番に回します。カメ（画像の緑色の点）は遅く、各点を次々に読み取ります。ノウサギ（赤い点）は速く、すべてのステップで点をスキップします。



しばらくすると、カメとノウサギは1つのポイントを見つけますが、係数のペアは異なります。または、方程式に入れるために、カメはペアを見つけます$$$(a, b)$ ウサギはカップルです $$$(A, B)$ そのような $$$aP + bQ = AP + BQ$ 。



ランダムシーケンスがアルゴリズムを介して（静的に格納されていない）決定された場合、操作の原則にはすべてが必要であることが簡単にわかります。 $$$O(\log n)$ スペース。漸近時間の複雑さの計算はそれほど単純ではありませんが、時間の複雑さを示す確率的証明を構築できます $$$O(\sqrt{n}$ ）、私たちが言ったように。

ρポラードの実験

Pollardρアルゴリズムを使用して離散対数を計算するPythonスクリプトを作成しました。これは初期のρPollardの実装ではなく、そのわずかなバリエーションです（より効率的な方法でペアの擬似ランダムシーケンスを生成しました）。スクリプトには便利なコメントがありますので、アルゴリズムの詳細に興味がある場合は読んでください。



このスクリプトは、ベビーステップジャイアントステップと同様に、小さな曲線に対して機能し、同じ出力を生成します。

ロ・ポラードの実践

巨大なメモリ要件のため、ベビーステップのジャイアントステップは実際には使用できないと述べました。一方、Pollardのroアルゴリズムは、ほとんどメモリを必要としません。どのくらい実用的ですか？



1998年に、Certicomはビット長が109〜369の楕円曲線の離散対数を計算するための競争を開始しました。現在まで、109ビットのみが正常に解読されています。最後に成功した試みは2004年に行われました。ウィキペディアを引用するには：

この賞は2004年4月8日に、クリスモニコを代表とする約2,600人に授与されました。また、ポラードの一種の並列化されたroアルゴリズムも使用しました。この計算には17か月のカレンダー時間がかかりました。

先ほど言ったように、prime192v1



これは「最小の」楕円曲線の1つです。また、ρポラードには一時的な複雑さがあります$$$O(\sqrt{n})$ 。Chris Monikoと同じ手法（同じアルゴリズム、同じ機器、マシン数）を使用した場合、対数を計算するのにどれくらい時間がかかりprime192v1



ますか？

$$

$$17\ \text{}\ \times \frac{\sqrt{2^{192}}}{\sqrt{2^{109}}} \approx 5 \cdot 10^{13}\ \text{}$$

得られた結果はそれ自体を物語っており、そのような技術を使用して離散対数を解読することがいかに難しいかを明確にします。

ρポラードとベイビーステップジャイアントステップの比較

私が結合することを決めたスクリプトステップの赤ちゃんステップの巨人、ポラードROスクリプトおよび無効化スクリプトを中に第四スクリプト彼らのパフォーマンスを比較します。



この4番目のスクリプトは、異なるアルゴリズムを使用して「小さな」曲線上のすべてのポイントのすべての対数を計算し、それがかかった時間を報告します。

 Curve order: 10331 Using bruteforce Computing all logarithms: 100.00% done Took 2m 31s (5193 steps on average) Using babygiantstep Computing all logarithms: 100.00% done Took 0m 6s (152 steps on average) Using pollardsrho Computing all logarithms: 100.00% done Took 0m 21s (138 steps on average)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ご想像のとおり、列挙方法は他の2つに比べて非常に遅いです。ベビーステップジャイアントステップはより高速であり、ポラードのroアルゴリズムは、ベビーステップジャイアントステップよりも3倍以上遅くなります（ただし、使用するメモリははるかに少なく、平均して少ないステップです）。



ステップ数を見てみましょう。ブルートフォースで各対数を計算するには、平均で5193ステップが必要でした。5193は10331/2に非常に近い（曲線の次数の半分）。ベビーステップのジャイアントステップとロ・ポラードは、それぞれ152ステップと138ステップを使用しました。これらの2つの数値は、10331（101.64）の平方根に非常に近い値です。

さらなる考慮事項

これらのアルゴリズムの説明では、多くの数字を使用しました。それらを読むときは、注意することが重要です。多くの面でアルゴリズムを大幅に最適化できます。機器が改善される場合があります。特殊な機器を作成できます。



アプローチが今日実用的でないと思われる場合、これは改善できないという意味ではありません。これは、他のより良いアプローチがないことも意味しません（離散対数問題の複雑さの証拠がないことを忘れないでください）。

ショアアルゴリズム

最新の技術が適用できない場合、近い将来の技術についてはどうでしょうか？状況はますます懸念を引き起こしています：多項式時間で離散対数を計算できる量子アルゴリズムがすでにあります：時間の複雑さを持つショアアルゴリズム$$$O((\log n)^3)$ と空間の複雑さ $$$O(\log n)$ 。



量子アルゴリズムの効率は、状態の重ね合わせにあります。古典的なコンピューターでは、メモリセル（ビット）の値は1または0です。それらの間に中間状態はありません。一方、量子コンピューター（キュービット）のメモリセルは、不確実性の原理に従います。測定されるまで、完全に定義された状態はありません。状態の重ね合わせは、各量子ビットが値0と1を同時に持つことができることを意味しません（インターネットでよく書かれているように）。つまり、キュービットを測定するとき、0を観測する確率と1を観測する確率があります。量子アルゴリズムの仕事は、各キュービットの確率を変更することです。



この奇妙なことは、限られた数のキュービットで、多くの可能な入力データを同時に処理できることを意味します。たとえば、量子コンピューターに数字があることを伝えることができます$$$x$ 0と $$$n-1$ 。 必要なものすべて $$$\log n$ 代わりにキュービット $$$n \log n$ ビット。 次に、量子コンピューターにスカラー乗算を実行するように命令することができます $$$xP$ 。 結果として、すべての点によって与えられる状態の重ね合わせを $$$0P$ 前に $$$(n - 1)P$ つまり、ここですべてのキュービットを測定すると、次のいずれかのポイントが取得されます。 $$$0P$ 前に $$$(n - 1)P$ 確率で $$$1 / n$ 。



状態の重ね合わせの完全な力を理解できるように、これについて話しました。Shoreのアルゴリズムはそのようには機能しません。実際、より複雑です。「ふりをする」ことはできますが、$$$n$ 同時に、いくつかの段階で、この状態の数をいくつかに減らす必要があります。出力では、数ではなく1つの数が必要なためです（つまり、1つの対数を知っている必要があり、おそらく多くの誤った対数は必要ありません）。

ECCおよびRSA

さて、量子コンピューティングについては忘れましょう。これはまだ深刻な問題にはなりません。私は次の質問に答えたいと思います：RSAが既にうまく機能 するのに、なぜ楕円曲線に悩まされるのですか？



NISTは、同じレベルの保護を得るために必要なRSAとECCキーのサイズを比較した表を提示することで、簡単な答えを出しました。

RSAキーサイズ（ビット）	ECCキーサイズ（ビット）
1024	160
2048	224
3072	256
7680	384
15360	521

RSAキーサイズとECCキーサイズの間に線形関係はないことに注意してください（つまり、RSAキーサイズを2倍にした場合、ECCキーサイズを2倍にする必要はありません）。この表は、ECCが使用するメモリが少ないだけでなく、それにサインインしたキーの生成がはるかに高速であることを示しています。



しかし、これはなぜですか？答えは、楕円曲線上の離散アルゴリズムを計算するための最速のアルゴリズムは、ポラードρアルゴリズムとベイビーステップジャイアントステップであり、RSAの場合はより高速なアルゴリズムであるということです。特に、それらの1つは、数値フィールドをふるう一般的な方法です。：離散対数の計算に使用できる整数の因数分解アルゴリズム。数値フィールドをふるいにかける一般的な方法は、整数を因数分解するためのはるかに高速なアルゴリズムです。



これはすべて、DSA、Diffie-Hellman、El-Gamalなど、モジュラー演算に基づいた他の暗号システムに適用されます。

NSAの隠れた脅威

それでは、難しい部分に移りましょう。ここまで、アルゴリズムと数学について説明してきました。人々と話し合う時が来たので、事態はさらに複雑になっています。



覚えているなら、第3部で楕円曲線のいくつかのクラスが弱いと言ったので、疑わしいソースから信頼できる曲線を取得する問題を解決するために、定義ドメインのパラメーターにランダムシード値を追加します。また、標準のNIST曲線を見ると、検証可能なランダムであることがわかります。



「袖に何もない」という原則についてウィキペディアのページを読むと、次のことがわかります。

• MD5の乱数は、整数のサインから取得されます。
• Blowfishの乱数は、最初の数字から取得されます。 $$$\pi$ 。
• RC5の乱数は次から取得されます $$$e$ そして黄金比。

これらの番号は均等に分布しているため、ランダムです。そして、彼らには正当化があるので、彼らは疑いを引き起こしません。



ここで、次の疑問が生じます。NIST曲線のランダム生成値はどこから来るのでしょうか？回答：残念ながら、私たちは知りません。これらの値には理由がありません。



NISTが「かなり大きな」クラスの弱い楕円曲線を発見し、値を生成するさまざまな可能性のあるバリエーションを試し、脆弱な曲線を見つけた可能性はありますか？私はこの質問に答えることはできませんが、それは論理的で重要な質問です。 NISTが脆弱な乱数ジェネレーターを少なくとも正常に標準化したことがわかっています。（ジェネレーターは、奇妙なことに、楕円曲線に基づいています）。おそらく彼は多くの弱い楕円曲線も正常に標準化したのでしょうか？確認方法は？ まさか。



「検証可能なランダム」と「保護された」は同義語ではないことを理解することが重要です。対数タスクの複雑さやキーの長さは関係ありません。アルゴリズムがハッキングされた場合、私たちにできることは何もありません。



これに関して、悪用される可能性のある特別なドメインパラメータを必要としないため、RSAが勝ちます。 RSA（他のモジュラー算術システムと同様）は、当局を信頼できず、定義ドメイン用に独自のパラメーターを作成できない場合に適した代替手段となります。好奇心が強い場合：はい、TLSはNIST曲線を使用できます。 Googleにチェックインすると、接続時にECDHEとECDSAがprime256v1



（に基づいているsecp256p1



）に基づく証明書とともに使用されることがわかります。

以上です！

この記事をお楽しみください。楕円曲線上の暗号の現在の状態を理解するために必要な基本情報、用語、仮定を紹介しようとしました。私が成功すれば、既存のECCベースの暗号システムに対処し、より深いドキュメントを読むことで知識を広げることができます。この記事を書くとき、私は多くの詳細をスキップし、簡略化された用語を使用しましたが、そうでなければ、インターネット上に提示された情報を理解していないだろうと感じました。私は、情報の単純さと完全性の間の良い妥協点を見つけることができたと信じています。



ただし、この記事だけを読んだ後は、ECCに基づいた安全な暗号化システムを実装できないことに注意してください。セキュリティには、多くの微妙ではあるが重要な詳細に関する知識が必要です。スマート攻撃とSonyエラーの要件を覚えておいてください。これらは、安全でないアルゴリズムを作成する方法と、それらを簡単に悪用できる方法の2つの例です。



それでは、ECCの世界をさらに深く掘り下げてみたいとお考えなら、どこから始めますか？



まず、単純なフィールド上のワイエルシュトラス曲線を見ましたが、他のタイプの曲線とフィールドがあることを知っておく必要があります。

• Koblitzはバイナリフィールド上で曲線を描きます。これらは楕円形の曲線です$$$y^2 + xy = x^3 + ax^2 + 1$ （どこ $$$a$ -0または1）を含む有限体上 $$$2^m$ 要素（ここで $$$m$ — ). .
  
  
  
  nistk163
  
  
  
  , nistk283



nistk571
  
  
  
  ( , 163, 283 571 ).
• . $$$x^2 + xy = x^3 + x^2 + b$ （どこ $$$b$ — , ). , . nistb163
  
  
  
  , nistb283



nistb571
  
  
  
  .
  
  
  
  , , , .
• $$$x^2 + y^2 = 1 + d x^2 y^2$ （どこ $$$d$ — 0 1). , , , , ( $$$P \ne Q$ 、 $$$P = Q$ 、 $$$P = -Q$ , ...). (side-channel attack), , , .
  
  
  
  ( 2007 ), , Certicom NIST, .
• Curve25519とEd25519は、それぞれECDHとECDSAバリアント用に作成された2つの特別な楕円曲線です。エドワーズ曲線と同様に、これらの2つの曲線は高速であり、サードパーティのチャネルに対する攻撃を防ぐのに役立ちます。エドワーズ曲線と同様に、これらの2つの曲線はまだ標準化されておらず、一般的なソフトウェアでは使用されていません（2014年以降Ed25519キーペアをサポートしていたOpenSSHを除く）。

ECCの実装の詳細に興味がある場合は、OpenSSLおよびGnuTLSのソースを読むことをお勧めします。



そして最後に、アルゴリズムの安全性と効率ではなく、数学的な詳細に興味がある場合は、次のことを知る必要があります。

• 楕円曲線は、属1の代数多様体です。
• 射影幾何学では無限遠点が研究されます。それらは、均一な座標を使用して表すことができます（ただし、楕円曲線の暗号化には射影幾何のほとんどのプロパティは必要ありません）。

そして、場の理論とともに有限の場を研究することを忘れないでください。このトピックに興味がある場合は、そのようなキーワードを探す価値があります。この記事は正式に終了します。フレンドリーなコメント、ツイート、手紙をありがとう。多くの人が、関連するトピックに関する他の記事を書くかどうか尋ねました。私の答えは：多分。あなたはあなたの提案を送ることができますが、私は何も約束しません。