Kソート：n <= 7,000,000のピラミッド型アルゴリズムよりも優れた新しいアルゴリズム

翻訳者から。 クイックソート変更の統計分析に関するarxiv.orgの2011年の記事の翻訳。 確かに、説明されたオプションを直感的に使用する人がいます。 以下は、n <= 7,000,000の有効性の数学的な正当化です。

はじめに

キーワード

内部ソート; 均一な分布; 平均時間の複雑さ 統計分析; 統計的評価



Sundarajan and Chakraborty [10]は、交換を削除するクイックソートの新しいバージョンを導入しました。 Kreisat [1]は、アルゴリズムが他のバージョンのクイックソートと十分に競合することに注目しました。 ただし、補助配列を使用するため、空間の複雑さが増します。 ここでは、ヘルパー配列を削除した2番目のバージョンを提供します。 Kソートと呼ばれるこのバージョンは、一様分布U [0、1] （統計的にはおよその翻訳）の入力データに対して、有意な配列サイズ（n <= 7,000,000）でピラミッド要素よりも速く要素を配置します。



1.はじめに



内部ソート方法がいくつかあります（すべてのアイテムをメインメモリに保存できます）。 バブルソートなどの最も単純なアルゴリズムは、通常、n個のオブジェクトを順序付けるO（n ² ）の時間を必要とし、小さなセットに対してのみ有用です。 最も一般的な大規模なセットアルゴリズムの1つはクイックソートで、平均でO（n * log ₂ n）を、最悪の場合はO（n ² ）を取ります。 Knut [2]のソートアルゴリズムの詳細をご覧ください。



Sundarajan and Chakraborty [10]は、交換を削除するクイックソートの新しいバージョンを導入しました。 Khreisat [1]は、このアルゴリズムが、SedgewickFast、Bsort、およびn [3000. 200 000]のシングルトンソートなど、クイックソートの他のバージョンと競合することを発見しました。 比較アルゴリズムは交換よりも優先されるため、交換を削除しても、このアルゴリズムの複雑さは従来のクイックソートの複雑さと変わりません。 言い換えると、このアルゴリズムには、クイックソート、つまりO（n * log ₂ n）およびO（n ² ）に匹敵する平均および最悪の複雑さがあり、これもKreisat [1]によって確認されています。 ただし、補助配列を使用するため、空間の複雑さが増します。 ここでは、補助配列が削除されたKソートと呼ばれる、ソートの2番目の改良バージョンを提供します。 K-sortを使用した要素のソートは、ピラミッド型よりも高速で、均一に分散された入力U [0、1]の有意な配列サイズ（n <= 7,000,000）であることがわかりました。



1.1 Kソート

Step-1: Initialize the first element of the array as the key element and i as left, j as (right+1), k = p where p is (left+1). Step-2: Repeat step-3 till the condition (ji) >= 2 is satisfied. Step-3: Compare a[p] and key element. If key <= a[p] then Step-3.1: if ( p is not equal to j and j is not equal to (right + 1) ) then set a[j] = a[p] else if ( j equals (right + 1)) then set temp = a[p] and flag = 1 decrease j by 1 and assign p = j else (if the comparison of step-3 is not satisfied ie if key > a[p] ) Step-3.2: assign a[i] = a[p] , increase i and k by 1 and set p = k Step-4: set a[i] = key if (flag = = 1) then assign a[i+1] = temp Step-5: if ( left < i - 1 ) then Split the array into sub array from start to i-th element and repeat steps 1-4 with the sub array Step-6: if ( left > i + 1 ) then Split the array into sub array from i-th element to end element and repeat steps 1-4 with the sub array
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

デモンストレーション

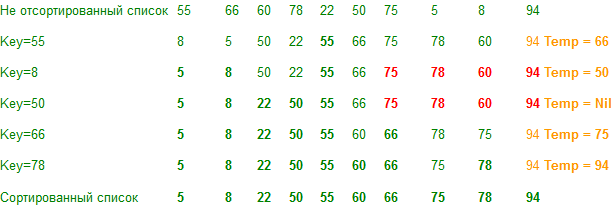
ご注意 補助配列に1つの値がある場合、処理する必要はありません。



2.経験的（中程度の時間の複雑さ）



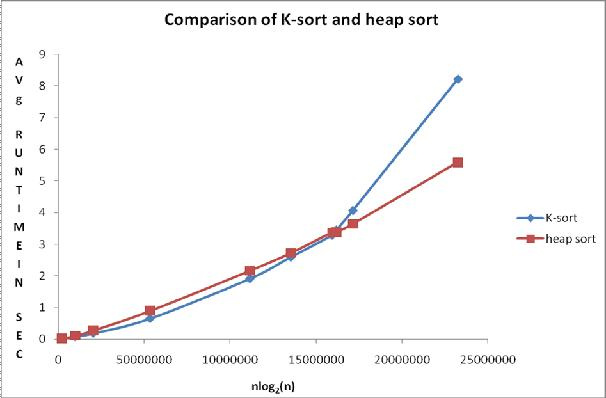
コンピューター実験は、さまざまな入力に対して実行される一連のコードです（Sachs [9]を参照） 。BorlandInternational Turbo 'C ++' 5.02でコンピューター実験を行うことにより、平均ソート時間を秒単位で比較できました（平均値は500を超えました） Kソートとヒープのnの異なる値に対して。 モンテカルロシミュレーション（ケネディとジェントル[7]を参照）を使用して、サイズnの配列を独立した連続した同種U [0、1]バリエーションで満たし、別の配列にコピーしました。 これらの配列は、比較アルゴリズムによってソートされました。 表1と図 1は経験的な結果を示しています。











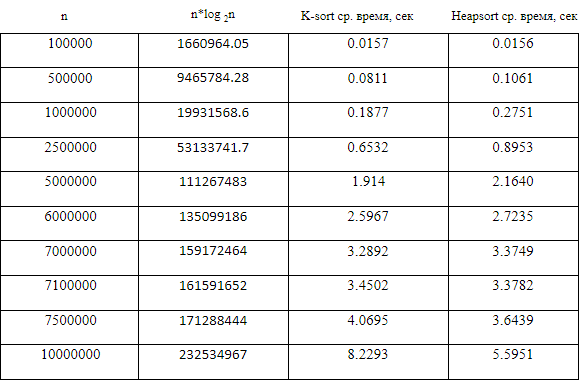
図 1比較チャート



検討中のソートの連続的な均一分布U（0,1）から観測された平均時間値を表1に示します。図1と表1は、アルゴリズムの比較を示しています。



表1から作成されたグラフのポイントは、配列サイズが7,000,000エレメント以下の場合、Kソートの平均ランタイムがヒープソートの平均ランタイムよりも短く、この範囲を超えると、ヒープソートが高速に実行されることを示しています。



3. Minitabバージョン15を使用した経験的結果の統計分析



3.1。 Kソートの分析：n * log 2（n）およびnによる平均ソート時間y（K）の回帰









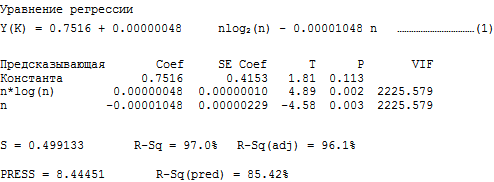
Rは、大きな標準化された残基を使用した観測を表します。

図 2.1-2.4は、追加のモデルテストの視覚的な概要を示しています。















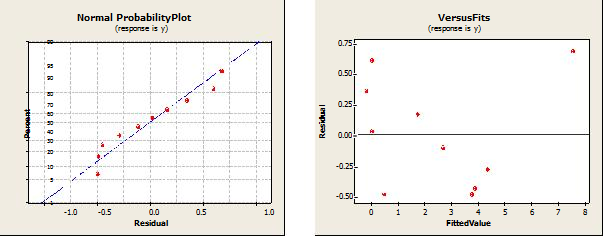
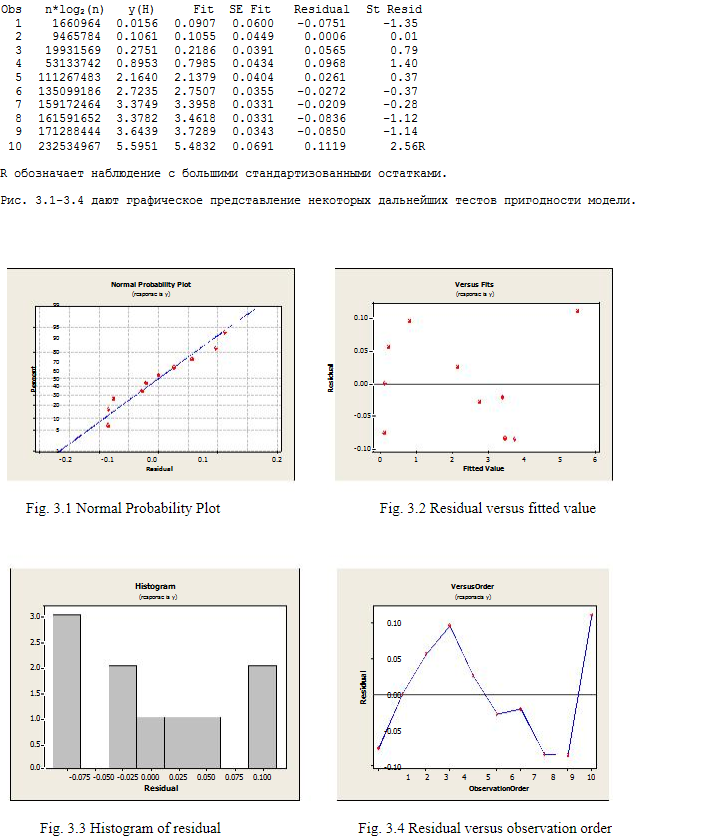
4.ディスカッション部



Kソートとヒープソートの両方で、回帰モデルでn * log（n）によって導入された二乗の合計が、nによって取得された合計と比較して重要であることがわかります。 両方のアルゴリズムの平均複雑度はO（n * log ₂ n）であることを思い出してください。 したがって、実験結果は理論を裏付けています。 クイックソートおよびヒープソートでO（nlog ₂ n）の複雑さにつながる数学演算子を見るとn項が含まれるため、モデルにn項を保存しました（Knuth [2]を参照）。



平均ケースの比較回帰式は、y（K）からy（H）を引くだけで得られます。



y（K）-y（H）= 0.52586 + 0.00000035 n * log2（n）-0.00000792 n ....... ..（3）



方程式（1）、（2）、（3）の利点は、両方のソートアルゴリズムの平均実行時間と、実行するのが面倒なnの値が大きい場合でもその差を予測できることです。 このような「安価な予測」はコンピューター実験のモットーであり、ランダムでないデータに対しても確率的モデリングを行うことができます。 別の利点は、予測を行うために入力のサイズのみを知るだけで十分であることです。 つまり、（答えが固定されている）入力全体は必要ありません。 したがって、確率モデルによる予測は、安価であるだけでなく、より効率的です（Saks、[9]）。



プログラムの実行時間を直接操作する場合、実際には有限範囲の統計的推定値を計算することに注意することが重要です（コンピューター実験は無限のサイズを入力するために実行することはできません）。計算操作を正確に計算するのではなく重量を量るので、さまざまな操作を概念的な評価に混ぜることができますが、数学的な複雑さは操作に固有のものです ui。 ここでは、動作時間をその重量とみなします。 正式な定義やその他の特性を含む統計的推定の一般的な議論については、Chakraborty and Soubik [5]を参照してください。 Chakraborty、Modi、およびPanigrahi [4]も参照して、統計的推定が並列計算の理想的なフロンティアである理由を理解してください。 統計的評価の仮定は、重みに有限範囲の数値が割り当てられたコンピューター実験を実行することにより得られます。 これは、関連する評価の信頼性が、コンピューター実験の適切な設計と分析に依存することを意味します。 VLSI設計、燃焼、熱伝達など、他のアプリケーションを使用したコンピューター実験に関する関連文献は（Fang、Lee、およびSugianto、[3]）にあります。 レビューも参照してください（Chakraborty [6]）。



5.今後の作業の結論と提案



Kソートは、最大7,000,000個のソート要素の数がヒープよりも明らかに高速ですが、平均的なケースでは両方のアルゴリズムのO（n * log ₂ n）複雑度順序は同じです。 今後の作業には、この改善されたバージョンのパラメーター化された複雑さに関する研究（Mahmoud、[8]）が含まれます。 最後のコメントとして、少なくともn <= 7,000,000のKソートを強くお勧めします。



ただし、最悪の場合でもヒープソートを選択することに同意します。これは、最悪の場合でもO（n * log ₂ n）の複雑さをサポートしているためです。



NB継続作業、2012年