キューシステムを作成する前に知っておく必要があること

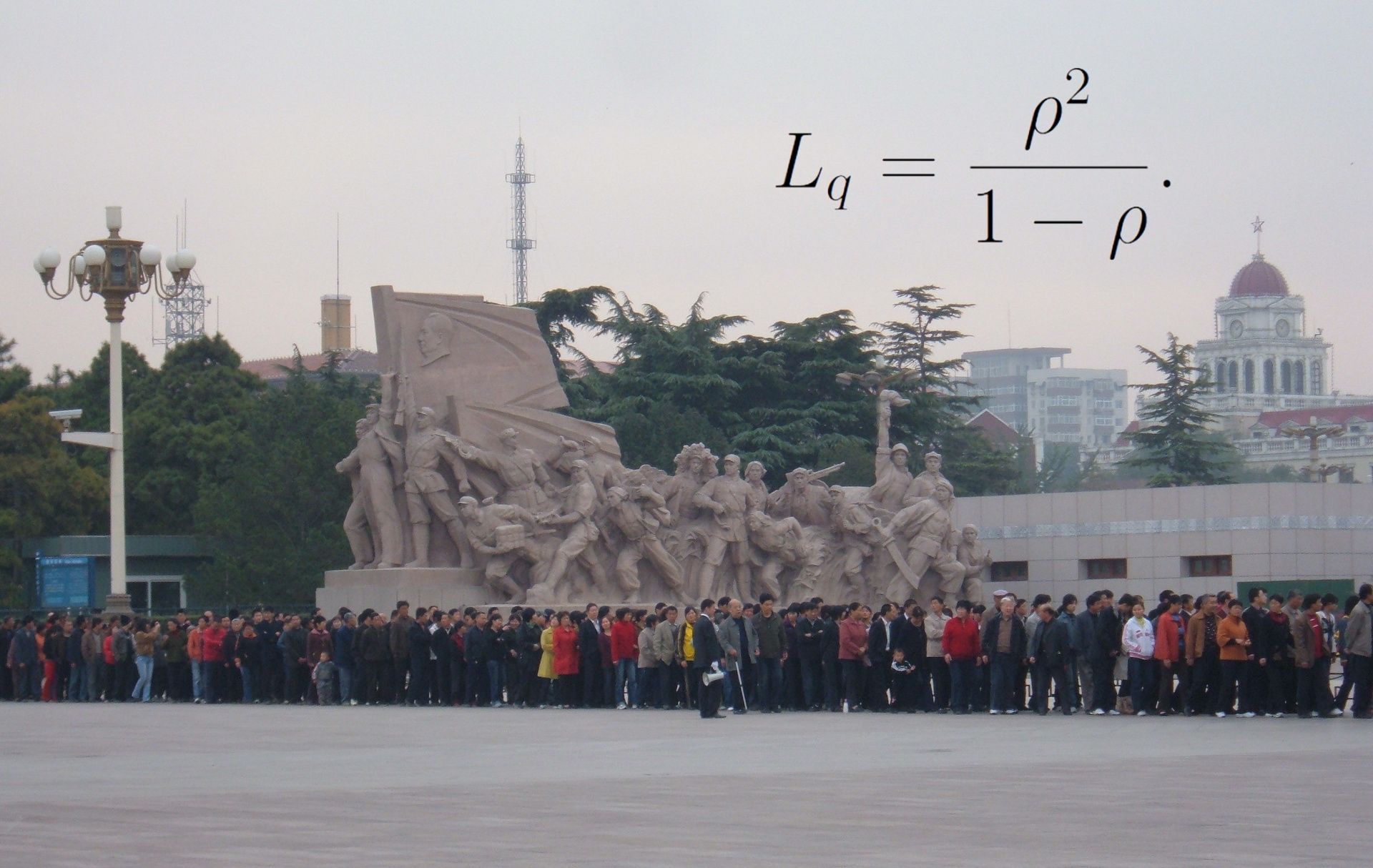
私が取り組んでいるプロジェクトでは、分散データ処理システムを使用しています。まず、数十台のマシンが同時にいくつかのメッセージを生成し、次にこれらのメッセージがキューに送信され、3つのスレッドがキューから抽出され、最終処理後にRedisデータベースにアップロードされます。 同時に、要件があります。メッセージを生成するマシンでのイベントの「生成」から、処理されたデータのデータベースへのポストまで、90％のケースで4秒を超えてはなりません。



ある時点で、努力が費やされたにもかかわらず、この要件を満たしていないことが明らかになりました。 いくつかの測定を行い、キューの理論を少し検討した結果、プロジェクトが始まったばかりの数か月前に自分に伝えたい結論に至りました。 過去に手紙を送ることはできませんが、メモを書くことはできます。おそらく、自分のシステムにキューを適用することを考えている人の悩みを取り除くでしょう。



メッセージが処理のさまざまな段階で費やす時間を測定することから始め、次のようなものを得ました（秒単位）：







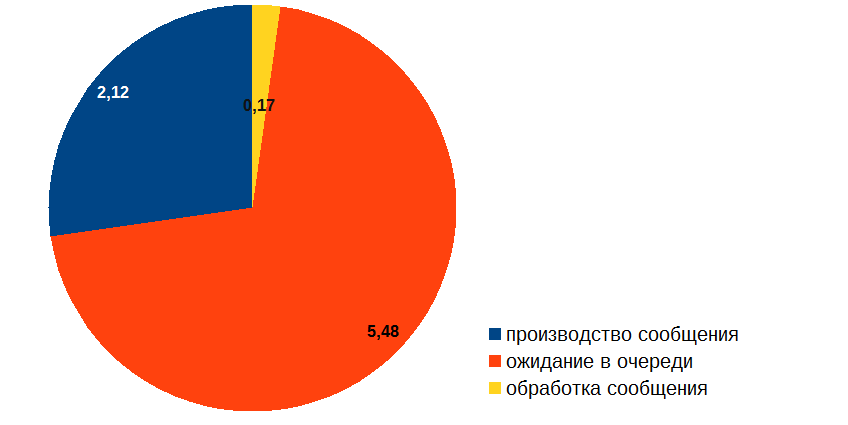
したがって、メッセージの処理にはかなり時間がかかるという事実にもかかわらず、メッセージのほとんどはキュー内でアイドル状態です。 これはどのようにできますか？ そして、最も重要なこと：それをどう扱うか？ 実際、上の図が通常のコードのプロファイリングの結果である場合、すべてが明白になります。「赤」の手順を最適化する必要があります。 しかし、問題は、私たちの場合、「レッド」ゾーンでは何も起こらず、メッセージが並んでいるだけだということです！ メッセージの処理（ダイアグラムの「黄色」の部分）を最適化する必要があることは明らかですが、疑問が生じます。この最適化はキューの長さにどのように影響し、望ましい結果を得ることができる保証はどこにありますか？



キュー （ オペレーションズリサーチのサブセクション）の理論は、キュー内の待機時間の確率的推定を扱っていることを思い出しました。 当時、大学ではこれを経験していなかったため、しばらくの間、ウィキペディア、PlanetMath、オンラインレクチャーに没頭しなければなりませんでした。などなど



キューイング理論の分析結果はかなり深刻な数学にあふれており、これらの結果のほとんどは20世紀に得られました。 これらすべてを研究することは魅力的な活動ですが、非常に長く骨の折れる活動です。 私は少なくともなんとかしてそれに飛び込むことができたとは言えません。



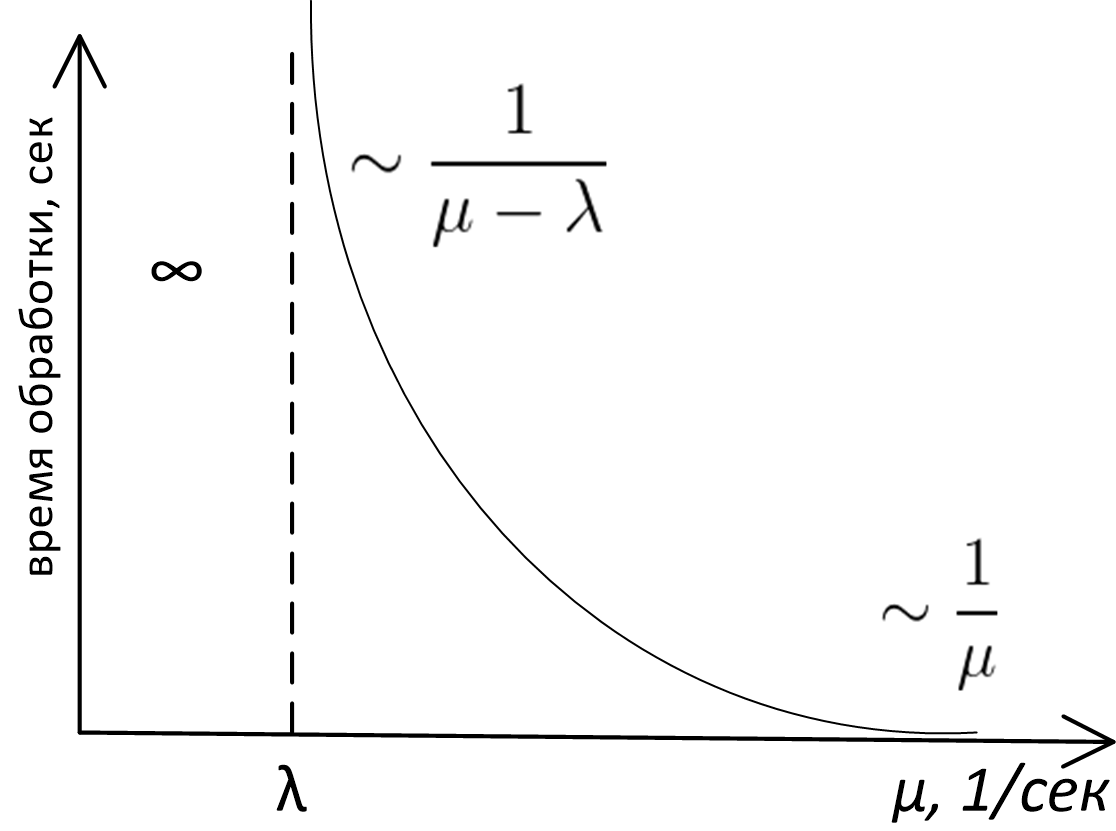
それでも、キューイング理論の「トップ」のみを調べたところ、私たちのケースで実際に適用できる主な結論は表面にあり、正当化には常識が必要であり、依存グラフに表示できることがわかりましたサーバー帯域幅のキューを使用したシステムでの処理時間、ここでは次のとおりです。







ここに

• $$$\ mu$ -サーバー帯域幅（1秒あたりのメッセージ数）
• $$$\ラムダ$ -リクエストの平均頻度（1秒あたりのメッセージ数）
• 縦軸は、平均メッセージ処理時間を表します。

このグラフの正確な分析形式は、キューイング理論の研究の主題であり、キューM / M / 1、M / D / 1、M / D / cなどの場合（それが何であるかわからない場合- ケンドールの表記法を参照）この曲線は、まったく異なる式で記述されます。 それでも、キューがどのモデルで記述されていても、この関数の外観と漸近的な動作は同じです。 これは、単純な推論で証明できますが、これを行います。



まず、グラフの左側を見てください。 次の場合、システムが安定しないことは明らかです。 $$$\ mu$ （帯域幅）少ない $$$\ラムダ$ （受信の頻度）：処理するメッセージの頻度は、処理できる頻度よりも大きくなり、キューは無期限に大きくなり、深刻な問題が発生します。 一般的に、ケース $$$\ mu <\ lambda$ -常に緊急。



右側のグラフが漸近的に傾向があるという事実 $$$1 / \ mu$ 、また非常に単純であり、その証明のために深い分析を必要としません。 サーバーが非常に高速に動作する場合、実際にはキューで待機することはなく、システムで費やす合計時間はサーバーがメッセージの処理に費やす時間に等しくなります。 $$$1 / \ mu$ 。



すぐに明らかではないかもしれませんが、 $$$\ mu$ に $$$\ラムダ$ 右側では、キューでの待機時間が無限に長くなります。 実際：場合 $$$\ mu = \ lambda$ 、これは、平均メッセージ処理速度が平均メッセージ到着率に等しいことを意味し、直観的にはこの状況ではシステムが対処する必要があるようです。 ある時点で時間とサーバーのパフォーマンスのグラフがあるのはなぜですか $$$\ラムダ$ 無限に飛ぶが、何とかこのように動作しません：







しかし、この事実は、深刻な数学的分析に頼ることなく確立できます！ これを行うには、メッセージを処理するサーバーが2つの状態になる可能性があることを理解するだけで十分です：1）仕事で忙しい2）すべてのタスクを処理したためにアイドル状態であり、新しいタスクがまだキューに到着していない



キュー内のタスクは不均等になります。「密度が高く、頻度が低い」場合：単位時間あたりのイベント数は、いわゆるポアソン分布で表されるランダム変数です。 特定の時間間隔でタスクがほとんど発生せず、サーバーがアイドル状態だった場合、将来のメッセージの処理に使用するために、アイドル状態の時間を「保存」することはできません。



したがって、サーバーのダウンタイムが原因で、システムからのイベント終了の平均速度は常にサーバーのピークスループットよりも低くなります。



同様に、平均出口速度が平均入口速度よりも遅い場合、これはキュー内の平均待機時間の無限の延長につながります。 入力イベントのポアソン分布と一定または指数処理時間のキューの場合、飽和点付近の期待値は比例します

$$

$$\ frac {1} {\ mu- \ lambda}。$$

結論

したがって、スケジュールを見て、次の結論に達します。

• キューのあるシステムでのメッセージ処理時間は、サーバーの帯域幅の関数です $$$\ mu$ および平均メッセージ率 $$$\ラムダ$ 、さらに簡単：それはこれらの量の比率の関数です $$$\ rho = \ lambda / \ mu$ 。
• キューを使用してシステムを設計する場合、メッセージの平均到着頻度を推定する必要があります $$$\ラムダ$ サーバーの帯域幅を配置します $$$\ mu >> \ラムダ$ 。
• 比率に応じて、キューを持つすべてのシステム $$$\ラムダ$ そして $$$\ mu$ 次の3つのモードのいずれかになります。
  
  
  
  
  1. 緊急モード- $$$\ mu \ leq \ lambda$ 。 システムのキューと処理時間は無制限に増加します。
  2. 飽和モードに近い： $$$\ mu> \ラムダ$しかし、それほどではありません。 この状況では、サーバー帯域幅のわずかな変更が、システムパフォーマンスパラメーターに大きく影響します。 サーバーを最適化する必要があります！ さらに、わずかな最適化でさえ、システム全体にとって非常に有益です。 サービスのメッセージ到着率とスループットの推定値は、システムが「飽和点」のすぐ近くで機能することを示していました。
  3. 「ほとんど並んでいない」モード： $$$\ mu >> \ラムダ$ 。 システムで費やされる合計時間は、サーバーが処理に費やす時間とほぼ同じです。 サーバーの最適化の必要性は、合計処理時間に対するサブシステムのキューへの寄与などの外部要因によって既に決定されています。

これらの質問に対処した後、イベントハンドラーの最適化に進みました。 結果は次のとおりです。









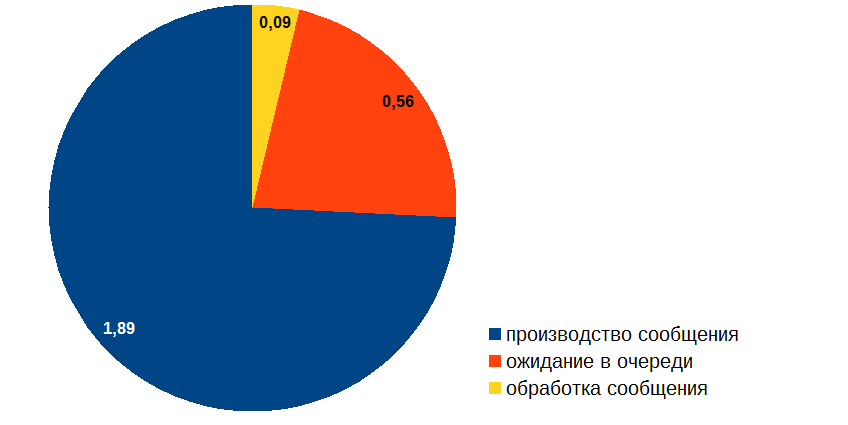
OK、メッセージの作成時間を最適化できるようになりました！



また、「 キューを処理するための原則とテクニック」を読むことをお勧めします 。