🤾🏾 🎥 🏦 タスク：より小さな境界線を持つ三角形を見つける 👆🏾 🥕 🏇🏽

私は偶然この仕事に出会いました。私の友人は、政権を卒業してから1年後、再び勉強することを決め、入学の準備を始めました。そのため、何かを繰り返して覚えておく必要があり、新しいもので整理する必要があります。ここで、彼女はいくつかのタスクに座って、私は通り過ぎました。タスクは（学校レベルで）非常に簡単に見えましたが、少し考える必要があります。

そのため、ここで検討するタスクは次のように聞こえます。角度とその中の点を考えると。このポイントを通して、結果の三角形の周囲が最小になるように、コーナーの両側に端を持つセグメントを描画します。

問題は、ファニャーノ問題の証明の一部です。

Fagnano自体のタスクは次のとおりです。

すべての種類の三角形が考慮されます。

D E F

$DEF$ トップス

D

$D$ 、

E

$E$ そして

F

$F$ 側にある

B C

$BC$ 、

A C

$AC$ そして

A B

$AB$ 鋭い三角形

A B C

$ABC$ それに応じて。すべての三角形DEFのことを証明します。三角形のオルソセントリック三角形は最小の境界を持っています

A B C

$ABC$ 。

直交三角形

直交三角形（直交三角形）は、頂点が元の三角形の高さのベースとして機能する三角形です。

頭に浮かぶ最初の考えは、おそらく垂直を構築することです（側面への最短距離として）。表示ポイント

D

$D$ 対称的に

A C

$AC$ そして

A B

$AB$ （ポイントを獲得します

D_{1}

$D_1$ そして

D_{2}

$D_2$ ）

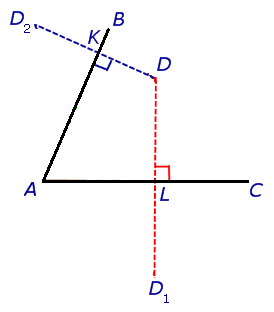
垂線と角度の側面の交点を接続するようにすぐに誘惑されるかもしれません

B a c

$Bac$ 。その後、「やった」という誤った印象があり、

K D L

$KDL$ -これは同じ三角形です。

そうではありません。三角形の2辺が最短（直線に垂直）であるという事実は、三角形の周囲をまだ最小にしない。

実際、最小の境界を持つ三角形の検索では、次のステートメントを使用します。2点間の最短距離は直線です。追加の構造は、目的の三角形のすべての辺の長さが直線上にあるという事実につながるはずです。ドットをつなぐ

D_{1}

$D_1$ そして

D_{2}

$D_2$ 。ライン交点

D_{1} D_{2}

$D_1D_2$ 角度の辺は、三角形の残りの望ましい頂点です。

F k

$Fk$ そして

E L

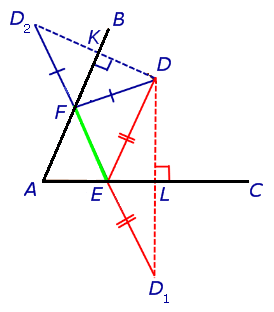
$EL$ 中央値と高さ（ドット

D

$D$ 三角形の辺に対して対称的に表示されます）

D_{2} D F

$D_2DF$ そして

D D_{1} E

$DD_1E$ それぞれ、三角形を意味します

D_{2} D F

$D_2DF$ そして

D D_{1} E

$DD_1E$ -二等辺。三角形の周囲が

D E F

$DEF$ セグメントの長さと等しい

D_{1} D_{2}

$D_1D_2$ 。より小さな境界を持つ三角形が見つかりました。

他のポイントを取りましょう（

F

$F$ そして

E

$E$ ）角の両側に。

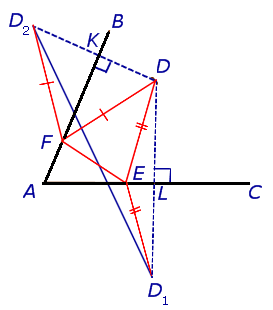
この三角形の周囲

D E F

$DEF$ セグメントの長さよりも大きいことが判明

D_{1} D_{2}

$D_1D_2$ 。

以上です。皆さんに幸運を！

タスク：より小さな境界線を持つ三角形を見つける

More articles: