みなさんこんにちは。私たちはgithubとsticksからコンピュータービジョンの自動車ビジョンを収集し続けています（ここから始めます）。今日、スマートフォンのモーションセンサー（加速度計、ジャイロスコープ、GPS受信機）をAndroidに接続し、簡単なセンサーフュージョンを習得し、最後にトレーニングサンプルを収集するためのコードで閉じます。ボーナス- 外国の競争の輸入代替の一部として、ビデオおよび1時間以上のタグ付きデータと同期したすべてのセンサーを記録するためのAndroidアプリケーション。すべてのコードはまだgithubにあります。

これらは3軸MEMS加速度計とジャイロスコープであり、非常に有用です。

簡単に言えば、詳細については、前の投稿へようこそ。最終目標は、フロントガラスからのビデオのフレームから車の制御アクションを生成できるシステムを訓練することです（ステアリング角度と希望の速度または加速度）。車が人によって制御されるレースのビデオ、および回転角と速度に関する時間同期情報最新の車では、このデータはCANバス経由で読み取ることができますが、最初に特別なCANアダプターを購入して接続する必要があります第二に、メーカーごとに異なるプロトコルとデータ形式の復号化に対処するために、この大騒ぎの代わりに、他のものに接続されていない通常のスマートフォンの生データから間接的に制御アクションを計算します。

最後のシリーズでは、ビデオSLAM ライブラリーを使用して、ビデオフレームのみに基づいて水平面内を回転する車の角速度を決定する方法を学びました。残念ながら、実際には、このライブラリはデバイスの並進速度を非常に不正確に計算します。並進速度がわからなければ、角速度はオートパイロットのステアリングコンポーネントを個別に訓練することもできません。 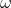$\オメガ$ ステアリングホイールの回転角度の組み合わせに依存します（同様に、回転半径）および車の並進速度。

並進速度を得るために、今日、ビデオ処理からモーションセンサーに切り替えています。モーションセンサーは、ほぼすべてのスマートフォン（GPS受信機、加速度計、ジャイロスコープ）に搭載されています。それぞれの長所と短所を見て、情報を組み合わせて、ビデオの各フレームの瞬時の速度を取得しましょう。さらに、ジャイロスコープから回転に関する情報も取得します。これにより、より気まぐれな光学SLAMと、必要なスマートフォンのカメラのキャリブレーションを放棄できます。その結果、新しいデータ収集プロセスは3回の「ボタンの押下」に縮小されました。アプリケーションを電話にかける-到着時にトラックを記録する-コンピューターで1つのコマンドで処理する。

結果として、並進速度と回転速度を持つフレームごとの注釈を取得します。

利用可能なモーションセンサー

アンドロイドで動作します。プラットフォームに関係なく-英語を知っている人のために、さまざまなセンサーからの情報がどのように校正を改善し、エラーを減らすことができるかについての興味深いビデオをご覧ください。モーションセンサー（加速度計とジャイロスコープ）と位置（GPS）に興味があります。

APIの観点から見ると、すべてが単純です。ユーザーに許可を求め、更新をサブスクライブし、センサーと測定時間でイベントのストリームを取得します。詳細はソースにあります。

センサーの長所と短所を考慮してください。

GPS

結局のところ、GPSは、少なくとも比較的広い空間で、並進速度を決定することに90％成功しています。 GPSからの形式はLocationです。

絶対位置（緯度、経度）の評価。
座標精度評価-推定値の68％の信頼円半径。つまり、測定値の約68％で、デバイスの現在の位置は推定値を中心とした所定の半径内にある必要があります。原則として、多かれ少なかれオープンスペースでは、3〜4 m以内の精度が得られます。
過去の測定されたGPS位置から推定された絶対速度（方向なし）。

GPSデータの大きな利点は、 測定誤差が独立していることです。つまり、時間の経過とともに累積することはありません。新しい測定値は、以前の測定数と誤差の数の影響を受けません。これは、アプローチの残りの部分を担う非常に重要なプロパティです。

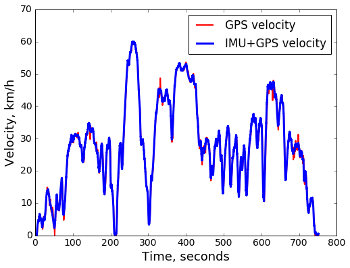
欠点は、 測定が 1秒間に約1回行われることはめったにないことであり、 測定をもっと頻繁に行うだけでは意味がありません。デバイスを動かすことは測定誤差に匹敵します。その結果、まずGPSデータは速度の変化に遅れて反応し、次にノイズを除去するのがより困難になります。このため、時間内に隣接する測定値を確認する必要があり、データのあいまいさをさらに悪化させます。 GPS速度チャートの例を次に示します。

最初の25秒（一定の加速とGPS測定の推定遅延）および30〜40秒のノイズはここでは疑わしいです。シードについては、加速度計とジャイロスコープからのデータを処理した後の同じグラフ：

ご覧のとおり、両方のインジケータに改善があります。加速に早く対応し、爆発は35秒でスムーズになります。

慣性センサー：加速度計とジャイロスコープ

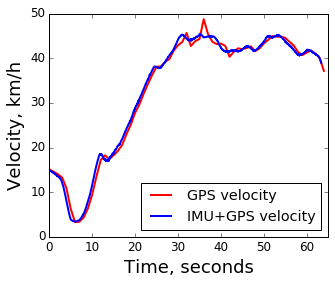
慣性センサーは、加速度、線形（加速度計）、および求心性（ジャイロスコープ）を測定します。それらの測定結果は、前の時点に対するデバイスの動きの変化の推定値です。数学的には、これはデバイスに接続された 座標系の使用で表現されます：

加速度計は、デバイスの3軸であるジャイロスコープに沿って直線加速度を与えます。これは、同じ3軸の周りの角速度です。

さらに慣性センサー-400 Hz以上で非常に頻繁に測定される可能性があります。これは、約30 Hzのビデオフレーム周波数のオーダーをカバーします。主な欠点は、固定座標系との通信の欠如です。センサーは前の位置に対する変化のみを測定することができるため、結果を固定座標系で計算するには、読み取り値を経時的に積分する必要があり、 測定誤差は累積します -測定期間が長くなるほど、次の瞬間の合計誤差が大きくなります

ご覧のとおり、GPSセンサーと慣性センサーには鏡の反対側の長所と短所があります。つまり、両方のソースの長所を組み合わせる必要があります。

センサーフュージョン：情報の結合

GPSおよび慣性センサーからデータを記録したら、以下を評価する必要があります。

高時間分解能の絶対並進速度。
車両の垂直軸周りの回転角速度（つまり、任意の時点での道路の平面内）。

前回の投稿ですでに水平回転を計算しましたが、判明したように、古い方法（ビデオ分析による）は、ジャイロスコープを直接操作するよりも複雑で気まぐれなので、アプローチを変更する方が良いでしょう。

並進速度

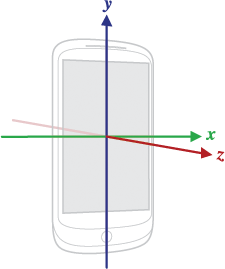
それははるかに簡単に思えます。定義から知っている学校物理学から

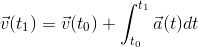
$\ vec {v}（t_1）= \ vec {v}（t_0）+ \ int_ {t_0} ^ {t_1} \ vec {a}（t）dt$

ただし、固定の座標系で速度が必要であり、加速度計の座標系はデバイスとともに回転します。デバイスの座標系から静止座標系への回転行列をR

表し、次に

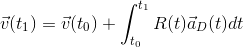
$\ vec {v}（t_1）= \ vec {v}（t_0）+ \ int_ {t_0} ^ {t_1} R（t）\ vec {a} _ {D}（t）dt$

どこで 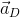$\ vec {a} _ {D}$ -デバイスの座標軸に沿った加速度。次に、ジャイロスコープによって測定された回転を単に積分することにより、回転行列を取得します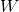（回転行列の導関数であり、3つの軸の周りの角速度を知ることで計算できます）。

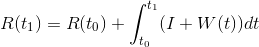
$R（t_1）= R（t_0）+ \ int_ {t_0} ^ {t_1}（I + W（t））d t$

それだけですか？そこには、真空中の球面加速度計でのみ機能します。テーブルの上に動かずに横たわっているスマートフォンからの実際のデータを見てみましょう。

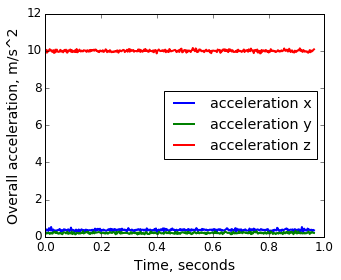
軸ごとの生の加速度計測定値

観察：

加速度計は重力の効果を電話の加速の効果から根本的に区別できないため、重力は自動的に差し引かれません。したがって、方向を手動で決定して調整する必要があります。理論的には、AndroidはOSレベルでこのような修正を提供しますが、実際には私にとってはうまくいきませんでした。
3つの軸に沿った合計加速度/吸引力は10 m / s ²を超えます。これはテーブルから非常に離れており、9.81 m / s 2-10分で0.2 * 600 = 120 m / s = 432 km / hになります。

2番目の実験-画面を上にしてテーブルに横たわっている電話機からの合計加速度を記録し、次に-画面を下にして、比較します。

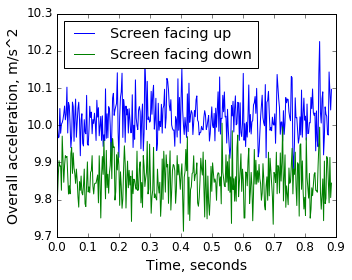
全体的に測定された加速画面の上下比較

観察：

0.15 m / s ^2を超える差^は、単に方向の変化によるものです。つまり、ローカル座標系に顕著な系統誤差があります。
0.05 m / s ²の領域で一定の測定ノイズが発生し、上記の積分からわかるように、エラーは時間の経過とともに蓄積します。そして、ノイズが合計されると、バイアスのないノイズでも（つまり、測定値の数学的期待値が真の値と一致する場合）、中心極限定理に従って、 n

測定値の合計の分散は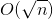 $O \左（\ sqrt {n} \右）$ 。

ノイズモデルと自動キャリブレーション

そのため、固定座標系で実際の加速度を得るには、「生の」加速度計測定値の修正が必要です。単純なモデルを適用します：

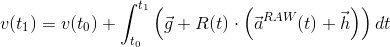
$v（t_1）= v（t_0）+ \ int_ {t_0} ^ {t_1} \ left（\ vec {g} + R（t）\ cdot \ left（\ vec {a} ^ {RAW}（t）+ \ vec {h} \右）\右）dt$

どこで

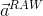$\ vec {a} ^ {RAW}$ -デバイスの座標系での加速度計の生の測定値。
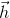$\ vec {h}$ -デバイスの座標系でも、加速度計の系統誤差の補償。
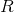-デバイスの座標系から固定座標系への回転行列。
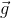$\ vec {g}$ -固定座標系での一定の重力。

ジャイロスコープから角速度を積分することで回転行列を取得しますが、残りのパラメーターは不明です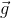（ $\ vec {g}$ なぜならスマートフォンの初期の向きは不明です）。キャリブレーションパラメーターを見つけると、GPSデータに役立ちます。 GPSの測定値はかなり正確であることを思い出してください。そのため、慣性センサーによって計算される速度は、GPSデータによる速度に近いはずです。この直感を最適化問題として形式化します。隣接するGPS測定の間隔（1秒程度）ごとに、慣性データに従って移動距離を計算し、GPSデータとターゲット関数に従って、記録時間全体にわたってL2メトリックを割り当てます。

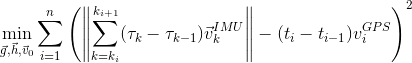
$\ min _ {\ vec {g}、\ vec {h}、\ vec {v} _0} \ sum_ {i = 1} ^ n \ left（\ left \ | \ sum_ {k = k_i} ^ {k_ {i +1}}（\ tau_k-\ tau_ {k-1}）\ vec {v} _k ^ {IMU} \ right \ |-（t_i-t_ {i-1}）v ^ {GPS} _i \ right） ^ 2$

どこで

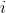-GPS測定インデックス。
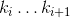$k_i \ドットk_ {i + 1}$ -GPS i

とi+1

測定間隔に含まれる慣性センサーの測定指標。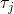
$\ tau_j$ 時間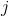慣性センサーの測定。

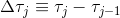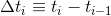また、 $\デルタ\ tau_j \ equiv \ tau_j-\ tau_ {j-1}$ そして $\デルタt_i \ equiv t_i-t_ {i-1}$ 、加速度計の生の測定値に補正を代入すると、目的関数の最終形式が得られます。

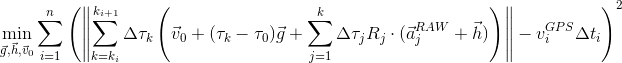
$\ min _ {\ vec {g}、\ vec {h}、\ vec {v} _0} \ sum_ {i = 1} ^ n \ left（\ left \ | \ sum_ {k = k_i} ^ {k_ {i +1}} \ Delta \ tau_k \ left（\ vec {v} _0 +（\ tau_k-\ tau_0）\ vec {g} + \ sum_ {j = 1} ^ k \ Delta \ tau_j R_j \ cdot（\ vec {a} _j ^ {RAW} + \ vec {h}）\ right）\ right \ |-v ^ {GPS} _i \ Delta t_i \ right）^ 2$

恐ろしく見えますが、実際は単純な2次関数であり、導関数を分析的に取得し、 L-BFGSなどの数値的手法を使用して最適化するのは簡単です。

最初に、30分で短いセグメントを確認します。

較正済み

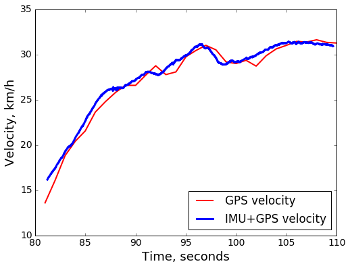
ここでは、どのスケジュールがより正確であるかは明確ではありませんが、2つの異なるソースからの速度推定値が非常に近い補正パラメーターをキャリブレーションが選択できたという意味でのみ、成功を宣言できます。ここで、10分ほどの長い録音で同じアプローチを試してみましょう。

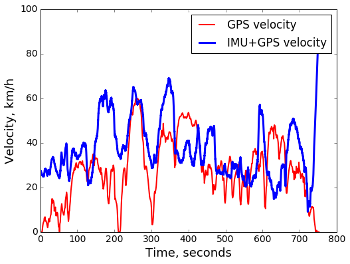
何かがうまくいかなかった

もちろん、完全な失敗があります。単純な補正のモデルは、長い時間間隔に対して不十分であることがわかります。つまり、考慮に入れない重要な歪みの原因があります。かもしれない

ジャイロスコープの系統的エラー（「出発」）。
加速度計とジャイロスコープの累積ホワイトノイズ 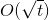$O（\ sqrt {t}）$ 中心極限定理によって。
運転時のエンジン振動との相互作用（車体を介した）。

スライディングウィンドウによるローカル自動キャリブレーション

慣性センサーの単純な補正モデルの問題に対処する方法はたくさんあります。可能なオプション：

原因不明のエラーソース（ジャイロスコープの逸脱、ホワイトノイズの蓄積）をモデリングすることにより、精度を向上させます。
チート。

不正行為です。実際、最終的には、キャリブレーションモデル自体ではなく、最終的な速度値に関心があります。キャリブレーションが短いセグメントに対応している場合、スライディングウィンドウで標準のトリックを使用できます。

全時間間隔を重複する短いセグメントに分割し、
各セグメントで個別にキャリブレーションし、統合により速度を計算します。
それを含むセグメントの各瞬間の結果を平均します。

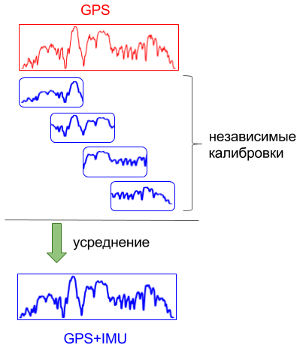
スライディングウィンドウ

最終結果：

最終結果-重なり合うスライディングウィンドウで較正された長距離時系列

前進速度で成功を宣言し、旋回の角速度に戻ります。

コーナースピード

回転角（および、それに応じて、ステアリングホイールの回転角）を計算するには、回転角速度が必要です。 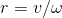$r = v / \オメガ$ 。ジャイロスコープは角速度を直接測定しますが、3次元空間で：垂直軸の周りの回転（ヨー-実際に回転）に加えて、データは横方向（ピッチ-道路勾配の変化、速度バンプの移動）および縦方向（ロール-一方向のチェックイン）わだち掘れやピットへ）：

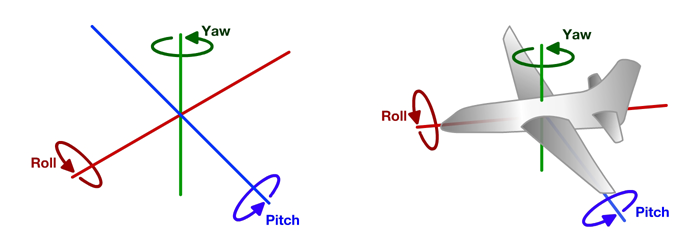
ピッチロールヨー

（車の座標系で）垂直軸の周りのコンポーネントのみを3次元の回転から選択する必要があります。したがって、この軸の方向を取得する必要があります。これを行うには、垂直軸の周りの回転の大きさが縦方向および横方向の周りよりもはるかに大きいという観測を使用します（90度の回転は正常ですが、幸いなことに、勾配と軌道に変化はありません）。そのため、垂直の場合、合計回転が最大であった軸を単純に取得できます。

各基本回転（すなわち、ジャイロスコープの測定）を四元数の形で表示することにより、回転の主軸を数学的に分離するのが便利です。角度による単位軸(x,y,z)

周りの回転 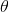$\シータ$ 四元数のようです

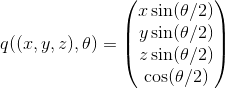
$q（（x、y、z）、\ theta）= \ begin {pmatrix} x \ sin（\ theta / 2）\\ y \ sin（\ theta / 2）\\ z \ sin（\ theta / 2） \\ \ cos（\ theta / 2）\ end {pmatrix}$

便利なのは、クォータニオンの最初の3つのコンポーネントが、回転軸の方向と回転の大きさの両方を同時に特徴付けることです。したがって、主成分法は、クォータニオンの最初の3つの成分に単純に適用される、良い結果をもたらします。支配的な軸を強調表示した後、次の画像が取得されます。

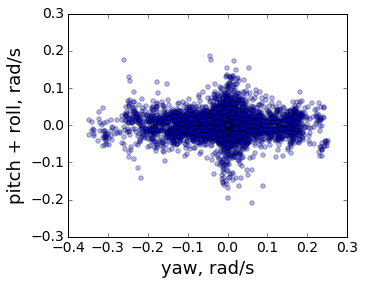
PCA後のローテーション

回転のかなりの割合が、選択された支配的な軸の周りを、それに垂直な他の2つの軸の周りよりも通過していることがわかります。

ちなみに、以前の投稿でも主成分法が使用されていましたが、それを回転に直接適用することは考えていませんでしたが、3次元のパスに沿って水平面を選択しました（つまり、回転ではなく変位に基づいています）。新しい方法は、変位に関する情報を完全に必要としないだけでなく、デバイスの座標系で垂直軸が強調表示されるため、より優れています。つまり、新しいアプローチでは、垂直軸は古いアプローチの軌道全体の中央平面ではなく、道路のローカル平面に垂直になります。たとえば、現在、垂直軸が（上り坂から下り坂に移動するときに車に沿って）回転します。その結果、全回転からの水平回転の割り当てがより正確になりました。

データ

モデルのトレーニングで遊んでみたい人のために、既に処理されたデータにボーナスを共有したいと思います。トレントには、モスクワ近郊の道路に記録された1時間以上の生データに加えて、（ postprocessed

ディレクトリで）並進速度と旋回角速度の計算結果があります。それを使用する場合、結果について知ることは興味深いでしょう！

次のシリーズでは、それだけです。ビデオで制御アクションを予測する方法を学びます。

社内オートパイロット：電話からのセンサーフュージョンとオープントレーニングデータ