問題
測定の永遠の問題は、精度が低いことです。 精度を向上させるには、主に2つの方法があります。1つ目は、測定値に対する感度を上げることですが、原則として、情報価値のないパラメーターに対する感度も向上します。 2番目の方法は、複数の測定値の統計処理で構成されますが、標準偏差は測定値の数の平方根に反比例します。
精度を改善するための統計的方法はさまざまで多数ありますが、測定可能な量が時間とともに変化する場合、静的測定では受動的、動的測定では能動的にも分類されます。 さらに、測定された量自体とノイズは、さまざまな分散を持つランダム変数です。
動的測定の精度を向上させる方法の適応性は、次の測定サイクルの分散と誤差の値を予測することの使用として理解されるべきです。 このような予測は、各測定サイクルで実行されます。 この目的のために、周波数領域で動作するウィナーフィルターが使用されます。 Wienerフィルターとは異なり、Kalmanフィルターは時間で動作し、周波数領域では動作しません。 カルマンフィルターは、多次元問題のために開発され、その定式化はマトリックス形式で実行されます。 マトリックス形式は、記事[1]、[2]でPythonでの実装に十分詳細に説明されています。 これらの記事に記載されているカルマンフィルターの説明は、デジタルフィルターの分野の専門家を対象としています。 したがって、カルマンフィルターの操作をより単純なスカラー形式で考慮することが必要になりました。
理論のビット
離散型のカルマンフィルター回路を考えます。

ここで、G(t)は、その動作が線形関係で記述される単位です。 ブロックの出力で、非ランダム信号y(t)が生成されます。 この信号は、制御対象内で発生するノイズw(t)と加算されます。 この加算の結果、新しい信号x(t)が得られます。 この信号は、非ランダム信号とノイズの合計を表し、ランダム信号です。 さらに、信号x(t)は線形ブロックH(t)によって変換され、w(t)の法則とは異なる分布のノイズv(t)と合計されます。 線形ブロックH(t)の出力で、ランダム信号z(t)を取得します。これにより、非ランダム信号y(t)が決定されます。 ブロックG(t)およびH(t)の線形関数も時間に依存することに注意してください。
ランダムノイズw(t)およびv(t)は、分散Q、R、および数学的な期待値がゼロのランダムプロセスであると仮定します。 ブロックG(t)での線形変換後の信号x(t)は、通常の法則に従って時間的に分布します。 上記に基づいて、測定された信号の比率は次の形式になります。
問題の声明
フィルターの後、非ランダム信号y(t)の可能な最大近似y ''を取得する必要があります。
連続動的測定では、オブジェクトの後続の各状態、したがって制御量の値は、現在の時間間隔で一定の時間Tを持つ指数関数的に前の状態とは異なります
以下は、未知のノイズの多い信号y(t)の方程式を解くPythonプログラムです。 測定プロセスは、それぞれが一様分布の正規分布の関数として形成される2つの擬似ランダム変数の合計と見なされます。
離散適応カルマンフィルターの動作を実証するプログラム
#!/usr/bin/env python #coding=utf8 import matplotlib.pyplot as plt import numpy as np from numpy import exp,sqrt from scipy.stats import norm Q=0.8;R=0.2;y=0;x=0# ( ) . P=Q*R/(Q+R)# . T=5.0# . n=[];X=[];Y=[];Z=[]# . for i in np.arange(0,100,0.2): n.append(i)# . x=1-exp(-1/T)+x*exp(-1/T)# x. y=1-exp(-1/T)+y*exp(-1/T)# y. Y.append(y)# y. X.append(x)# x. norm1 = norm(y, sqrt(Q))# # – y. norm2 = norm(0, sqrt(R))# ))# # – 0. ravn1=np.random.uniform(0,2*sqrt(Q))# # Q. ravn2=np.random.uniform(0,2*sqrt(R))# # R. z=norm1.pdf( ravn1)+norm2.pdf( ravn2)# z. Z.append(z)# z. P=P-(P**2)/(P+Q+R) # x. x=(P*z+x*R)/(P+R)# x. P=(P*R)/(P+R)# x. plt.plot(n, Y, color='g',linewidth=4, label='Y') plt.plot(n, X, color='r',linewidth=4, label='X') plt.plot(n, Z, color='b', linewidth=1, label='Z') plt.legend(loc='best') plt.grid(True) plt.show()
提案されたアルゴリズムとよく知られているアルゴリズムの違いは何ですか
Mathcadのガイドライン[3]に記載されているカルマンフィルターのアルゴリズムを改善しました。
比較された変数x(t)の状態の早すぎる変化の結果、急激な変化の領域のエラーが増加しました。
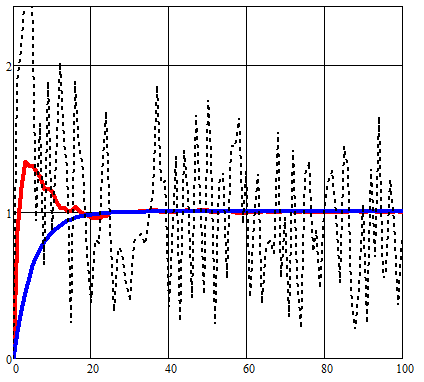
私のアルゴリズムでは、ノイズの影響の初期予測推定値を使用します。 これにより、測定誤差v(t)を減らすことができました。
与えられたアルゴリズムはset-model指数関数を使用します。そのため、明確にするために、カルマンフィルターの一般的なスケジュールでそれらを別々に与えます。
フィルターのグラフィカル分析のためのプログラムコード
#!/usr/bin/env python #coding=utf8 import matplotlib.pyplot as plt import numpy as np from numpy import exp,sqrt from scipy.stats import norm Q=0.8;R=0.2;y=0;x=0# ( ) . P=Q*R/(Q+R)# . T=5.0# . n=[];X=[];Y=[];Z=[]# . for i in np.arange(0,100,0.2): n.append(i)# . x=1-exp(-1/T)+x*exp(-1/T)# x. y=1-exp(-1/T)+y*exp(-1/T)# y. Y.append(y)# y. X.append(x)# x. norm1 = norm(y, sqrt(Q))# # – y. norm2 = norm(0, sqrt(R))# ))# # – 0. ravn1=np.random.uniform(0,2*sqrt(Q))# # Q. ravn2=np.random.uniform(0,2*sqrt(R))# # R. z=norm1.pdf( ravn1)+norm2.pdf( ravn2)# z. Z.append(z)# z. P=P-(P**2)/(P+Q+R) # x. x=(P*z+x*R)/(P+R)# x. P=(P*R)/(P+R)# x. plt.subplot(221) plt.plot(n, Y, color='g',linewidth=2, label=' \n \n ') plt.legend(loc='best') plt.grid(True) plt.subplot(222) plt.plot(n, X, color='r',linewidth=2, label=' \n \n ') plt.legend(loc='best') plt.grid(True) plt.subplot(223) plt.plot(n, Z, color='b', linewidth=1, label=' \n ') plt.legend(loc='best') plt.grid(True) plt.subplot(224) plt.plot(n, Y, color='g',linewidth=2, label='Y') plt.plot(n, X, color='r',linewidth=2, label='X') plt.plot(n, Z, color='b', linewidth=1, label='Z') plt.legend(loc='best') plt.grid(True) plt.show()
プログラムの結果
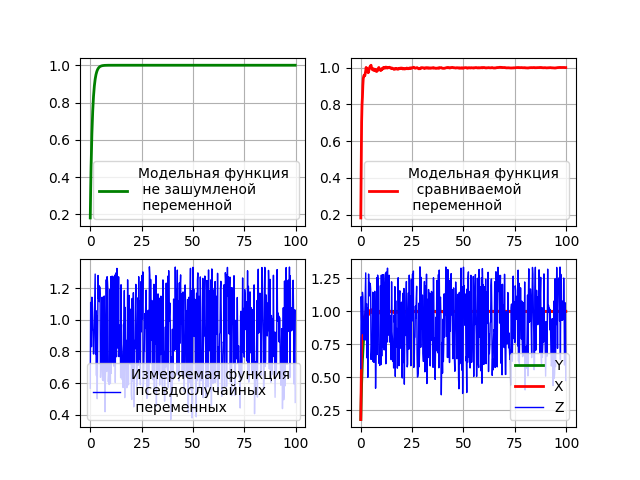
結論
この記事では、条件付きで自由な汎用プログラミング言語Pythonを使用したカルマンフィルターの単純なスカラー実装のモデルについて説明します。これにより、トレーニングの目的でアプリケーションの範囲が拡張されます。