👨🏿‍🤝‍👨🏽 👩🏻‍🎓 📋 Joncker-Volgenantアルゴリズム+ t-SNE =超強度 😧 🀄️ 🎅🏿

宛先：

後：

興味がありますか？しかし、まず最初に。

t-SNE

t-SNEは非常に一般的なアルゴリズムであり、データの次元を小さくして視覚化を容易にします。このアルゴリズムは、データ間の重要な関係を維持しながら、数百の測定値をたった2つにまとめることができます。オブジェクトが元の空間に近いほど、縮小された次元の空間におけるこれらのオブジェクト間の距離は小さくなります。 t-SNEは、小規模および中規模の実データセットで適切に機能し、多数のハイパーパラメーター設定を必要としません。つまり、100,000ポイントを取得して、この魔法のブラックボックスを通過させると、出力に美しい散布図が表示されます。

コンピュータービジョンの分野からの典型的な例を次に示します。 Jan Lekun（エラーの逆伝播法によるニューラルネットワークのトレーニングアルゴリズムの作成者の1人-現代の深層学習の基礎）などによって作成されたMNISTと呼ばれる有名なデータセットがあります。多くの場合、科学的研究だけでなく、ニューラルネットワークに関連するアイデアを評価するための普遍的なデータセットとして使用されます。 MNISTは70,000 28x28の白黒画像です。それらはそれぞれ、セグメント[0、9]からの手書き数字のスキャンです。 MNISTの「無限の」セットを取得する方法はありますが、このトピックから逸脱しません。

したがって、MNISTサンプルには次が含まれます。

$inline$ 署名し、784次元のベクトルとして表すことができます。ベクトルは線形であり、この解釈では個々のピクセル間の位置関係は失われますが、それでも有用です。 784Dでデータセットがどのように見えるかを想像しようとすると、特別な訓練を受けた数学者でないと夢中になります。普通の人は、3D、2D、または1D次元の情報のみを消費できます。暗黙的に、別の次元-時間を追加できますが、3Dコンピューターのディスプレイが100 Hzの周波数で画像を更新するという理由だけで誰かが言うことはほとんどありません。したがって、784個の測定値を2つに表示する方法を知っておくといいでしょう。不可能に聞こえますか？一般的にはそうです。ディリクレの原理が作用します。どのようなマッピングを選択しないか、衝突を避けることはできません。

3Dイリュージョン-> Shadowmaticの 2Dプロジェクション

幸いなことに、次の仮定を立てることができます。

初期の多次元空間は疎です 。つまり、サンプルで均一に満たされることはほとんどありません。
特に存在しないことを知っていれば、正確なマッピングを見つける必要はありません。代わりに、保証された正確な解を持ち、期待される結果を近似する別の問題を解決できます。これは、JPEG圧縮の原理を連想させます。結果はまったく同じではありませんが、画像は元の画像と非常によく似ています。

質問が発生します：パラグラフ2で最も近似する問題は何ですか？残念ながら、「最良」というものはありません。次元削減の品質は主観的であり、最終的な目標、およびクラスタリング方法を選択するときによって異なります。

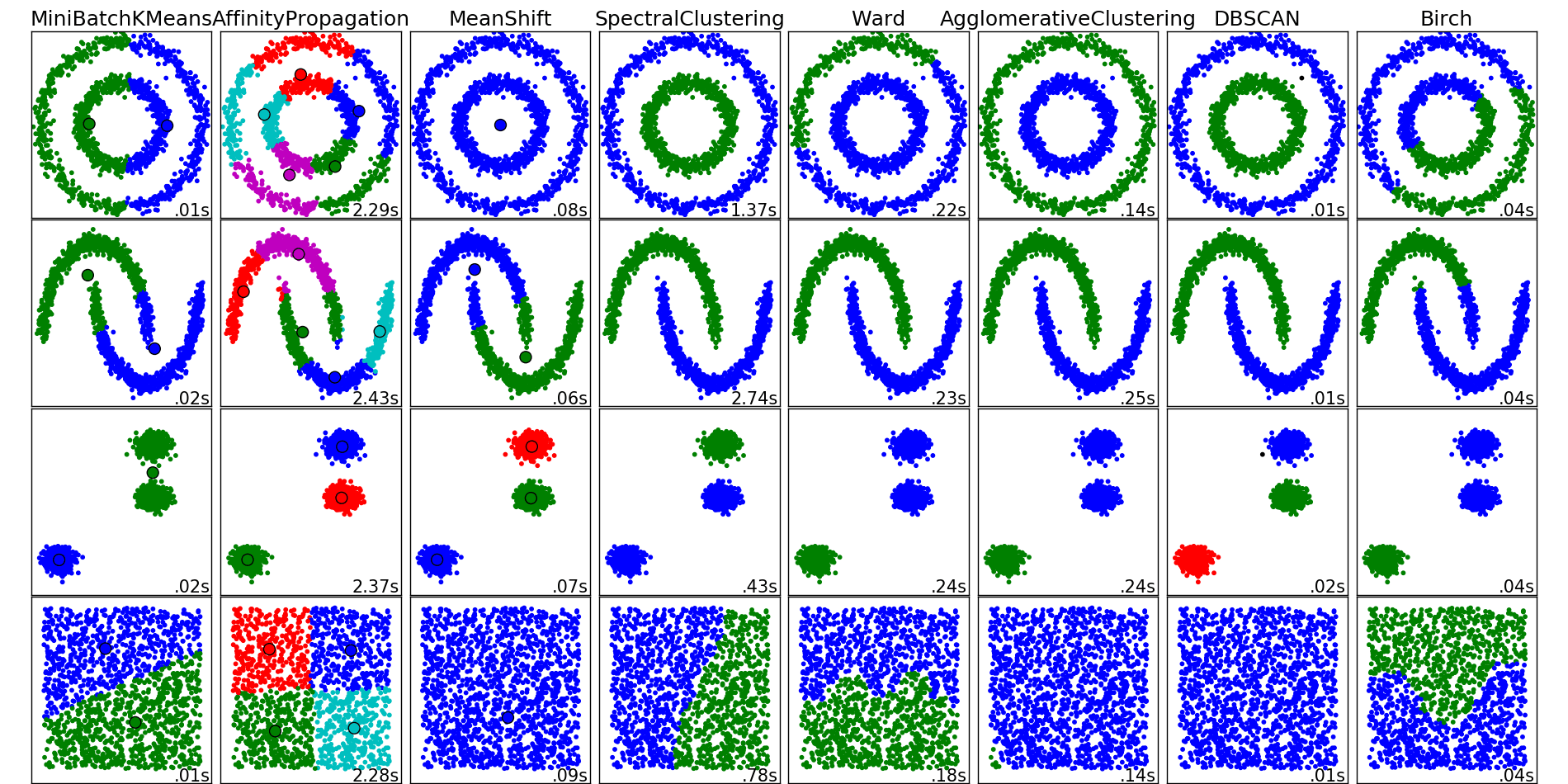
sklearnとは異なるクラスタリングアルゴリズム

t-SNEは、埋め込みグラフアルゴリズムと呼ばれる可能性のある次元削減アルゴリズムの1つです。重要な考え方は、「類似」関係を維持することです。自分で試してみてください。

これらはすべて人工的な例であり、優れていますが、十分ではありません。ほとんどの実際のデータセットは、円錐形のクラスターを持つクラウドに似ています。たとえば、MNISTは次のようになります。

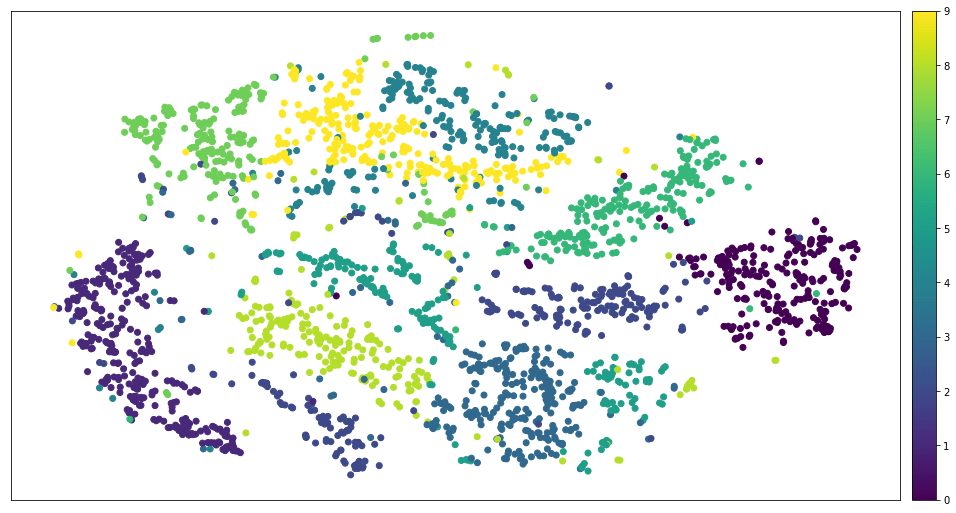
t-SNEを適用した後のMNIST

ラインプログラミング

次に、急に方向を変えて、線形計画法（LP）の概念を理解しましょう。申し訳ありませんが、これは新しいデザインパターン、Javascriptフレームワーク、またはスタートアップではありません。これは数学です：

a r g m i n v e c c c d o t v e c x t a g 1

$\ arg \ min \ vec {c} \ cdot \ vec {x} \ tag {1}$

A c d o t v e c x l e v e c b t a g 2

$A \ cdot \ vec {x} \ le \ vec {b} \ tag {2}$

v e c x g e 0 \タ グ 3

$\ vec {x} \ ge0 \タグ{3}$

スカラー積を最小化します

v e c c

$\ vec {c}$ そして

v e c x

$\ vec {x}$ に依存する線形不等式のシステムを考慮する

v e c x

$\ vec {x}$ 、およびそのすべての座標が負ではないという要件。 LPは、凸最適化の理論でよく研究されているトピックです。ご存知のように、この問題は弱多項式時間で解決できます-通常は

O （ n^{3} ）

$O（n ^ 3）$ 、ここでnは変数の数（タスクディメンション）です。しかし、線形時間で実行される近似アルゴリズムがあります。これらのアルゴリズムは行列乗算を使用し、効果的に並列化できます。プログラマーの楽園！

驚くほど多くのタスクをLPに減らすことができます。たとえば、輸送の問題を考えてみましょう。

輸送タスク：出発点（S）および消費点（D）

出発点と消費点は等しくない場合があります。消費の各ポイントには、一定量の商品が必要です。各出発地点には限られたリソースがあり、いくつかの消費地点に関連付けられています。主なタスクは次のとおりです。各エッジ

C_{i} D_{j}

$C_iD_j$ その価値がある

c_{i j}

$c_ {ij}$ したがって、最小限のコストで供給の分布を見つける必要があります。

厳密に言えば

a r g m i n s u m_{i = 1}^{S} s u m_{j = 1}^{D} x_{i j} c_{i j} \タ グ 4

$\ arg \ min \ sum_ {i = 1} ^ S \ sum_ {j = 1} ^ Dx_ {ij} c_ {ij} \タグ{4}$

x_{i j} g e 0 、 \タ グ 5

$x_ {ij} \ ge0、\タグ{5}$

s u m_{j = 1}^{D} x_{i j} l e w_{S_{i}} 、 t a g 6

$\ sum_ {j = 1} ^ Dx_ {ij} \ le w_ {S_i}、\ tag {6}$

s u m_{i = 1}^{S} x_{i j} l e w_{D_{j}} 、 t a g 7

$\ sum_ {i = 1} ^ Sx_ {ij} \ le w_ {D_j}、\ tag {7}$

s u m_{i = 1}^{S} s u m_{j = 1}^{D} x_{i j} = m i n （ s u m_{i = 1}^{S} w_{S_{i}} 、 s u m_{j = 1}^{D} w_{D_{j}} ） 。 \タ グ 8

$\ sum_ {i = 1} ^ S \ sum_ {j = 1} ^ Dx_ {ij} = \ min（\ sum_ {i = 1} ^ Sw_ {S_i}、\ sum_ {j = 1} ^ Dw_ {D_j }）。 \タグ{8}$

最後の条件は、出発点で商品が終了するか、商品の需要がなくなることを意味します。もし

s u m_{i = 1}^{S} w_{S_{i}} = s u m_{j = 1}^{D} w_{D_{j}}

$\ sum_ {i = 1} ^ Sw_ {S_i} = \ sum_ {j = 1} ^ Dw_ {D_j}$ 、式8は次のように正規化および簡略化できます。

s u m_{i = 1}^{S} s u m_{j = 1}^{D} x_{i j} = s u m_{i = 1}^{S} w_{S_{i}} = s u m_{j = 1}^{D} w_{D_{j}} = 1 。

$\ sum_ {i = 1} ^ S \ sum_ {j = 1} ^ Dx_ {ij} = \ sum_ {i = 1} ^ Sw_ {S_i} = \ sum_ {j = 1} ^ Dw_ {D_j} = 1 。$

「出荷」と「消費」を「土地」に置き換えると、

m i n s u m_{i = 1}^{S} s u m_{j = 1}^{D} x_{i j} c_{i j}

$\ min \ sum_ {i = 1} ^ S \ sum_ {j = 1} ^ Dx_ {ij} c_ {ij}$ ムーバーのタスク（ Earth Mover's Distance 、EMD）に私たちを導きます：あるセットのヒープから別のセットに地球をドラッグするために必要な作業を最小限に抑えます。これで、地面に穴を掘る必要がある場合の対処方法がわかりました。

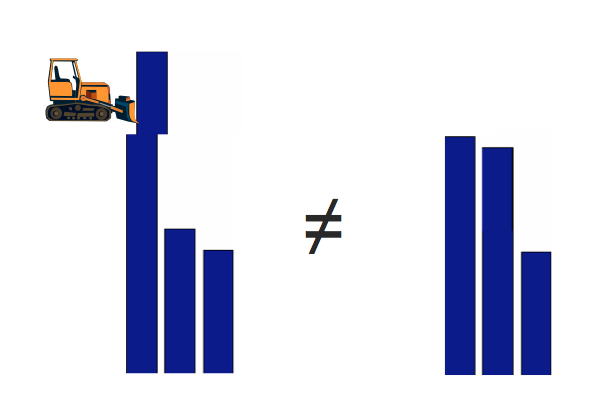
アースムーバーの距離

「出発」と「消費」を「ヒストグラム」に置き換えると、「ディープラーニング前」の時代の画像を比較する最も一般的な方法が得られます（記事例）。この方法は、絶対値の違いだけでなく、場所の違いも考慮するため、単純なL2よりも優れています。

EMDは、ユークリッド距離よりもヒストグラムの比較で優れています

「出発」と「消費」を単語に置き換えると、 word Mve 's Distanceに到達します。これは、 word2vecを使用して単語のベクトル表現を取得する2つの文の意味を比較する効果的な方法です。

ワードムーバーの距離。

条件5〜8を緩和し、 8を投げて、

w_{S_{i}} = w_{D_{i}} = 1

$w_ {S_i} = w_ {D_i} = 1$ 不等式6と7を方程式に変換し、それらに対称な不等式を追加すると、線形割り当て問題LAPが得られます。

a r g m i n s u m_{i = 1}^{S} s u m_{j = 1}^{D} x_{i j} c_{i j} \タ グ 9

$\ arg \ min \ sum_ {i = 1} ^ S \ sum_ {j = 1} ^ Dx_ {ij} c_ {ij} \タグ{9}$

x_{i j} g e 0 、 \タ グ 10

$x_ {ij} \ ge0、\タグ{10}$

s u m_{j = 1}^{D} x_{i j} = 1 、 \タ グ 11

$\ sum_ {j = 1} ^ Dx_ {ij} = 1、\タグ{11}$

s u m_{i = 1}^{S} x_{i j} = 1 \タ グ 12

$\ sum_ {i = 1} ^ Sx_ {ij} = 1 \タグ{12}$

輸送の問題とは対照的に、我々はそれを証明することができます

x_ {ij} \ in \ {0,1 \}

$x_ {ij} \ in \ {0,1 \}$ -ソリューションは常にバイナリです。言い換えれば、出発地からのすべての商品が消費地に行くか、どこにも行きません。

t-SNEラップ

最初のセクションから理解したように、t-SNEは、平面上のすべてのアルゴリズムと同様に、出力に散乱図を生成します。これはデータセットを調査するタスクには理想的ですが、元の図を正しいグリッドに配置する必要がある場合があります。たとえば、このようなスタイリングはソース{d}に必要です...理由はすぐにわかります。

正しいグリッド

ドットの代わりにt-SNEを適用した後、MNISTの数値を示します。これはどのように見えるかです：

t-SNEの後のMNIST数字

あまり明確ではありません。ここで、LAPが発生します。t-SNEサンプルとグリッドノード間のユークリッド距離のペアとしてコストマトリックスを定義し、グリッドエリアをデータセットのサイズに設定します。

| | S | | = | | D | |

$|| S || = || D ||$ 、そしてその結果、問題を解決します。しかし、どのように？アルゴリズムについてはまだ話していません。

Joncker-Volgenantアルゴリズム

シンプレックス法で始まり、非常に複雑なツールで終わる汎用の線形最適化アルゴリズムが非常に多数あることがわかります。特定のタスク用に特別に設計されたアルゴリズムは、いくつかの制限がありますが、通常、はるかに高速に収束します。

ハンガリーのアルゴリズムは、1950年代に開発された特殊な方法の1つです。その複雑さは

O （ n^{3} ）

$O（n ^ 3）$ 。理解と実装が非常に簡単であるため、多くのプロジェクトで人気があります。たとえば、彼は最近sipyの一部になりました。残念ながら、大量のデータでは高速に動作せず、scipyオプションは特に低速です。 2500時間のMNISTサンプルを処理するのに1時間待ちましたが、Pythonはまだ被害者を消化していました。

Jonker-Volgenant（JV）アルゴリズムは、1987年に開発された改良されたアプローチです。また、最短の拡張回路の通過に基づいており、その複雑さもキュービックですが、いくつかのトリックを使用して計算負荷を劇的に削減します。 JVを含む多くのグラフ作成アルゴリズムのパフォーマンスは、 Discrete Applied Mathematicsによる2000年の記事で広範に検討されました。結論は次のとおりです。

「JVはすべてのクラス（タスク-著者注）で良好で安定した平均パフォーマンスを備えており、これはランダムタスクと特定タスクの両方に最適なアルゴリズムです。」

ただし、JVには欠点もあります。彼は、コストマトリックス内の要素のペアの違いに非常に寛容です。たとえば、ダイクストラアルゴリズムを使用してグラフで最短パスを検索し、このグラフに非常に類似した2つのコストが表示される場合、アルゴリズムは無限ループに入るリスクを負います。ダイクストラのアルゴリズムをよく見ると、浮動小数点値の精度の限界に達すると、ひどいことが起こることがわかります。通常の方法は、コストマトリックスに大きな数を掛けることです。

それにもかかわらず、私のような怠け者のエンジニアにとってJVで最も魅力的なのはPython 2パッケージです。これはC： pyLAPJVのアルゴリズムの古代の実装のラッパーです。このCコードは、1996年にMagicLogic OptimizationのためにRoy Jonkerによって書かれました。 pyLAPJVがサポートされなくなったという事実に加えて、プルリクエスト＃2で修正した小さなデータ出力の問題があります。 Cコードは信頼できますが、マルチスレッドまたはSIMD命令を使用しません。もちろん、JVは本質的にシングルスレッドであり、並列化するのはそれほど簡単ではないことを理解していますが、 AVX2を使用して、最も高価なステージ（拡張チェーンの切断）を最適化して、ほぼ2倍高速化しました。その結果、Python 3のsrc-d / lapjvパッケージがMITライセンスの下で利用可能になりました。

拡張チェーンの削減は、基本的に配列内の最小要素と2番目の最小要素を見つけることです。単純に聞こえますが、実際には、最適化されていないCコードは20行かかります。 AVXバージョンは4倍大きくなっています。各SIMDプロセッサエレメントに最小値を送信し、ブレンドを実行してから、SamsungのlibSoundFeatureExtractionで作業中に学んだ他のSIMDブラックマジックスペルを適用します。

template <typename idx, typename cost> __attribute__((always_inline)) inline std::tuple<cost, cost, idx, idx> find_umins( idx dim, idx i, const cost *assigncost, const cost *v) { cost umin = assigncost[i * dim] - v[0]; idx j1 = 0; idx j2 = -1; cost usubmin = std::numeric_limits<cost>::max(); for (idx j = 1; j < dim; j++) { cost h = assigncost[i * dim + j] - v[j]; if (h < usubmin) { if (h >= umin) { usubmin = h; j2 = j; } else { usubmin = umin; umin = h; j2 = j1; j1 = j; } } } return std::make_tuple(umin, usubmin, j1, j2); }

2つの連続した最小値、C ++を見つける

コードを表示

 template <typename idx> __attribute__((always_inline)) inline std::tuple<float, float, idx, idx> find_umins( idx dim, idx i, const float *assigncost, const float *v) { __m256i idxvec = _mm256_setr_epi32(0, 1, 2, 3, 4, 5, 6, 7); __m256i j1vec = _mm256_set1_epi32(-1), j2vec = _mm256_set1_epi32(-1); __m256 uminvec = _mm256_set1_ps(std::numeric_limits<float>::max()), usubminvec = _mm256_set1_ps(std::numeric_limits<float>::max()); for (idx j = 0; j < dim - 7; j += 8) { __m256 acvec = _mm256_loadu_ps(assigncost + i * dim + j); __m256 vvec = _mm256_loadu_ps(v + j); __m256 h = _mm256_sub_ps(acvec, vvec); __m256 cmp = _mm256_cmp_ps(h, uminvec, _CMP_LE_OQ); usubminvec = _mm256_blendv_ps(usubminvec, uminvec, cmp); j2vec = _mm256_blendv_epi8( j2vec, j1vec, reinterpret_cast<__m256i>(cmp)); uminvec = _mm256_blendv_ps(uminvec, h, cmp); j1vec = _mm256_blendv_epi8( j1vec, idxvec, reinterpret_cast<__m256i>(cmp)); cmp = _mm256_andnot_ps(cmp, _mm256_cmp_ps(h, usubminvec, _CMP_LT_OQ)); usubminvec = _mm256_blendv_ps(usubminvec, h, cmp); j2vec = _mm256_blendv_epi8( j2vec, idxvec, reinterpret_cast<__m256i>(cmp)); idxvec = _mm256_add_epi32(idxvec, _mm256_set1_epi32(8)); } float uminmem[8], usubminmem[8]; int32_t j1mem[8], j2mem[8]; _mm256_storeu_ps(uminmem, uminvec); _mm256_storeu_ps(usubminmem, usubminvec); _mm256_storeu_si256(reinterpret_cast<__m256i*>(j1mem), j1vec); _mm256_storeu_si256(reinterpret_cast<__m256i*>(j2mem), j2vec); idx j1 = -1, j2 = -1; float umin = std::numeric_limits<float>::max(), usubmin = std::numeric_limits<float>::max(); for (int vi = 0; vi < 8; vi++) { float h = uminmem[vi]; if (h < usubmin) { idx jnew = j1mem[vi]; if (h >= umin) { usubmin = h; j2 = jnew; } else { usubmin = umin; umin = h; j2 = j1; j1 = jnew; } } } for (int vi = 0; vi < 8; vi++) { float h = usubminmem[vi]; if (h < usubmin) { usubmin = h; j2 = j2mem[vi]; } } for (idx j = dim & 0xFFFFFFF8u; j < dim; j++) { float h = assigncost[i * dim + j] - v[j]; if (h < usubmin) { if (h >= umin) { usubmin = h; j2 = j; } else { usubmin = umin; umin = h; j2 = j1; j1 = j; } } } return std::make_tuple(umin, usubmin, j1, j2); }

AVX2命令を使用して最適化された2つの連続した最小値を見つける

私のラップトップでは、lapjvが2500のMNISTサンプルを5秒でパックします。ここにあります-貴重な結果：

t-SNE後のMNISTの割り当て割り当て

ノートブック

この投稿を準備するために、私はJupiter Notebookを使用しました（ソースはこちら）。

おわりに

t-SNEで処理したサンプルを正しいグリッドに置く効果的な方法があります。 src-d / lapjvで実装されたJonker-Volgenantアルゴリズムを使用して、割り当て問題（LAP）を解決することに基づいています。このアルゴリズムは、10,000サンプルまでスケーリングできます。

ああ、仕事に来てくれませんか？ :)
wunderfund.ioは、高頻度アルゴリズム取引を扱う若い財団です。高頻度取引は、世界中の最高のプログラマーと数学者による継続的な競争です。私たちに参加することで、あなたはこの魅力的な戦いの一部になります。

熱心な研究者やプログラマー向けに、興味深く複雑なデータ分析と低遅延の開発タスクを提供しています。柔軟なスケジュールと官僚主義がないため、意思決定が迅速に行われ、実施されます。

チームに参加： wunderfund.io

Joncker-Volgenantアルゴリズム+ t-SNE =超強度