デジタル信号処理に関する書籍や出版物は、開発者が直面しているタスクを知らず、理解していないことが多い著者によって書かれています。 これは特にリアルタイムシステムに当てはまります。 これらの著者は、時間と空間の外に存在する神のささやかな役割を自分自身に割り当てます。 この出版物は、ほとんどの開発者が抱えている困惑を払拭し、「エントリのしきい値」を克服するのを支援することを目的としています。これらの目的のために、テキストは意図的にプログラミング領域のアナロジーと用語を使用しています。
この作品は、完全で接続されていることを意味するものではありません。
コメントを読んだ後に追加されました。
FFTの実行方法に関する出版物は明らかに十分ではありませんが、FFTの作成、スペクトルの変換、および信号の再収集をリアルタイムで行う方法です。 著者はこのギャップを埋めようとしています。
パート1、概要
離散線形動的システムを構築する主な方法は2つあります。 文献では、このようなシステムは一般にデジタルフィルターと呼ばれ、2つの主なタイプに分類されます。有限インパルス応答(FIR)フィルターと無限インパルス応答(IIR)フィルターです。
FIRフィルターのアルゴリズムの本質は、畳み込み積分の離散計算にあります。

ここで、x(t)は入力信号です
y(t)-出力信号
h(t)は、フィルターのインパルス応答またはデルタ関数に対するフィルターの応答です。 インパルス応答は、フィルターK(f)の複素周波数応答の逆フーリエ変換です。
読者にわかりやすい図を作成するために、C言語の畳み込み積分をリアルタイムで離散的に計算する例を示します。
#define L (4) // int FIR(int a) { static int i=0; // static int reg[L]; // static const int h[L]={1,1,1,1};// int b=0;// reg[i]=a; // for(int j=0;j<L;j++)// { b=b+h[j]*reg[i]; i=(i-1)&(L-1); } i=(i+1)&(L-1);// return b; }
特定の時間間隔Tでこの関数を呼び出し、入力信号を引数として渡すことにより、出力で、次の形式のインパルス応答でのフィルターの反応に対応する出力信号を取得します。
0 <t <4Tの場合、h(t)= 1
h(t)= 0その他の場合。
このようなインパルス応答を備えたフィルタは、「移動平均フィルタ」という名前で収集されたすべての人によく知られているため、はるかに簡単に実装できます。 この場合、そのようなインパルス応答が例として使用されます。
FIRフィルターのインパルス特性の合成に関する多くの文献がありますが、望ましい特性を持つフィルターを取得するための既製のソフトウェア製品もあります。 著者は、Matlabパッケージのバグの多いフィルター設計ツールを好みますが、これは好みの問題です。
有限インパルス応答を持つフィルターを使用すると、実際には有限インパルス応答を持つ動的システムは存在しないため、通常の現実を少し上回ることができます。 FIRフィルターは、自然の流れではなく、反対側から時間周波数領域に入力しようとするため、これらのフィルターの周波数特性には多くの場合、予期しない特性があります。
無限インパルス応答を持つフィルターは、自然に非常に近いものです。 無限インパルス応答を持つフィルターのアルゴリズムの本質は、再帰的(再帰的と混同しないように!)に削減されます。フィルターを記述する微分方程式の解。 つまり、フィルター出力信号の後続の各値は、前の値に基づいて計算されます。 これが、現実世界のプロセスの進め方です。 毎秒超高層ビルから落下する石は、その速度を9.8m / s増加させます。速度=速度+ 9.8で、毎秒移動する距離は距離=距離+速度を増加させます。 これが再帰的なアルゴリズムではないと言う人は誰でも、最初の人に石を投げさせてください。 Matrixでのみ、石の位置を返す関数を呼び出すための時間間隔は、利用可能な測定器の分割価格よりもはるかに小さくなります。
また、「フィルター次数」の概念を定義したいと思います。 これは、再帰的操作を受ける変数の数です。 この例では、石の速度を返す関数は1次であり、移動したパスを返す関数は2次です。
読者の最終的な啓発のために、「指数平滑法フィルター」として一般に知られる最も単純なローパスフィルターの言語Cの例を示します。
#define alfa (2) // int filter(int a) { static int out_alfa=0; out_alfa=out_alfa - (out_alfa >>alfa) + a; return (out_alfa >> alfa); }
この関数を周波数Fで呼び出し、入力信号を引数として渡すことにより、出力で、カットオフ周波数を持つ1次ローパスフィルターの反応に対応する出力信号を取得します。
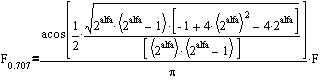
与えられたソースコードの例は、アルゴリズムの本質を理解するという観点からは完全に消化できません。 アルゴリズムの反復的な性質(「ストーンフォール」を参照)の観点からは、y = y +((xy)>> alfa)よりも正確ですが、この場合、alfaは有効数字を失います。 サンプルコードからの再帰フィルター式は、重要なビットの損失を回避するような方法で構築されます。 無限インパルス応答を備えたデジタルフィルターの美しさを損なう可能性があるのは、計算の究極の精度です。 これは、高品質係数を特徴とする高次フィルターで特に顕著です。 実際の動的システムでは、このような問題は発生せず、 マトリックスは驚くほど正確に計算を実行します。
多くの文献がそのようなフィルターの合成に捧げられています;既製のソフトウェア製品もあります(上記参照)。
パート2 フーリエフィルター
大学のコース(あなたの従順な召使がこのOTECコースを受講しました)の多くは、線形動的システムの分析に対する2つの主なアプローチを覚えています。時間領域での分析と周波数領域での分析です。 時間領域解析は、微分方程式、畳み込み、およびデュアメル積分の解です。 これらの分析方法は、IIRおよびFIRデジタルフィルターに個別に組み込まれています。
しかし、線形動的システムの解析には周波数アプローチがあります。 演算子と呼ばれることもあります。 使用される演算子は、フーリエ変換、ラプラス変換などです。 さらに、フーリエ変換についてのみ説明します。
この分析方法は、デジタルフィルターの構築には広く使用されていません。 著者は、ロシア語でそのようなフィルターを構築するための健全な実用的な推奨事項を見つけることができませんでした。 実用的な文献でそのようなフィルターについて簡単に言及しているのは[Rabiner L.、Gould B.、Theory and Application of Digital Signal Processing 1978]だけですが、この本ではそのようなフィルターの検討は非常に表面的です。 この本では、このフィルター構成スキームは「FFTメソッドを使用したリアルタイムコンボリューション」と呼ばれます。私の控えめな意見では、本質をまったく反映していないため、名前は短くする必要があります。
線形動的システムの応答は、複素伝達係数K(f)の入力フーリエ画像x(t)の積の逆フーリエ変換です。
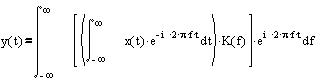
実際には、この分析式は次の手順を前提としています。入力信号のフーリエ変換を行い、結果に複素伝達係数を乗算し、結果を出力信号とする逆フーリエ変換を実行します。 実際の離散時間では、この手順は実行できません。 時間積分をマイナスからプラス無限に取る方法 時間外にしか取れない...
離散世界では、フーリエ変換を実装するためのツールがあります-高速フーリエ変換(FFT)アルゴリズム。 フーリエフィルターを実装するときに使用します。 FFT関数の引数は、2 ^ n要素の時間サンプルの配列です。2^ n要素の2つの配列の結果は、フーリエ変換の実数部と虚数部に対応します。 FFTアルゴリズムの離散的な特徴は、入力信号が2 ^ nの間隔で周期的と見なされることです。 これにより、フーリエフィルターアルゴリズムにいくつかの制限が課せられます。 入力信号のサンプルのシーケンスを取得し、それらからFFTを描画し、FFT結果に複素フィルターゲインを乗算して逆変換を実行すると、 何も機能しません! 出力信号には、サンプルの接合部付近に大きな非線形歪みがあります。
この問題を解決するには、2つの方法を適用する必要があります。
- 1.サンプルは、オーバーラップのあるフーリエ変換で処理する必要があります。 つまり、後続の各選択には前の選択の一部が含まれている必要があります。 理想的には、サンプルは(2 ^ n-1)サンプルでオーバーラップする必要がありますが、これには膨大な計算コストが必要です。 実際には、4分の3(2 ^ n-2 ^(n-2))、半分(2 ^(n-1))、さらには4分の1のオーバーラップ(2 ^(n-2))で十分です。
- 2.出力信号を得るために、逆フーリエ変換の結果は、互いに重ね合わせる前に、重み関数(重み係数の配列)で乗算する必要があります。 重み関数は、次の条件を満たす必要があります。
- 2.1間隔2 ^ nを除くすべての場所でゼロに等しい。
- 2.2間隔の端でゼロになる傾向があります。
- 2.3そして、最も重要なこととして、オーバーラップ間隔kだけシフトされた重み関数Fv(t)の合計は一定でなければなりません。

このような関数は、デジタル信号処理の技術で広く使用されており、それらをウィンドウと呼ぶことが慣習となっています。 著者のささやかな意見によると、実用的な観点からのベストはカーンウィンドウです。
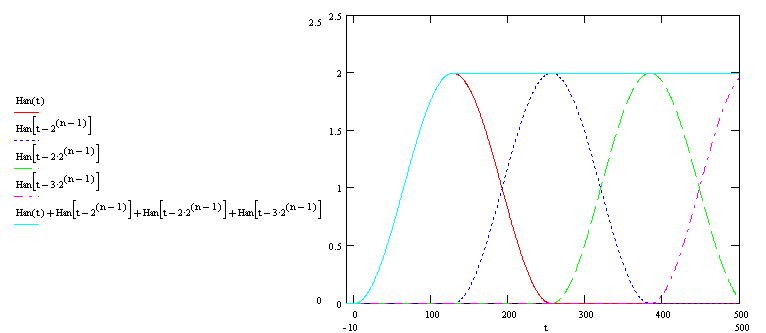
図は、カーンウィンドウ2 ^ n = 256の長さのプロパティを示すグラフです。 ウィンドウインスタンスは、半分のオーバーラップk = 128で構築されます。 ご覧のとおり、上記のプロパティはすべて使用可能です。
労働者の要求により、次の図はサンプル長が2 ^ n = 8のフーリエフィルターの計算スキームを示しています。サンプル数は3です。計算プロセスをそのような図に表示するのは非常に難しく、その周期性を示すことは特に難しいため、サンプル数を3に制限しました。

入力信号は50%のオーバーラップでブロック2 ^ n = 8に分割され、各ブロックからFFTが取得され、FFTの結果に必要な変換が行われ、逆FFTが実行され、逆FFTの結果にウィンドウがスカラー乗算されます。乗算後、ブロックにオーバーラップが追加されます。
スペクトル変換を実行する場合、実信号のFFT配列の主な特性を忘れないでください。FFT配列の前半は後半と複雑に結合します。つまり、Re [i] = Re [(1 << n)-i]); Im [i] =-Im [(1 << n)-i]);。 これらの要件が満たされない場合、出力信号は単に「組み立てられません」。
これで、フーリエフィルターアルゴリズムの記述に必要なすべてがわかりました。 Cでアルゴリズムを説明します。
#include <math.h> #define FSempl (8000)// #define BufL (64) // #define Perk (2) // 2-1/2, 4-3/4 // , #define FsrLow (300)// #define FsrHi (3100)// #define FsrLowN ((BufL*FsrLow+(FSempl/2))/FSempl)// #define FsrHiN ((BufL*FsrHi +(FSempl/2))/FSempl)// // #define SdvigSp (0)// +() -() 0( ) // , #define FilterSpekrtaT_EN (1)// 1/0 #define FiltSpektrFsr (0.100025f) // volatile unsigned short ShBuf;// signed short BufIn[BufL*2];// signed short BufOut[BufL*2];// signed short BufInOut[BufL];// float FurRe[BufL];// float FurIm[BufL];// #if (FilterSpekrtaT_EN!=0) float FStektr[BufL/2];// #endif // #if BufL==64 const float SinCosF[]= { 0.000000000 , 0.098017140 , 0.195090322 , 0.290284677 , 0.382683432 , 0.471396737 , 0.555570233 , 0.634393284 , 0.707106781 , 0.773010453 , 0.831469612 , 0.881921264 , 0.923879533 , 0.956940336 , 0.980785280 , 0.995184727 , 1.000000000 , 0.995184727 , 0.980785280 , 0.956940336 , 0.923879533 , 0.881921264 , 0.831469612 , 0.773010453 , 0.707106781 , 0.634393284 , 0.555570233 , 0.471396737 , 0.382683432 , 0.290284677 , 0.195090322 , 0.098017140 , 0.000000000 , -0.098017140, -0.195090322, -0.290284677, -0.382683432, -0.471396737, -0.555570233, -0.634393284, -0.707106781, -0.773010453, -0.831469612, -0.881921264, -0.923879533, -0.956940336, -0.980785280, -0.995184727, -1.000000000, -0.995184727, -0.980785280, -0.956940336, -0.923879533, -0.881921264, -0.831469612, -0.773010453, -0.707106781, -0.634393284, -0.555570233, -0.471396737, -0.382683432, -0.290284677, -0.195090322, -0.098017140, 0.000000000 , 0.098017140 , 0.195090322 , 0.290284677 , 0.382683432 , 0.471396737 , 0.555570233 , 0.634393284 , 0.707106781 , 0.773010453 , 0.831469612 , 0.881921264 , 0.923879533 , 0.956940336 , 0.980785280 , 0.995184727 }; #endif // #if BufL==64 const unsigned short sortFFT[]= { 0x0000,0x0020,0x0010,0x0030,0x0008,0x0028,0x0018,0x0038, 0x0004,0x0024,0x0014,0x0034,0x000C,0x002C,0x001C,0x003C, 0x0002,0x0022,0x0012,0x0032,0x000A,0x002A,0x001A,0x003A, 0x0006,0x0026,0x0016,0x0036,0x000E,0x002E,0x001E,0x003E, 0x0001,0x0021,0x0011,0x0031,0x0009,0x0029,0x0019,0x0039, 0x0005,0x0025,0x0015,0x0035,0x000D,0x002D,0x001D,0x003D, 0x0003,0x0023,0x0013,0x0033,0x000B,0x002B,0x001B,0x003B, 0x0007,0x0027,0x0017,0x0037,0x000F,0x002F,0x001F,0x003F }; #endif // #if BufL==64 const float WinHanF[]= { 0.0 , 0.002407637 , 0.00960736 , 0.021529832 , 0.038060234 , 0.059039368 , 0.084265194 , 0.113494773 , 0.146446609 , 0.182803358 , 0.222214883 , 0.264301632 , 0.308658284 , 0.354857661 , 0.402454839 , 0.45099143 , 0.5 , 0.54900857 , 0.597545161 , 0.645142339 , 0.691341716 , 0.735698368 , 0.777785117 , 0.817196642 , 0.853553391 , 0.886505227 , 0.915734806 , 0.940960632 , 0.961939766 , 0.978470168 , 0.99039264 , 0.997592363 , 1.0 , 0.997592363 , 0.99039264 , 0.978470168 , 0.961939766 , 0.940960632 , 0.915734806 , 0.886505227 , 0.853553391 , 0.817196642 , 0.777785117 , 0.735698368 , 0.691341716 , 0.645142339 , 0.597545161 , 0.54900857 , 0.5 , 0.45099143 , 0.402454839 , 0.354857661 , 0.308658284 , 0.264301632 , 0.222214883 , 0.182803358 , 0.146446609 , 0.113494773 , 0.084265194 , 0.059039368 , 0.038060234 , 0.021529832 , 0.00960736 , 0.002407637 }; #endif //@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@ // // // ReFT ImFT // . void FFTnoInv(float* ReFT,float* ImFT) { // for(int i=0;i<BufL;i++) { int j=sortFFT[i];// if(i<j)// { // float swp=ReFT[i]; ReFT[i]=ReFT[j]; ReFT[j]=swp; // //swp=ImFT[i]; //ImFT[i]=ImFT[j]; //ImFT[j]=swp; } } // long darg=BufL; // for(long LP2=1;LP2!=BufL;LP2=LP2<<1)// { darg=darg>>1; long arg=0; // , for(int j=0;j<LP2;j++) // { float c=(SinCosF[arg+(BufL/4)]);// float s=(SinCosF[arg]);// arg=(arg-darg)&(BufL-1);// for(int i=j;i<BufL;i=(i+LP2+LP2)) // { //!!! float wr=(c*ReFT[i+LP2])-(s*ImFT[i+LP2]); float wi=(s*ReFT[i+LP2])+(c*ImFT[i+LP2]); ReFT[i+LP2]=ReFT[i]-wr; ImFT[i+LP2]=ImFT[i]-wi; ReFT[ i ]=ReFT[i]+wr; ImFT[ i ]=ImFT[i]+wi; } } } // return; } //@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@ // // // ReFT ImFT // . // 0 void FFTInv(float* ReFT,float* ImFT) { // for(int i=0;i<BufL;i++) { int j=sortFFT[i];// if(i<j)// { // float swp=ReFT[i]; ReFT[i]=ReFT[j]; ReFT[j]=swp; swp=ImFT[i]; ImFT[i]=ImFT[j]; ImFT[j]=swp; } } // long darg=BufL;// for(long LP2=1;LP2!=BufL;LP2=LP2<<1)// { darg=darg>>1; long arg=0;//// , for(int j=0;j<LP2;j++)// { float c=(SinCosF[arg+(BufL/4)]);// float s=(SinCosF[arg]);// arg=arg+darg;// for(int i=j;i<BufL;i=(i+LP2+LP2))// { //!!! float wr=(c*ReFT[i+LP2])-(s*ImFT[i+LP2]); float wi=(s*ReFT[i+LP2])+(c*ImFT[i+LP2]); ReFT[i+LP2]=ReFT[i]-wr; ImFT[i+LP2]=ImFT[i]-wi; ReFT[ i ]=ReFT[i]+wr; ImFT[ i ]=ImFT[i]+wi; } } } //, for(int i=0;i<BufL;i++) { ReFT[i]=ReFT[i] * WinHanF[i] * ( (1.0F/((float)BufL)) * (2.0F/((float)Perk)) ); } // return; } //@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@ // void ObrBuf(void) { // for(int i=0;i<(BufL);i++) { FurRe[i]=((float)BufInOut[i]); FurIm[i]=0.0F; } // FFTnoInv(FurRe,FurIm); // #if SdvigSp>0 // , - for(int i=1;i<(BufL/2);i++) { if(i>=(BufL/2-SdvigSp)) { FurRe[i]=FurIm[i]=0; FurRe[BufL-i]=FurIm[BufL-i]=0; continue; } FurRe[i]=FurRe[i+SdvigSp]; FurIm[i]=FurIm[i+SdvigSp]; FurRe[BufL-i]=FurRe[i]; FurIm[BufL-i]=-FurIm[i]; } #endif #if SdvigSp<0 // , for(int i=(BufL/2-1);i>0;i--) { if(i<=(-SdvigSp)) { FurRe[i]=FurIm[i]=0; FurRe[BufL-i]=FurIm[BufL-i]=0; continue; } FurRe[i]=FurRe[i-(-SdvigSp)]; FurIm[i]=FurIm[i-(-SdvigSp)]; FurRe[BufL-i]=FurRe[i]; FurIm[BufL-i]=-FurIm[i]; } #endif // , FurRe[0]=0.0F;FurIm[0]=0.0F; // FurRe[(BufL/2)]=0.0F;FurIm[(BufL/2)]=0.0F;// float ZnStektr[BufL/2];// for(int i=1;i<(BufL/2);i++) { if( ( i < FsrLowN )// || ( i > FsrHiN )// ) { // , FurRe[i]=0.0F;FurIm[i]=0.0F;// FurRe[BufL-i]=0.0F;FurIm[BufL-i]=0.0F;// } else // { ZnStektr[i]=sqrtf(FurRe[i]*FurRe[i])+(FurIm[i]*FurIm[i]);// } } // , for(int i= FsrLowN;// i<=FsrHiN ;// i++) { #if FilterSpekrtaT_EN!=0 // , FStektr[i]=FStektr[i]+ FiltSpektrFsr*(ZnStektr[i]-FStektr[i]); #endif // FurRe[i]=FurRe[BufL-i]=(FStektr[i]*FurRe[i])/ZnStektr[i]; FurIm[i]=(FStektr[i]*FurIm[i])/ZnStektr[i]; FurIm[BufL-i]=-FurIm[i]; } // FFTInv(FurRe,FurIm); // for(int i=0;i<(BufL);i++) { BufInOut[i]=((signed short)(FurRe[i]+0.5f)); } } //@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@ // signed short FureFilter(signed short t1) { // BufIn[ShBuf]=t1; // signed short out=BufOut[ShBuf]; // ShBuf=(ShBuf+1)&((BufL*2)-1); // if((ShBuf&((BufL/Perk)-1))==0) { // int ShTmpOut=ShBuf; int ShTmpIn=(ShBuf-BufL)&((BufL*2)-1); for(int i=0;i<(BufL);i++) { if(i<(BufL-(BufL/Perk))) { // BufOut[ShTmpOut]=BufOut[ShTmpOut]+BufInOut[i]; } else { // BufOut[ShTmpOut]=BufInOut[i]; } // ShTmpOut=(ShTmpOut+1)&((BufL*2)-1); // BufInOut[i]=BufIn[ShTmpIn]; // ShTmpIn=(ShTmpIn+1)&((BufL*2)-1); } }// if((ShBuf&((BufL/Perk)-1))==0) // // ! if((ShBuf&((BufL/Perk)-1))==0)ObrBuf(); return out; }
FSempl周波数でFureFilter()関数を呼び出し、入力信号を引数として渡すと、結果は出力信号になります。 この例では、入力信号は次のように処理されます:信号はカットオフ周波数FsrLow、FsrHiのバンドパスフィルターを通過し、示された周波数の上下のすべてのスペクトル成分が抑制され、信号スペクトルがシフトします(音信号の場合、これはピノキオカラバス効果として認識されます)、信号の振幅スペクトルローパスフィルターによる平滑化が行われます(音の場合、これはエコールームの効果です)。 信号のこれらのアクションは、例として、周波数領域での信号処理の技術的方法を示すために実行されます:係数の複素共役の観察、三角関数を使用せずに振幅から複素スペクトルを復元するなど。
おわりに
ほとんどの場合、このフーリエフィルター関数は実際には動作しないことに注意してください。 この関数を呼び出すとき、8000 Hzの低周波数であっても、次の呼び出しまでに完了する時間はなく、十分な速度がありません。 このフーリエフィルタープログラムコードは、特定のハードウェアリソースを参照せずにアルゴリズムの説明として提供され、純粋に教育的な目標を持っています (「はじめに」を参照)。
実際の実装では、BufInOut []バッファのfill-empty関数(PDPなどをすぐに使用することをお勧めします)とObrBuf()バッファ処理関数の実行を並列化する必要がありますが、これはまったく別の話です。