cvxpyを使用してPythonで簡単な最適化問題を解決する方法

すべての人に良い一日を！ 簡単な検索では、 cvxpyモジュールの言及を見つけることができなかったため、トレーニング資料を作成することにしました。 cvxpyは、最適化の問題を解決するために設計されています-特定の制限を持つ関数の最小/最大を見つけます。 このトピックに興味があるなら、猫をお願いします。

問題の一般的な声明

ここで、 xは独立変数（一般的な場合はベクトル）、 f（x）

最適化される目的関数。 f（x）の定義のドメインの制限は、等式と不等式を使用して指定できます。

タスクの例

次の線形計画問題を見てみましょう。











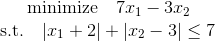
モジュールの不等式によって定義された領域を見ると、この領域は線形不等式を使用して簡単に定義できることがわかります。









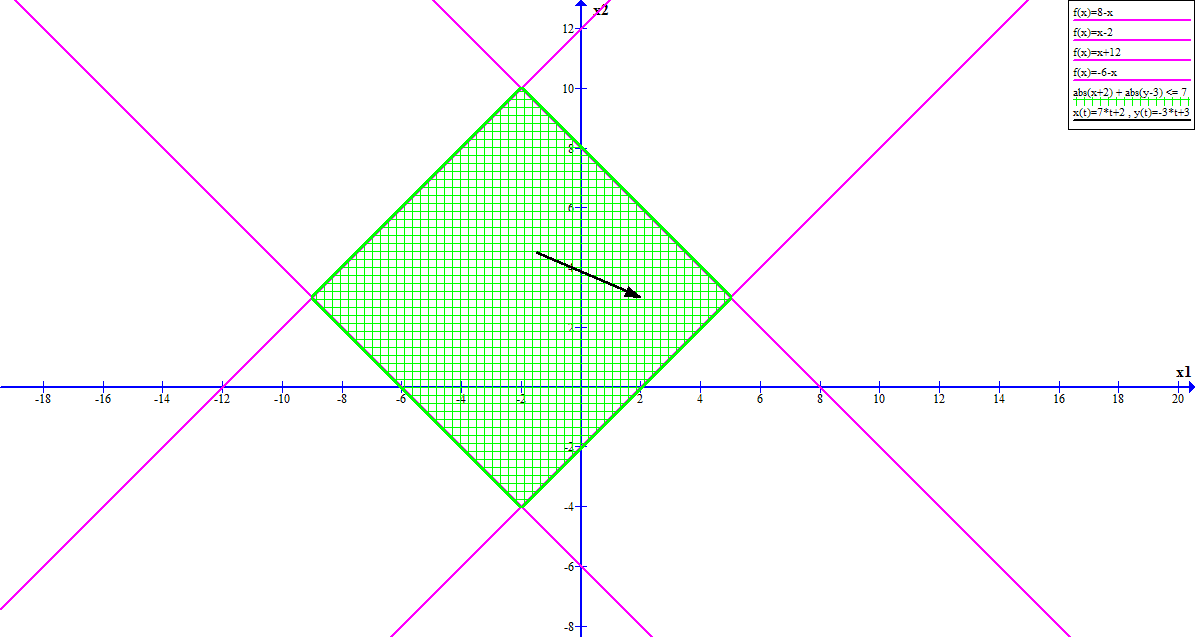
この場合、制限は次のようになります。

cvxpyを使用して問題を解決する

モジュールのインストールについては、モジュールのWebサイトで詳しく説明されています 。 テストの最適化の問題を解決できる簡単なコードを作成しましょう。

import numpy as np import cvxpy as cvx #    x = cvx.Variable(2) A = np.array([[1, 1], [1, -1], [-1, 1], [-1, -1]]) b = np.array([8, 2, 12, 6]) c = np.array([7, -3]) #  constraints = [A * x <= b] #        obj = cvx.Minimize(c * x) #     prob = cvx.Problem(obj, constraints) prob.solve() print(prob.status) # optimal print(prob.value) # -71.999999805 print(x.value) # [[-8.99999997] [ 3.00000002]]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

現在のソリューションは完全ではなく、制限を超えていますが、最適なソリューションの隣にあることがわかります（-9、3） 。 cvxpyでは、さまざまなソルバーを使用して問題を解決し、最適なソルバーを選択できます。 GLPKを試してみましょう：

 prob.solve(solver = "GLPK") print(prob.status) # optimal print(prob.value) # -72.0 print(x.value) # [[-9.] [ 3.]]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

使用可能なソルバーのリストは、 installed_solvers()



関数によって返されます。

他の例

線形計画問題だけでなく解決することも可能です。 問題の最初の声明を見てみましょう。

 #  constraints = [cvx.abs(x[0] + 2) + cvx.abs(x[1] - 3) <= 7] #        obj = cvx.Minimize(c * x) #     prob = cvx.Problem(obj, constraints) prob.solve(solver = "GLPK") print(prob.status) # optimal print(prob.value) # -72.0 print(x.value) # [[-9.] [ 3.]]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

最小二乗法の解決策を探すこともできます：

 #        obj = cvx.Minimize(cvx.norm(A * x - b)) #      #     prob = cvx.Problem(obj) prob.solve() print(prob.status) # optimal print(prob.value) # 13.9999999869 print(x.value) # [[-2.] [ 3.]]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

もちろん、いくつかのタスクには簡単な解決策があります。

 A = np.array([[1, 1], [1, -1], [-1, 1]]) b = np.array([8, 2, 12]) c = np.array([7, -3]) #  constraints = [A * x <= b] #        obj = cvx.Minimize(c * x) #     prob = cvx.Problem(obj, constraints) prob.solve() print(prob.status) # unbounded print(prob.value) # -inf print(x.value) # None
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

また、解決策がない場合もあります。

 A = np.array([[1, 1], [1, -1], [-1, 1], [-1, -1]]) b = np.array([-6, -12, -2, -8]) #  constraints = [A * x <= b] #        obj = cvx.Minimize(c * x) #     prob = cvx.Problem(obj, constraints) prob.solve() print(prob.status) # infeasible print(prob.value) # inf print(x.value) # None
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

以上です。 詳細については、モジュールのWebサイトをご覧ください 。