Clever Geek Handbook

ロックフリーのデータ構造。 イテレータ：マルチレベル配列

opusの前の部分（ 1、2、3 ）では、ロックフリーマップの内部構造を調べ、すべての基本操作（キーの検索、追加、削除）がグローバルロックなしで、さらにはロックフリーな方法でも実行できることを確認しました。 しかし、標準のstd::map



は、別の非常に便利な抽象化-イテレータをサポートしています。 反復可能なロックフリーマップを実装することは可能ですか？

この質問への答えは控えめです。



一年前、私は原則として、ロックフリーのコンテナにはイテレータが実行可能ではないと確信していました。 自分で判断してください：イテレータを使用すると、コンテナのすべての要素をバイパスできます。 しかし、ロックフリーの世界では、コンテナの内容は常に変化しているので、「すべての要素をバイパスする」と考えられるものは何ですか？







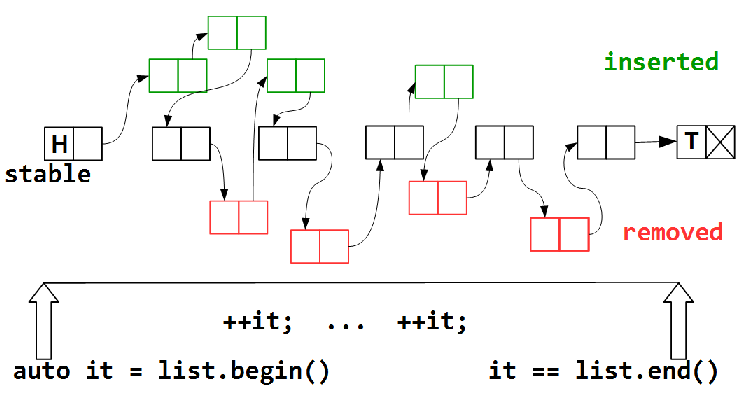
反復-コンテナの要素を反復処理-時間がかかり、その間にコンテナからいくつかの要素が削除され、他の要素が追加されますが、トラバースの全時間にわたってコンテナに存在する安定した（空の可能性のある）要素のサブセットが存在する必要がありますlist.begin()



からlist.end()



。 それらに加えて、追加された要素のいくつかと、削除された要素のいくつかを、カードが置かれるときに訪問できます。 明らかに、ロックフリーマップ内のすべての要素を訪問するタスクは不可能です。ラウンドの全時間にわたってコンテナの状態を凍結することはできません。 このような凍結とは、実際には、他のスレッドがコンテナに対して変更操作を実行することを禁止することを意味します。これは、ブロッキングと同等です。



物議を醸す声明
実際、競合するコンテナの状態を「フリーズ」する技術がありますが、これは他のスレッドがコンテナを変更するのを防ぎません-その要素を追加/削除します。 おそらく、これらのテクニックの中で最も有名なのはバージョン付きツリーです。 一番下の行は、コンテナの複数のバージョンが1つのツリーに格納されることです。 そのようなツリーに追加するたびに、別のバージョンが生成されます。それは、不変のノードを他のバージョン（ツリー）と共有する独自のルートを持つツリーです。 バージョン管理されたツリーのコンシューマーは、ツリーの最新バージョン（最新のルート）を取得し、ツリーで動作する間、このバージョンはツリーに残ります。 バージョンに関連付けられているコンシューマストリームがなくなるとすぐに、バージョン（つまり、このバージョンに属するすべてのノード）を安全に削除できます。

別の手法は、スナップショットをサポートする競合コンテナーです（コンテナースナップショット）。 ある意味では、バージョン管理されたコンテナに似ています。



これらの手法は両方とも、バージョンまたはスナップショットを保存するためのメモリ消費量の増加、および内部構造をサポートするための追加の操作を伴います。 多くの場合、このような技術が提供する利点と比較して、この過剰な支出は無視できます。

この記事では、同様の手法を使用せずに競合する連想コンテナを検討します。 つまり、問題はこれです。まさにその内部構造により、要素の安全なバイパスを可能にするような競争力のあるコンテナを構築することは可能でしょうか？



したがって、安定したサブセットからのすべてのノードへの保証された訪問は、競合するコンテナのバイパスであると考えます。



「競合するコンテナのバイパスと見なされるもの」という質問に加えて、2つの問題があります。



問題1 。 イテレータは、本質的にコンテナ要素への特殊なポインタです。 イテレータを使用して、要素自体にアクセスします。 ただし、競合するコンテナでは、イテレータが配置されている要素はいつでも削除できます。 つまり、イテレータはいつでも無効になる可能性があります-削除された要素、つまりゴミを指します：







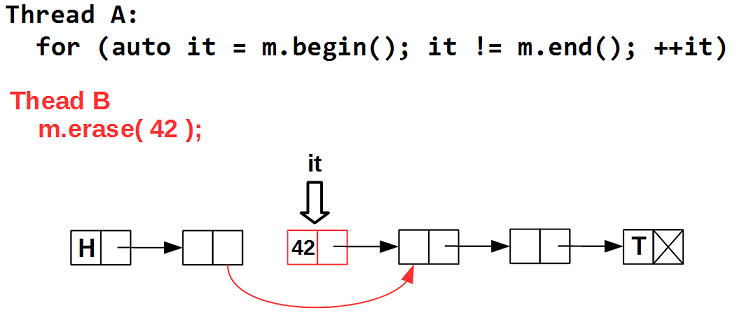
ハザードポインター回路におけるこの問題の解決策は、実際にはハザードポインターです。 HPスキームでは、ポインターが危険であると宣言されている間、ポインター（ポインター）を物理的に削除できない、つまり、ガベージカボチャにならないことを思い出してください。 以下の便利な抽象化、 guarded_ptr



保護ポインターを導入します。 



 template <typename T> struct guarded_ptr { hp_guard hp; //   T * ptr; //   guarded_ptr(std::atomic<T *>& p) { ptr = hp.protect( p ); } ~guarded_ptr() { hp.clear(); } T * operator ->() const { return ptr; } explicit operator bool() const { return ptr != nullptr; } };


ご覧のとおり、 guarded_ptr



はハザードポインターを備えた単なるポインターです。 ハザードポインターhp



は、 ptr



要素へのポインターを保護し、物理的に削除されないようにします。 ストリームBがイテレータが配置されている要素を削除しても、この要素はコンテナから除外されますが、イテレータのハザードポインタにこの要素へのリンクが含まれるまで物理的に削除されません。



したがって、HPスキーマでは、反復子クラスは次のようになります。 



 template <typename T> class iterator { guarded_ptr<T> gp; public: T* operator ->() { return gp.ptr; } T& operator *() { return *gp.ptr; } iterator& operator++(); };


エポックベース
（ ユーザー空間RCUがguarded_ptr



エポックベースのスキームでは、 guarded_ptr



は必要ありません。1つの時代に反復（コンテナのすべての要素のトラバーサル）を実行する必要があります。 



 urcu.lock(); //    for ( auto it = m.begin(); it != m.end(); ++it ) { // ... } urcu.unlock(); //




問題2 ：次の項目に進みます。







特定のスレッドBが、イテレータが配置されている要素（この場合は42）に続く要素を削除すると、イテレータをインクリメントする操作は、削除された要素の呼び出し、つまりガベージになります。



この問題は、スレッドがコンテナをバイパスしていることを知らず、要素を自由に削除/追加できるため、最初の問題よりも複雑です。 イテレータが指す要素を何らかの方法でマークし、要素を削除するときにそのようなフラグを分析することを考えることができますが、これは少なくともコンテナの内部構造を複雑にします（そして、最大で、そのような推論は何にもつながりません）。 興味深いデータ構造からわかる別の方法があります-マルチレベル配列。



マルチレベル配列



このデータ構造は、2013年にSteve Feldmanによって提案された連想コンテナ、つまりハッシュマップです。







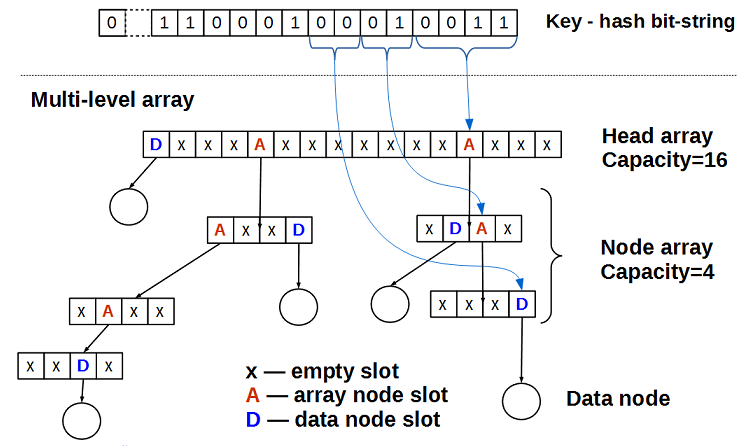
ハッシュが一定の長さのビット文字列であると想像してください。 この文字列のビットをマルチレベル配列のインデックスと見なします：最初のMビットは、ヘッド配列のヘッド配列のインデックスです（図ではM = 4、つまり、ヘッド配列のサイズは2 ** 4 = 16です）、Nビットの次の部分は基礎となるノード配列のインデックス（図では、N = 2で、ノード配列の次元は2 ** 2 = 4です）。 配列要素には次のものがあります。





空のマルチレベル配列は、すべてのセルが空のヘッド配列のみで構成されます。



次のアルゴリズムに従って、マルチレベル配列のキーキーを使用してデータdata



を追加します。





ご覧のように、挿入アルゴリズムは非常にシンプルで直感的です-言葉で説明するよりも描く方が簡単です。 削除アルゴリズムはさらに簡単です：削除されたキーのハッシュ値をビット文字列として考慮し、ビットを選択して配列内のインデックスとして解釈し、セルが空またはデータを含む配列へのリンクを下ります。 セルが空の場合、キー（より正確には、そのハッシュ）がコンテナー内になく、削除するものがないことを意味します。 セルにデータが含まれ、このデータのキーが目的のキーである場合、アトミックCAS操作を使用してセル値をnullptr



変更します。 削除するとき、配列のセルをゼロにするだけで、node_array自体は決して削除されないことに注意してください-この事実は将来役に立つでしょう。



質問は未解決のままです。配列セルに含まれる内容を区別する方法-次のレベルの配列へのデータまたはポインター。 通常のプログラミングでは、配列の各スロットにブールタグを配置します。 



 struct array_slot { union { T* data; node_array* array; }; bool is_array; // ,    — data  array };


しかし、私たちのプログラミングは異常であり、このアプローチは私たちには適していないでしょう。 異常なことは、データの長さに制限があるアトミックプリミティブCASを操作する必要があることです。 つまり、1つのCASでセルの値とis_array



属性をアトミックに変更できる必要があります。

ロックフリーエピックの前の部分を読んで、 マークされたポインターのようなものがあることを知っていれば、これは問題ではありません。 is_array



を配列セルポインターのis_array



ビットに保存します。 



 template <typename T> using array_slot = marked_ptr<T*, 3 >;


したがって、配列セルは単なるポインターであり、内部フラグには最後の2ビット（ marked_ptr



マスク3）を使用します。「セルには次のレベルの配列へのポインターが含まれます」記号に1ビット、... ？..



挿入アルゴリズムをよく見てください。 ステップ3bおよび4bは、セルの分割、つまり、データを含むセルから基礎となる配列へのポインターを含むセルへの変換について説明しています。 そのような変換は、以下を必要とするため、非常に時間がかかります。





これらのすべてのアクションが実行されている間、分裂可能なセルは未定義の状態にあります。 2番目の最下位ビットでエンコードするのはこの状態です。 「セルが分割されています」というフラグを満たしたマルチレベルアレイ上のすべての操作は、このフラグでアクティブスピンを使用して、そのようなセルの分割が完了するのを待っています。





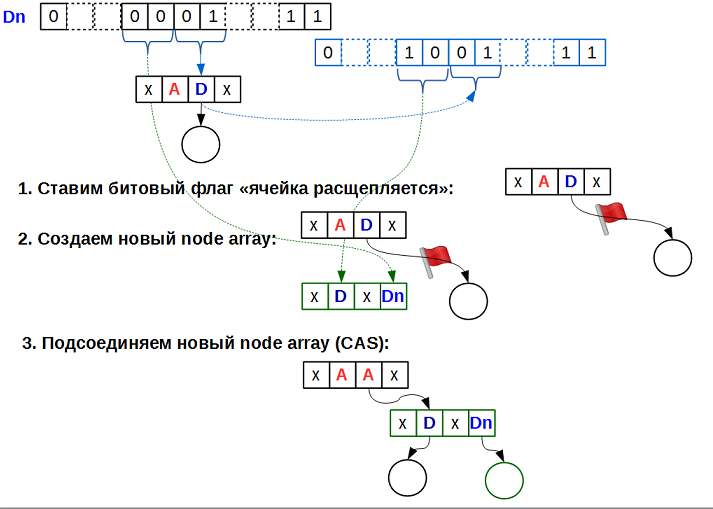
図では、黒のデータが追加されたキーDn



、青が既存のD







限界ノート-ロックフリーコンテナの量子力学
分割セルについてこれをすべて書いていたときに、考えが浮上しました：このフラグは必要です、なぜならそれは検索操作を含む他のすべてのフローの回転につながるので、set / mapのようなコンテナにとって最速でなければなりませんか？ 。



操作を検討してください。 一般に、mapは、キーの検索、挿入、および削除の3つの操作のみをサポートします（残りの操作はさまざまです）。 検索では、「セルが分割段階にある」という事実は絶対に重要ではありません。検索では、セルの種類を調べる必要があります。 セルにデータへのポインターが含まれている場合、データキーを探しているものと比較する必要があります（データでセルに遭遇したため、ビット文字列のプレフィックス（キーとセル内のデータのハッシュ）は同じであり、セル内のデータを検索できることを意味します） セルが配列へのポインターである場合は、この配列に移動して検索を続ける必要があります。 探しているキーがセルが分割されているデータそのものであると仮定します。つまり、あるスレッドがキーKを探し、別のスレッドが同じキーKのデータを追加し、これが同時に発生する状況があるとします。 これは同時に発生するため、検索操作は「キーが見つかった」場合と「キーが見つからなかった」場合の両方で正しいものになります。 検索操作に分割フラグは必要ないことがわかります。



挿入操作。 挿入が分割セルでつまずくと、別のストリームが、現在のストリームと同じキーハッシュ値のプレフィックスを持つデータを追加します。 この場合、両方のストリーム（両方の挿入操作）は、各node_arrayを作成し、それを分割セルの値として設定しようとすることにより、互いに助け合います。 セル値はCASプリミティブによって設定され、node_arrayは決して削除されないため（つまり、node_arrayへのポインターにABAの問題はない）、挿入スレッドの1つだけが勝者となり（分割セルの新しい値を設定）、2番目のスレッドはセル値を検出します変更されたため、彼（この2番目のスレッド）が作成しようとしているnode_arrayを削除し、表示された分割セルの値を使用する必要があります。 つまり、分割フラグも挿入する必要がありません。



取り外し。 削除する前に、削除する必要があるものを見つける必要があります。つまり、この意味での削除は検索と同等であり、分割フラグは必要ありません。



考慮する必要がある唯一の操作は、データの更新、更新です。



セル分割フラグが低優先度のスレッドを設定してから強制終了される場合、他の優先度のスレッドは分割が完了するまで待機するため、つまり低優先度のスレッドが動作するまで待機するため、これはコンテナの全体的なパフォーマンスにとって非常に痛いことがあります。 この場合、分割フラグを削除すると非常に便利です。



マルチレベル配列のデータ構造はシンプルで興味深いものですが、その機能（「欠陥」を書きたかったのですが、それでも機能です）は次のとおりです。





ただし、キーのサイズが一定の場合（または理想的なハッシュ関数がある場合）、マルチレベル配列は非常に優れたロックフリーコンテナーであるIMHOです。



原則として、マルチレベル配列を一般化して衝突リストをサポートすることができます。このため、データの代わりにロックのないリストを衝突のリストとして使用するだけで十分です。 可変長キーの別の一般化：短いキーには、ビット文字列内の他のすべてのビットがゼロに等しいと仮定します。



さらなるファンタジー
「キー」という単語を「インデックス」という単語に置き換えることも興味深いです。この場合、ロックフリーのベクトルに非常によく似たものが得られます。 配列の現在のサイズを個別のアトミック変数に格納することにより、 push_back



およびpop_back



操作を実行できます。 ただし、2つのストリームが同時にpush_back



実行する場合にのみ、しばらくの間ホールが発生push_back



状況が発生します。ストリームAはカウンターをインクリメントし、インデックスj



を取得して強制終了し、ストリームBはインデックスj+1



を取得してこのインデックスに正常に挿入します。 ここでは、2（またはM）個の未接続メモリセルでCASをアトミックに実行できる2-CAS動作（またはその一般化、マルチCAS、MCAS）が役立ちます。



ただし、この記事の目的上、マルチレベル配列の1つのプロパティが重要です。一度作成されたノード配列は削除されません。 そしてこれから強力な結果が得られます。 マルチレベル配列はスレッドセーフなイテレータをサポートし 、さらに、これらは双方向イテレータです。 実際、ノード配列は削除されないため、イテレーターはノード配列へのポインターに加えて、セルへの「ポインター」であるノード配列内のインデックスです。 



 class iterator { guarded_ptr<T> gp_; node_array* node_; int node_index_; };


競合スレッドはイテレータが配置されているデータを削除できるため、ここでguarded_ptr



が必要です。 guarded_ptr



、物理的な削除を防ぎます。 イテレータは、コンテナから削除された要素を指すことができることが判明しました。これは、ロックフリーデータ構造のもう1つの予期しないプロパティです。 しかし、慎重に考えると、このプロパティは理解できます。競争の激しいコンテナである絶えず変化する世界では、保証できるのは1つだけです。イテレータを配置する時点で、このセルには有効なデータが含まれていました。

node_



へのnode_



ポインターとその中のインデックスnode_index_



、コンテナーの次（または前）の要素に移動するためにイテレーターで必要です。つまり、コンテナー内のイテレーターの現在の位置を実際に決定します。



ハッシュ値ではなく一定サイズのキーがある場合、マルチレベルの配列バイパスが順序付けられることに注意するのは興味深いことです。



商業休憩
実装の詳細に興味がある場合は、FeldmanHashSet / Mapクラスのlibcdsで確認できます（ここでの主な操作は、HPベースのSMRの場合はcds/intrusive/impl/feldman_hashset.h



cds/intrusive/feldman_hashset_rcu.h



、ユーザースペースRCUの場合はcds/intrusive/feldman_hashset_rcu.h



です） 。



要約すると、スレッドセーフなイテレータをサポートする競合するコンテナがまだあり、これらのコンテナの1つはマルチレベル配列です。 他にありますか？..多くの興味深いロックフリーマップの基礎となる反復可能なロックフリーリストを作成することは可能ですか？..



この質問に対する答えは次の記事にあります。



ロックフリーのデータ構造
開始する

基本：



中：



外から：





More articles:


All Articles