制限/導関数/積分を見つけるための簡単なタスクの独自のジェネレーターの作成方法については、katの後に説明します。
Ps同様のプログラムを作成した経験については、前のパートで説明しています。
写真からわかるように、タスクはLaTexを使用してPDFで生成されます。 彼についてはすでにさまざまな記事がありましたので、紹介部分は省略します。 Pascalを使用してタスクを実装および作成します(ただし、一般的なアルゴリズムを説明および非表示にし、スポイラーのすべてのコードを非表示にします)。
さあ始めましょう
三角関数は多項式に正確に基づいているため、まず多項式(多項式)の概念を定義する必要があります。 標準操作の一部として、次を入力する必要があります。
- 多項式加算
- 多項式の減算
- 多項式の乗算
- 卒業
- テキスト翻訳
- デリバティブ
- インテグラル
多項式クラス
型多項式=レコード
st:integer; //多項式の次数
kof:実数の配列; // x ^ iの係数
function into(x:real):実数;
クラス関数演算子+(a、b:多項式):多項式;
var i、stn:整数;
rez:多項式;
始める
if(a.st> b.st)then stn:= a.st
そうでなければstn:= b.st;
setlength(rez.kof、stn + 1);
for i:= 0からstn do
rez.kof [i]:= 0;
for i:= 0からstn do
始める
if(i <= a.st)then
rez.kof [i]:= rez.kof [i] + a.kof [i];
if(i <= b.st)then
rez.kof [i]:= rez.kof [i] + b.kof [i];
終わり;
rez.st:=stn;
結果:= rez;
終わり;
クラス関数演算子-(a、b:多項式):多項式;
var i、stn:整数;
rez:多項式;
始める
if(a.st> b.st)then stn:= a.st
そうでなければstn:= b.st;
setlength(rez.kof、stn + 1);
for i:= 0からstn do
rez.kof [i]:= 0;
for i:= 0からstn do
始める
if(i <= a.st)then
rez.kof [i]:= rez.kof [i] + a.kof [i];
if(i <= b.st)then
rez.kof [i]:= rez.kof [i] -b.kof [i];
終わり;
while(rez.kof [stn] = 0)do
始める
setlength(rez.kof、stn);
stn:= stn-1;
終わり;
rez.st:=stn;
結果:= rez;
終わり;
クラス関数演算子*(a、b:多項式):多項式;
var i、j、stn:整数;
rez:多項式;
始める
stn:= a.st + b.st;
setlength(rez.kof、stn + 1);
for i:= 0からstn do
rez.kof [i]:= 0;
for i:= 0 to a.st do
for j:= 0 to b.st do
始める
rez.kof [i + j]:= rez.kof [i + j] + a.kof [i] * b.kof [j];
終わり;
while(rez.kof [stn] = 0)do
始める
setlength(rez.kof、stn);
stn:= stn-1;
終わり;
rez.st:=stn;
結果:= rez;
終わり;
クラス関数演算子*(a:整数; b:多項式):多項式;
var i:整数;
始める
for i:= 0 to b.st do
b.kof [i]:= a * b.kof [i];
結果:= b;
終わり;
クラス関数演算子(a:多項式; n:整数):多項式;
var i:整数;
rez:多項式;
始める
rez.st:=0;
setlength(rez.kof、1);
rez.kof [0]:= 1;
for i:= 1からn
rez:= rez * a;
結果:= rez;
終わり;
プロシージャnw(x:整数);
function pltostr:string; //文字列変数へ
手続き導関数; //導関数
手続き積分; //積分
終わり;
手続き多項式.nw(x:整数);
var
i:整数;
始める
st:= x;
setlength(kof、st + 1);
for i:= 0からst do
kof [i]:=ランダム(-10,10);
while(kof [st] = 0)do
kof [st]:=ランダム(-10,10);
終わり;
プロシージャpolynomial.integral;
var
i:整数;
始める
setlength(kof、st + 2);
for i:= st downto 1 do
kof [i + 1]:= kof [i] / i;
kof [0]:= 0;
st:= st + 1;
setlength(kof、st + 1);
終わり;
プロシージャpolynomial.derivative;
var
i:整数;
始める
for i:= 1からst do
kof [i-1]:= kof [i] * i;
st:= st-1;
setlength(kof、st + 1);
終わり;
st:integer; //多項式の次数
kof:実数の配列; // x ^ iの係数
function into(x:real):実数;
クラス関数演算子+(a、b:多項式):多項式;
var i、stn:整数;
rez:多項式;
始める
if(a.st> b.st)then stn:= a.st
そうでなければstn:= b.st;
setlength(rez.kof、stn + 1);
for i:= 0からstn do
rez.kof [i]:= 0;
for i:= 0からstn do
始める
if(i <= a.st)then
rez.kof [i]:= rez.kof [i] + a.kof [i];
if(i <= b.st)then
rez.kof [i]:= rez.kof [i] + b.kof [i];
終わり;
rez.st:=stn;
結果:= rez;
終わり;
クラス関数演算子-(a、b:多項式):多項式;
var i、stn:整数;
rez:多項式;
始める
if(a.st> b.st)then stn:= a.st
そうでなければstn:= b.st;
setlength(rez.kof、stn + 1);
for i:= 0からstn do
rez.kof [i]:= 0;
for i:= 0からstn do
始める
if(i <= a.st)then
rez.kof [i]:= rez.kof [i] + a.kof [i];
if(i <= b.st)then
rez.kof [i]:= rez.kof [i] -b.kof [i];
終わり;
while(rez.kof [stn] = 0)do
始める
setlength(rez.kof、stn);
stn:= stn-1;
終わり;
rez.st:=stn;
結果:= rez;
終わり;
クラス関数演算子*(a、b:多項式):多項式;
var i、j、stn:整数;
rez:多項式;
始める
stn:= a.st + b.st;
setlength(rez.kof、stn + 1);
for i:= 0からstn do
rez.kof [i]:= 0;
for i:= 0 to a.st do
for j:= 0 to b.st do
始める
rez.kof [i + j]:= rez.kof [i + j] + a.kof [i] * b.kof [j];
終わり;
while(rez.kof [stn] = 0)do
始める
setlength(rez.kof、stn);
stn:= stn-1;
終わり;
rez.st:=stn;
結果:= rez;
終わり;
クラス関数演算子*(a:整数; b:多項式):多項式;
var i:整数;
始める
for i:= 0 to b.st do
b.kof [i]:= a * b.kof [i];
結果:= b;
終わり;
クラス関数演算子(a:多項式; n:整数):多項式;
var i:整数;
rez:多項式;
始める
rez.st:=0;
setlength(rez.kof、1);
rez.kof [0]:= 1;
for i:= 1からn
rez:= rez * a;
結果:= rez;
終わり;
プロシージャnw(x:整数);
function pltostr:string; //文字列変数へ
手続き導関数; //導関数
手続き積分; //積分
終わり;
手続き多項式.nw(x:整数);
var
i:整数;
始める
st:= x;
setlength(kof、st + 1);
for i:= 0からst do
kof [i]:=ランダム(-10,10);
while(kof [st] = 0)do
kof [st]:=ランダム(-10,10);
終わり;
プロシージャpolynomial.integral;
var
i:整数;
始める
setlength(kof、st + 2);
for i:= st downto 1 do
kof [i + 1]:= kof [i] / i;
kof [0]:= 0;
st:= st + 1;
setlength(kof、st + 1);
終わり;
プロシージャpolynomial.derivative;
var
i:整数;
始める
for i:= 1からst do
kof [i-1]:= kof [i] * i;
st:= st-1;
setlength(kof、st + 1);
終わり;
通常の多項式に従って、ルートを持つ多項式を導入する必要があります(そのため、ルートを検索したり、分数を減らしたりできます)。
ただし、同じクラスに対してだけでなく、通常の多項式に対しても同じプロパティを作成する必要があるため、特殊性があります。
根を持つ多項式
タイプpolynomialwithroot = record
st:integer; //多項式の次数
root:整数の配列; //多項式の根
kof:整数の配列; // x ^ iの係数
クラス関数演算子+(a、b:多項式withroot):多項式;
var i、stn:整数;
rez:多項式;
始める
if(a.st> b.st)then stn:= a.st
そうでなければstn:= b.st;
setlength(rez.kof、stn + 1);
for i:= 0からstn do
rez.kof [i]:= 0;
for i:= 0からstn do
始める
if(i <= a.st)then
rez.kof [i]:= rez.kof [i] + a.kof [i];
if(i <= b.st)then
rez.kof [i]:= rez.kof [i] + b.kof [i];
終わり;
rez.st:=stn;
結果:= rez;
終わり;
クラス関数演算子+(a:Polynomialwithroot; b:多項式):多項式;
var i、stn:整数;
rez:多項式;
始める
if(a.st> b.st)then stn:= a.st
そうでなければstn:= b.st;
setlength(rez.kof、stn + 1);
for i:= 0からstn do
rez.kof [i]:= 0;
for i:= 0からstn do
始める
if(i <= a.st)then
rez.kof [i]:= rez.kof [i] + a.kof [i];
if(i <= b.st)then
rez.kof [i]:= rez.kof [i] + b.kof [i];
終わり;
rez.st:=stn;
結果:= rez;
終わり;
クラス関数演算子+(b:多項式; a:多項式とルート):多項式;
// var i:整数;
// rez:多項式;
始める
結果:= a + b;
終わり;
クラス関数演算子-(a、b:多項式withroot):多項式;
var i、stn:整数;
rez:多項式;
始める
if(a.st> b.st)then stn:= a.st
そうでなければstn:= b.st;
setlength(rez.kof、stn + 1);
for i:= 0からstn do
rez.kof [i]:= 0;
for i:= 0からstn do
始める
if(i <= a.st)then
rez.kof [i]:= rez.kof [i] + a.kof [i];
if(i <= b.st)then
rez.kof [i]:= rez.kof [i] -b.kof [i];
終わり;
while(rez.kof [stn] = 0)do
始める
setlength(rez.kof、stn);
stn:= stn-1;
終わり;
rez.st:=stn;
結果:= rez;
終わり;
クラス関数演算子-(a:多項式とルート; b:多項式):多項式;
var i、stn:整数;
rez:多項式;
始める
if(a.st> b.st)then stn:= a.st
そうでなければstn:= b.st;
setlength(rez.kof、stn + 1);
for i:= 0からstn do
rez.kof [i]:= 0;
for i:= 0からstn do
始める
if(i <= a.st)then
rez.kof [i]:= rez.kof [i] + a.kof [i];
if(i <= b.st)then
rez.kof [i]:= rez.kof [i] -b.kof [i];
終わり;
while(rez.kof [stn] = 0)do
始める
setlength(rez.kof、stn);
stn:= stn-1;
終わり;
rez.st:=stn;
結果:= rez;
終わり;
クラス関数演算子-(b:多項式; a:多項式付きのルート):多項式;
var i、stn:整数;
rez:多項式;
始める
if(a.st> b.st)then stn:= a.st
そうでなければstn:= b.st;
setlength(rez.kof、stn + 1);
for i:= 0からstn do
rez.kof [i]:= 0;
for i:= 0からstn do
始める
if(i <= a.st)then
rez.kof [i]:= rez.kof [i] + a.kof [i];
if(i <= b.st)then
rez.kof [i]:= rez.kof [i] -b.kof [i];
終わり;
while(rez.kof [stn] = 0)do
始める
setlength(rez.kof、stn);
stn:= stn-1;
終わり;
rez.st:=stn;
結果:= rez;
終わり;
クラス関数演算子*(a、b:多項式withroot):多項式withroot;
var i、j、stn:整数;
rez:多項式のルート。
始める
stn:= a.st + b.st;
setlength(rez.kof、stn + 1);
for i:= 0からstn do
rez.kof [i]:= 0;
for i:= 0 to a.st do
for j:= 0 to b.st do
始める
rez.kof [i + j]:= rez.kof [i + j] + a.kof [i] * b.kof [j];
終わり;
while(rez.kof [stn] = 0)do
始める
setlength(rez.kof、stn);
stn:= stn-1;
終わり;
rez.st:=stn;
setlength(rez.root、rez.st);
for i:= 0 to a.st-1 do
rez.root [i]:= a.root [i];
for i:= 0 to b.st-1 do
rez.root [a.st + i]:= b.root [i];
結果:= rez;
終わり;
クラス関数演算子*(a:多項式とルート; b:多項式):多項式;
var i、j、stn:整数;
rez:多項式;
始める
stn:= a.st + b.st;
setlength(rez.kof、stn + 1);
for i:= 0からstn do
rez.kof [i]:= 0;
for i:= 0 to a.st do
for j:= 0 to b.st do
始める
rez.kof [i + j]:= rez.kof [i + j] + a.kof [i] * b.kof [j];
終わり;
while(rez.kof [stn] = 0)do
始める
setlength(rez.kof、stn);
stn:= stn-1;
終わり;
rez.st:=stn;
結果:= rez;
終わり;
クラス関数演算子*(b:多項式; a:多項式とルート):多項式;
// var i、j、stn:integer;
// rez:多項式;
始める
結果:= a * b;
終わり;
クラス関数演算子(a:多項式withroot; n:整数):多項式withroot;
var i:整数;
rez:多項式のルート。
始める
rez:= a;
for i:= 2からn
rez:= rez * a;
結果:= rez;
終わり;
プロシージャnw;
プロシージャルート(x:整数);
関数pltostr:文字列。
終わり;
プロシージャ多項式withroot.roots(x:整数);
var i:整数;
始める
st:= x;
setlength(root、st);
for i:= 0からst-1まで
始める
ルート[i]:=ランダム(-5,5);
終わり;
nw;
終わり;
プロシージャ多項式withroot.nw;
var
i、j、合計:整数;
tk:整数の配列。
dop:整数;
始める
setlength(kof、st + 1);
setlength(tk、st + 1);
for i:= 0からst-1まで
kof [i]:= 0;
for i:= 0からst-1まで
始める
j:= 0からst do
tk [j]:= 0;
while(tk [st] = 0)do
始める
sum:= 0;
j:= 0からst-1まで
sum:= sum + tk [j];
if(sum =(i + 1))then
始める
dop:= 1;
j:= 0からst-1まで
if(tk [j] = 1)then
dop:= dop * root [j];
for j:= 0 to i do
dop:=-dop;
kof [st-i-1]:= kof [st-i-1] + dop;
終わり;
tk [0]:= tk [0] +1;
j:= 0からst-1まで
始める
tk [j + 1]:= tk [j + 1] +(tk [j] div 2);
tk [j]:= tk [j] mod 2;
終わり;
終わり;
終わり;
kof [st]:= 1;
終わり;
st:integer; //多項式の次数
root:整数の配列; //多項式の根
kof:整数の配列; // x ^ iの係数
クラス関数演算子+(a、b:多項式withroot):多項式;
var i、stn:整数;
rez:多項式;
始める
if(a.st> b.st)then stn:= a.st
そうでなければstn:= b.st;
setlength(rez.kof、stn + 1);
for i:= 0からstn do
rez.kof [i]:= 0;
for i:= 0からstn do
始める
if(i <= a.st)then
rez.kof [i]:= rez.kof [i] + a.kof [i];
if(i <= b.st)then
rez.kof [i]:= rez.kof [i] + b.kof [i];
終わり;
rez.st:=stn;
結果:= rez;
終わり;
クラス関数演算子+(a:Polynomialwithroot; b:多項式):多項式;
var i、stn:整数;
rez:多項式;
始める
if(a.st> b.st)then stn:= a.st
そうでなければstn:= b.st;
setlength(rez.kof、stn + 1);
for i:= 0からstn do
rez.kof [i]:= 0;
for i:= 0からstn do
始める
if(i <= a.st)then
rez.kof [i]:= rez.kof [i] + a.kof [i];
if(i <= b.st)then
rez.kof [i]:= rez.kof [i] + b.kof [i];
終わり;
rez.st:=stn;
結果:= rez;
終わり;
クラス関数演算子+(b:多項式; a:多項式とルート):多項式;
// var i:整数;
// rez:多項式;
始める
結果:= a + b;
終わり;
クラス関数演算子-(a、b:多項式withroot):多項式;
var i、stn:整数;
rez:多項式;
始める
if(a.st> b.st)then stn:= a.st
そうでなければstn:= b.st;
setlength(rez.kof、stn + 1);
for i:= 0からstn do
rez.kof [i]:= 0;
for i:= 0からstn do
始める
if(i <= a.st)then
rez.kof [i]:= rez.kof [i] + a.kof [i];
if(i <= b.st)then
rez.kof [i]:= rez.kof [i] -b.kof [i];
終わり;
while(rez.kof [stn] = 0)do
始める
setlength(rez.kof、stn);
stn:= stn-1;
終わり;
rez.st:=stn;
結果:= rez;
終わり;
クラス関数演算子-(a:多項式とルート; b:多項式):多項式;
var i、stn:整数;
rez:多項式;
始める
if(a.st> b.st)then stn:= a.st
そうでなければstn:= b.st;
setlength(rez.kof、stn + 1);
for i:= 0からstn do
rez.kof [i]:= 0;
for i:= 0からstn do
始める
if(i <= a.st)then
rez.kof [i]:= rez.kof [i] + a.kof [i];
if(i <= b.st)then
rez.kof [i]:= rez.kof [i] -b.kof [i];
終わり;
while(rez.kof [stn] = 0)do
始める
setlength(rez.kof、stn);
stn:= stn-1;
終わり;
rez.st:=stn;
結果:= rez;
終わり;
クラス関数演算子-(b:多項式; a:多項式付きのルート):多項式;
var i、stn:整数;
rez:多項式;
始める
if(a.st> b.st)then stn:= a.st
そうでなければstn:= b.st;
setlength(rez.kof、stn + 1);
for i:= 0からstn do
rez.kof [i]:= 0;
for i:= 0からstn do
始める
if(i <= a.st)then
rez.kof [i]:= rez.kof [i] + a.kof [i];
if(i <= b.st)then
rez.kof [i]:= rez.kof [i] -b.kof [i];
終わり;
while(rez.kof [stn] = 0)do
始める
setlength(rez.kof、stn);
stn:= stn-1;
終わり;
rez.st:=stn;
結果:= rez;
終わり;
クラス関数演算子*(a、b:多項式withroot):多項式withroot;
var i、j、stn:整数;
rez:多項式のルート。
始める
stn:= a.st + b.st;
setlength(rez.kof、stn + 1);
for i:= 0からstn do
rez.kof [i]:= 0;
for i:= 0 to a.st do
for j:= 0 to b.st do
始める
rez.kof [i + j]:= rez.kof [i + j] + a.kof [i] * b.kof [j];
終わり;
while(rez.kof [stn] = 0)do
始める
setlength(rez.kof、stn);
stn:= stn-1;
終わり;
rez.st:=stn;
setlength(rez.root、rez.st);
for i:= 0 to a.st-1 do
rez.root [i]:= a.root [i];
for i:= 0 to b.st-1 do
rez.root [a.st + i]:= b.root [i];
結果:= rez;
終わり;
クラス関数演算子*(a:多項式とルート; b:多項式):多項式;
var i、j、stn:整数;
rez:多項式;
始める
stn:= a.st + b.st;
setlength(rez.kof、stn + 1);
for i:= 0からstn do
rez.kof [i]:= 0;
for i:= 0 to a.st do
for j:= 0 to b.st do
始める
rez.kof [i + j]:= rez.kof [i + j] + a.kof [i] * b.kof [j];
終わり;
while(rez.kof [stn] = 0)do
始める
setlength(rez.kof、stn);
stn:= stn-1;
終わり;
rez.st:=stn;
結果:= rez;
終わり;
クラス関数演算子*(b:多項式; a:多項式とルート):多項式;
// var i、j、stn:integer;
// rez:多項式;
始める
結果:= a * b;
終わり;
クラス関数演算子(a:多項式withroot; n:整数):多項式withroot;
var i:整数;
rez:多項式のルート。
始める
rez:= a;
for i:= 2からn
rez:= rez * a;
結果:= rez;
終わり;
プロシージャnw;
プロシージャルート(x:整数);
関数pltostr:文字列。
終わり;
プロシージャ多項式withroot.roots(x:整数);
var i:整数;
始める
st:= x;
setlength(root、st);
for i:= 0からst-1まで
始める
ルート[i]:=ランダム(-5,5);
終わり;
nw;
終わり;
プロシージャ多項式withroot.nw;
var
i、j、合計:整数;
tk:整数の配列。
dop:整数;
始める
setlength(kof、st + 1);
setlength(tk、st + 1);
for i:= 0からst-1まで
kof [i]:= 0;
for i:= 0からst-1まで
始める
j:= 0からst do
tk [j]:= 0;
while(tk [st] = 0)do
始める
sum:= 0;
j:= 0からst-1まで
sum:= sum + tk [j];
if(sum =(i + 1))then
始める
dop:= 1;
j:= 0からst-1まで
if(tk [j] = 1)then
dop:= dop * root [j];
for j:= 0 to i do
dop:=-dop;
kof [st-i-1]:= kof [st-i-1] + dop;
終わり;
tk [0]:= tk [0] +1;
j:= 0からst-1まで
始める
tk [j + 1]:= tk [j + 1] +(tk [j] div 2);
tk [j]:= tk [j] mod 2;
終わり;
終わり;
終わり;
kof [st]:= 1;
終わり;
次に、同様の例に従って、三角関数(対数とe ^ xを含む)を使用します。
三角関数
タイプsinx =レコード
x:多項式;
s:文字列;
プロシージャnw;
手続き導関数; //導関数
終わり;
タイプcosx =レコード
x:多項式;
s:文字列;
プロシージャnw;
手続き導関数; //導関数
終わり;
タイプtgx =レコード
x:多項式;
s:文字列;
プロシージャnw;
手続き導関数; //導関数
終わり;
タイプctgx =レコード
x:多項式;
s:文字列;
プロシージャnw;
手続き導関数; //導関数
終わり;
タイプlnx =レコード
s:文字列;
x:多項式;
プロシージャnw;
手続き派生物;
終わり;
タイプex =レコード
s:文字列;
f、x:多項式;
プロシージャnw;
手続き派生物;
終わり;
x:多項式;
s:文字列;
プロシージャnw;
手続き導関数; //導関数
終わり;
タイプcosx =レコード
x:多項式;
s:文字列;
プロシージャnw;
手続き導関数; //導関数
終わり;
タイプtgx =レコード
x:多項式;
s:文字列;
プロシージャnw;
手続き導関数; //導関数
終わり;
タイプctgx =レコード
x:多項式;
s:文字列;
プロシージャnw;
手続き導関数; //導関数
終わり;
タイプlnx =レコード
s:文字列;
x:多項式;
プロシージャnw;
手続き派生物;
終わり;
タイプex =レコード
s:文字列;
f、x:多項式;
プロシージャnw;
手続き派生物;
終わり;
事前に三角関数式を使用しないように予約します。 これにより、解くだけでなく、マッピングタスクも複雑になります。
TeXについて少し
TeXでの作業を簡素化するために、別のクラスが作成されたため、後ですべてを別のモジュールに入れることができます。
クラスは以下を担当します。
- 新しいtexファイルの作成(作成および導入ブロック)
- 行ごとにテキストを追加します(行の最後に新しい行への遷移があります)
- 新しいtexファイルを作成します
- Texファイルを閉じる(ブロックを閉じてファイルを停止する)
- コンピューターにインストールされたTexを介してPDFを作成する
- PDFファイルを開く
モジュールコード
タイプtex =レコード
namefl:文字列;
プロシージャnewtex(s:文字列);
プロシージャの追加(s:文字列);
プロシージャclosetex;
プロシージャcreatepdf;
手順openpdf;
終わり;
実装
プロシージャtex.newtex(s:文字列);
var
t:テキスト;
始める
namefl:= s;
assign(t、s + '。tex');
書き換え(t);
writeln(t、 '\ documentclass [12pt] {article}');
writeln(t、 '\ usepackage {amsmath}');
writeln(t、 '%\ usepackage [rus] {babel}');
writeln(t、 '%\ usepackage [cp1251] {inputenc}');
writeln(t、 '\ begin {document}');
閉じる(t);
終わり;
プロシージャtex.add(s:文字列);
var
t:テキスト;
始める
assign(t、namefl + '。tex');
追加(t);
writeln(t、 '\ [');
writeln(t、s);
writeln(t、 '\]');
閉じる(t);
終わり;
プロシージャtex.closetex;
var
t:テキスト;
始める
assign(t、namefl + '。tex');
追加(t);
writeln(t、 '\ end {document}');
閉じる(t);
終わり;
プロシージャtex.createpdf;
var
p:System.Diagnostics.Process;
始める
p:=新しいSystem.Diagnostics.Process();
p.StartInfo.FileName:= 'pdflatex';
p.StartInfo.Arguments:= namefl + '。tex';
p.Start();
終わり;
プロシージャtex.openpdf;
var
p:System.Diagnostics.Process;
始める
p:=新しいSystem.Diagnostics.Process();
p.StartInfo.FileName:= namefl + '。pdf';
p.Start();
終わり;
namefl:文字列;
プロシージャnewtex(s:文字列);
プロシージャの追加(s:文字列);
プロシージャclosetex;
プロシージャcreatepdf;
手順openpdf;
終わり;
実装
プロシージャtex.newtex(s:文字列);
var
t:テキスト;
始める
namefl:= s;
assign(t、s + '。tex');
書き換え(t);
writeln(t、 '\ documentclass [12pt] {article}');
writeln(t、 '\ usepackage {amsmath}');
writeln(t、 '%\ usepackage [rus] {babel}');
writeln(t、 '%\ usepackage [cp1251] {inputenc}');
writeln(t、 '\ begin {document}');
閉じる(t);
終わり;
プロシージャtex.add(s:文字列);
var
t:テキスト;
始める
assign(t、namefl + '。tex');
追加(t);
writeln(t、 '\ [');
writeln(t、s);
writeln(t、 '\]');
閉じる(t);
終わり;
プロシージャtex.closetex;
var
t:テキスト;
始める
assign(t、namefl + '。tex');
追加(t);
writeln(t、 '\ end {document}');
閉じる(t);
終わり;
プロシージャtex.createpdf;
var
p:System.Diagnostics.Process;
始める
p:=新しいSystem.Diagnostics.Process();
p.StartInfo.FileName:= 'pdflatex';
p.StartInfo.Arguments:= namefl + '。tex';
p.Start();
終わり;
プロシージャtex.openpdf;
var
p:System.Diagnostics.Process;
始める
p:=新しいSystem.Diagnostics.Process();
p.StartInfo.FileName:= namefl + '。pdf';
p.Start();
終わり;
タスク概要
微分問題と積分問題は逆であるため、2つの問題に対して1つの回路のみが必要であるということを事前に予約します。
制限
数学的分析のコースの開始時に、制限(x-> infを使用)が最も頻繁に発生します:inf / inf、0/0、inf-inf、a / infおよびa / b。
したがって、そのようなタスクのスキームでは、違いの
1.答えがゼロの例
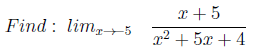
xはルートP1(x)(およびP2(x)のルートではない)に向かう傾向があるため、タスクはタイプP1(x)/ P2(x)*に従って構築されます。
* P1(x)およびP2(x)は、1から3(時には4番目)度の根を持つ多項式です(ランダム生成)
2.分母のゼロ
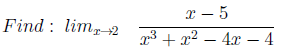
簡単です。 最初の例との類推により、分母のゼロはここにあります。
3.分子と分母のゼロ
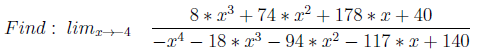
両方のP(x)が1つの根を持つように、根を持つ2つの多項式が構築されます。 次に、xがこのルートに向かうにつれて、比率0/0になります。 したがって、正しい答えを見つけるためにP1(x)とP2(x)を区別する必要があります。
4.無限大から無限大
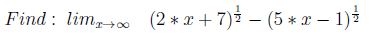
ルートの例を使用して、inf-infの原理による例を示すことにしました(多くの場合、本で見つかりましたが、他の例もあります)。
ここでは、P3(x)*とP4(x)*は同じ次数であり、解は共役で乗算および除算することに基づいています。
* P3(x)、P4(x)-1次の根の下の多項式
デリバティブと積分
「テイクアンドカウント」

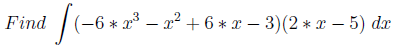
例は次のように構成されています。関数の微分が取得され(多項式/三角関数)、その積分(実際には、最初に取得された関数)を見つける必要があります。
Cな方法
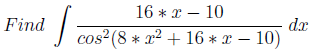
タスクはさまざまな方法で構築できます。 それらの1つは、三角関数T(P(x))(P(x)は2次以上の多項式)を取り、T(P(x))に微分P(x)を掛けます。 積分の拡張を使用しないために、そのようなテクニックに気づくことができなければなりません。
タスク生成コード
ユニットtaskMath;
インターフェース
mathUnitを使用します。
タイプtaskderivative = record
タスク:文字列。
答え:文字列。
終わり;
タイプtasklimits = record
タスク:文字列。
答え:文字列。
終わり;
関数taskintegral1(var s:string):文字列;
function tasklimits1(var s:string):文字列;
関数tasklimits2(var s:string):文字列;
function tasklimits3(var s:string):文字列;
function tasklimits4(var s:string):文字列;
関数taskderivative1(var s:string):文字列;
function taskderivative2(var s:string):文字列;
手続きrand(var x:taskderivative);
手続きrand(var x:tasklimits);
実装
関数が正しい(s:文字列):文字列;
var i:整数;
始める
for i:= 1からlength(s)まで
のケース[i]
'{':s [i]:= '(';
'}':s [i]:= ')';
終わり;
結果:= s;
終わり;
function tasklimits1(var s:string):文字列;
var
p1、p2:rootを伴う多項式;
i:整数;
x:整数;
rez:文字列;
k1、k2、r1、r2:整数;
始める
ランダム化;
p1.roots(ランダム(1,3));
p2.roots(ランダム(1,3));
i:=ランダム(p1.st)-1;
for i:= i downto 0 do
p2.root [ランダム(p2.st)]:= p1.root [ランダム(p1.st)];
i:=ランダム(p1.st)+ランダム(p2.st);
if(i> p1.st-1)then
始める
x:= p2.root [i-(p1.st-1)];
終わり
他に
x:= p1.root [i];
p1.nw;
p2.nw;
rez:= '検索:\; lim_ {x \ to \!' '' + inttostr(x)+ '} \ quad \ frac {' + p1.pltostr + '} {' + p2.pltostr + '}';
k1:= 0;
k2:= 0;
r1:= 1;
r2:= 1;
s:= '\の場合 略語\;(x-'+ inttostr(x)+')\; \; ';
for i:= 0 to p1.st-1 do
if(p1.kof [i] = x)then
inc(k1)
他に
r1:= r1 *(x-p1.kof [i]);
for i:= 0 to p2.st-1 do
if(p2.kof [i] = x)then
inc(k2)
他に
r2:= r2 *(x-p2.kof [i]);
if(k1> k2)then
s:= '0'; // s:= s + 'zero';
if(k2> k1)then
s:= 'inf'; // s:= s + 'zero \; \; 分母\; および\; \; 無限大 ';
if(k1 = k2)then
s:= inttostr(r1)+ '/' + inttostr(r2); // s:= s + 'number \;' + floattostr(r1 / r2);
s:=正しい(s);
結果:= rez;
終わり;
関数tasklimits2(var s:string):文字列;
var
f:ルートの多項式;
g、x:多項式;
st:整数;
rez、answ:文字列。
始める
f.roots(ランダム(1,2));
g.nw(ランダム(1,2));
x.nw(ランダム(1,2));
st:= f.root [random(0、f.st-1)];
rez:= '検索:\; lim_ {x \ to \!' '' inttostr(st)+ '} \ quad \ frac {' +(f * g).pltostr + '} {' +(f * x).pltostr + '}';
s:= floattostr(g.into(st))+ '/' + floattostr(x.into(st));
s:=正しい(s);
結果:= rez;
終わり;
function tasklimits3(var s:string):文字列;
var
f、g:sqrnpolynomial;
x:多項式;
rez、answ:文字列。
始める
f.nw(ランダム(1,4)、2);
g.nw(fxst、2);
x:= fx-gx;
rez:= '検索:\; lim_ {x \ to \ infty} \ quad' + f.s + '-' + gs;
if(x.st + 1 = fxst)then
s:= floattostr(x.kof [x.st])+ '/' + floattostr(gxkof [gxst] + fxkof [gxst])
他に
s:= '0';
s:=正しい(s);
結果:= rez;
終わり;
function tasklimits4(var s:string):文字列;
var
f、g:polynomialwithroot;
kf1、kf2:多項式;
a、i、j、num:整数;
rez、追加:文字列;
始める
f.roots(ランダム(1,2));
g.roots(random((f.st)、3));
num:=ランダム(1、f.st-1);
for i:= 0からnum-1 do
g.root [i]:= f.root [i];
g.nw;
// writeln(num);
睡眠(1000);
num:= 0;
for i:= 0 to f.st-1 do
for j:= 0 to g.st-1 do
if(f.kof [i] = g.kof [j])then num + = 1;
// writeln(num);
//スリープ(1000);
kf1.nw(ランダム(1,2));
kf2.nw(0);
a:=ランダム(2,5);
追加:= '\ frac {' +(kf1 + kf2).pltostr + '} {' + kf1.pltostr + '}';
for i:= 1からlength(s)まで
if(add [i] = 'x')then add [i]:= 'n';
rez:= '\を検索; x、\; いつ:\; lim_ {n \ to \ infty} \ quad '+
add + '\ frac {(' + f.pltostr + ')^ {n ^' + inttostr(a)+ '}} {(' + g.pltostr + ')^ {n ^' + inttostr(a)+ '}} = e ^ {'+ floattostr(kf2.kof [0])+'} ';
s:= inttostr(num);
結果:= rez;
終わり;
関数taskintegral1(var s:string):文字列;
var
tr1:sinx;
tr2:cosx;
tr3:tgx;
tr4:ctgx;
f、g:多項式;
r:整数;
rez:文字列;
始める
rez:= 'Find \; \ int';
r:=ランダム(1,5);
のケースr
1:始める
tr1.x.nw(ランダム(1,3));
tr1.nw;
s:= tr1.s;
tr1.derivative;
rez:= rez + tr1.s + '\; dx';
終わり;
2:始める
tr2.x.nw(ランダム(1,3));
tr2.nw;
s:= tr2.s;
tr2.derivative;
rez:= rez + tr2.s + '\; dx';
終わり;
3:始める
tr3.x.nw(ランダム(1,3));
tr3.nw;
s:= tr3.s;
tr3.derivative;
rez:= rez + tr3.s + '\; dx';
終わり;
4:始める
tr4.x.nw(ランダム(1,3));
tr4.nw;
s:= tr4.s;
tr4.derivative;
rez:= rez + tr4.s + '\; dx';
終わり;
5:開始
r:=ランダム(1,2);
f.nw(ランダム(1,3));
rez:= rez + '(' + f.pltostr + ')';
while(r <> 0)do
始める
g.nw(ランダム(1,3));
f:= f * g;
rez:= rez + '(' + g.pltostr + ')';
r:= r-1;
終わり;
f.integral;
s:=正しい(f.pltostr);
rez:= rez + '\; dx';
終わり;
終わり;
s:=正しい(s);
結果:= rez;
終わり;
関数taskderivative1(var s:string):文字列;
var
sinx1、sinx2:sinx;
cosx1、cosx2:cosx;
tgx1、tgx2:tgx;
ctgx1、ctgx2:ctgx;
f、g:多項式;
r:整数;
rez:文字列;
bg、answ:文字列;
始める
ランダム化;
sinx1.x.nw(ランダム(1,3));
sinx1.nw;
sinx2:= sinx1;
sinx2.derivative;
tgx1.x.nw(ランダム(1,3));
tgx1.nw;
tgx2:= tgx1;
tgx2.derivative;
cosx1.x.nw(ランダム(1,3));
cosx1.nw;
cosx2:= cosx1;
cosx2.derivative;
ctgx1.x.nw(ランダム(1,3));
ctgx1.nw;
ctgx2:= ctgx1;
ctgx2.derivative;
r:=ランダム(1,4);
のケースr
1:始める
rez:= rez + sinx1.s;
answ:= sinx2.s;
終わり;
2:始める
rez:= rez + cosx1.s;
answ:= cosx2.s;
終わり;
3:始める
rez:= rez + tgx1.s;
answ:= '(' + tgx2.x.pltostr + ')/(cos(' + tgx1.x.pltostr + ')^ 2)';
終わり;
4:始める
rez:= rez + ctgx1.s;
answ:= '(' +(-1 * ctgx2.x).pltostr + '))/(sin(' + ctgx1.x.pltostr + ')^ 2)';
終わり;
終わり;
bg:= rez;
rez:= '\を検索; \ frac {d} {dx} \;( '+ rez;
rez:= rez + ')';
r:=ランダム(1,2);
f.nw(ランダム(1,3));
while(r> 0)do
始める
g.nw(ランダム(1,3));
rez:= rez + '(';
rez:= rez + g.pltostr;
rez:= rez + ')';
f:= f * g;
r:= r-1;
終わり;
rez:= rez + ')';
answ:= '(' + answ + ')*(' + g.pltostr + ')+(';
g.derivative;
answ:= answ + bg + ')*(' + g.pltostr + ')';
s:= answ;
s:=正しい(s);
結果:= rez;
終わり;
function taskderivative2(var s:string):文字列;
var
sinx1、sinx2:sinx;
cosx1、cosx2:cosx;
tgx1、tgx2:tgx;
ctgx1、ctgx2:ctgx;
f、g、st:多項式;
r:整数;
rez:文字列;
answering、bg:string;
始める
ランダム化;
sinx1.x.nw(ランダム(1,3));
sinx1.nw;
sinx2:= sinx1;
sinx2.derivative;
tgx1.x.nw(ランダム(1,3));
tgx1.nw;
tgx2:= tgx1;
tgx2.derivative;
cosx1.x.nw(ランダム(1,3));
cosx1.nw;
cosx2:= cosx1;
cosx2.derivative;
ctgx1.x.nw(ランダム(1,3));
ctgx1.nw;
ctgx2:= ctgx1;
ctgx2.derivative;
r:=ランダム(1,4);
のケースr
1:始める
rez:= rez + sinx1.s;
answ:= sinx2.s;
終わり;
2:始める
rez:= rez + cosx1.s;
answ:= cosx2.s;
終わり;
3:始める
rez:= rez + tgx1.s;
answ:= '(' + tgx2.x.pltostr + ')/(cos(' + tgx1.x.pltostr + ')^ 2)';
終わり;
4:始める
rez:= rez + ctgx1.s;
answ:= '(' +(-1 * ctgx2.x).pltostr + '))/(sin(' + ctgx1.x.pltostr + ')^ 2)';
終わり;
終わり;
bg:= rez;
rez:= '\を検索; \ frac {d} {dx} \;( '+ rez;
rez:= rez + ')^ {';
f.nw(ランダム(1,3));
rez:= rez + f.pltostr + '}';
st:= f;
st.derivative;
answ:= '((' + bg + ')^ {' + f.pltostr + '})*((' + st.pltostr + ')* ln(' + bg + ')+(' + f.pltostr + ')*( '+ answ +')/( '+ bg +') ';
s:= answ;
s:=正しい(s);
結果:= rez;
終わり;
手続きrand(var x:taskderivative);
var
r:整数;
始める
ランダム化;
r:=ランダム(1,2);
のケースr
1:x.task:= taskderivative1(x.answer);
2:x.task:= taskderivative2(x.answer);
終わり;
終わり;
手続きrand(var x:tasklimits);
var
r:整数;
始める
ランダム化;
r:=ランダム(1,4);
のケースr
1:x.task:= tasklimits1(x.answer);
2:x.task:= tasklimits2(x.answer);
3:x.task:= tasklimits3(x.answer);
4:x.task:= tasklimits4(x.answer);
終わり;
終わり;
終わり。
インターフェース
mathUnitを使用します。
タイプtaskderivative = record
タスク:文字列。
答え:文字列。
終わり;
タイプtasklimits = record
タスク:文字列。
答え:文字列。
終わり;
関数taskintegral1(var s:string):文字列;
function tasklimits1(var s:string):文字列;
関数tasklimits2(var s:string):文字列;
function tasklimits3(var s:string):文字列;
function tasklimits4(var s:string):文字列;
関数taskderivative1(var s:string):文字列;
function taskderivative2(var s:string):文字列;
手続きrand(var x:taskderivative);
手続きrand(var x:tasklimits);
実装
関数が正しい(s:文字列):文字列;
var i:整数;
始める
for i:= 1からlength(s)まで
のケース[i]
'{':s [i]:= '(';
'}':s [i]:= ')';
終わり;
結果:= s;
終わり;
function tasklimits1(var s:string):文字列;
var
p1、p2:rootを伴う多項式;
i:整数;
x:整数;
rez:文字列;
k1、k2、r1、r2:整数;
始める
ランダム化;
p1.roots(ランダム(1,3));
p2.roots(ランダム(1,3));
i:=ランダム(p1.st)-1;
for i:= i downto 0 do
p2.root [ランダム(p2.st)]:= p1.root [ランダム(p1.st)];
i:=ランダム(p1.st)+ランダム(p2.st);
if(i> p1.st-1)then
始める
x:= p2.root [i-(p1.st-1)];
終わり
他に
x:= p1.root [i];
p1.nw;
p2.nw;
rez:= '検索:\; lim_ {x \ to \!' '' + inttostr(x)+ '} \ quad \ frac {' + p1.pltostr + '} {' + p2.pltostr + '}';
k1:= 0;
k2:= 0;
r1:= 1;
r2:= 1;
s:= '\の場合 略語\;(x-'+ inttostr(x)+')\; \; ';
for i:= 0 to p1.st-1 do
if(p1.kof [i] = x)then
inc(k1)
他に
r1:= r1 *(x-p1.kof [i]);
for i:= 0 to p2.st-1 do
if(p2.kof [i] = x)then
inc(k2)
他に
r2:= r2 *(x-p2.kof [i]);
if(k1> k2)then
s:= '0'; // s:= s + 'zero';
if(k2> k1)then
s:= 'inf'; // s:= s + 'zero \; \; 分母\; および\; \; 無限大 ';
if(k1 = k2)then
s:= inttostr(r1)+ '/' + inttostr(r2); // s:= s + 'number \;' + floattostr(r1 / r2);
s:=正しい(s);
結果:= rez;
終わり;
関数tasklimits2(var s:string):文字列;
var
f:ルートの多項式;
g、x:多項式;
st:整数;
rez、answ:文字列。
始める
f.roots(ランダム(1,2));
g.nw(ランダム(1,2));
x.nw(ランダム(1,2));
st:= f.root [random(0、f.st-1)];
rez:= '検索:\; lim_ {x \ to \!' '' inttostr(st)+ '} \ quad \ frac {' +(f * g).pltostr + '} {' +(f * x).pltostr + '}';
s:= floattostr(g.into(st))+ '/' + floattostr(x.into(st));
s:=正しい(s);
結果:= rez;
終わり;
function tasklimits3(var s:string):文字列;
var
f、g:sqrnpolynomial;
x:多項式;
rez、answ:文字列。
始める
f.nw(ランダム(1,4)、2);
g.nw(fxst、2);
x:= fx-gx;
rez:= '検索:\; lim_ {x \ to \ infty} \ quad' + f.s + '-' + gs;
if(x.st + 1 = fxst)then
s:= floattostr(x.kof [x.st])+ '/' + floattostr(gxkof [gxst] + fxkof [gxst])
他に
s:= '0';
s:=正しい(s);
結果:= rez;
終わり;
function tasklimits4(var s:string):文字列;
var
f、g:polynomialwithroot;
kf1、kf2:多項式;
a、i、j、num:整数;
rez、追加:文字列;
始める
f.roots(ランダム(1,2));
g.roots(random((f.st)、3));
num:=ランダム(1、f.st-1);
for i:= 0からnum-1 do
g.root [i]:= f.root [i];
g.nw;
// writeln(num);
睡眠(1000);
num:= 0;
for i:= 0 to f.st-1 do
for j:= 0 to g.st-1 do
if(f.kof [i] = g.kof [j])then num + = 1;
// writeln(num);
//スリープ(1000);
kf1.nw(ランダム(1,2));
kf2.nw(0);
a:=ランダム(2,5);
追加:= '\ frac {' +(kf1 + kf2).pltostr + '} {' + kf1.pltostr + '}';
for i:= 1からlength(s)まで
if(add [i] = 'x')then add [i]:= 'n';
rez:= '\を検索; x、\; いつ:\; lim_ {n \ to \ infty} \ quad '+
add + '\ frac {(' + f.pltostr + ')^ {n ^' + inttostr(a)+ '}} {(' + g.pltostr + ')^ {n ^' + inttostr(a)+ '}} = e ^ {'+ floattostr(kf2.kof [0])+'} ';
s:= inttostr(num);
結果:= rez;
終わり;
関数taskintegral1(var s:string):文字列;
var
tr1:sinx;
tr2:cosx;
tr3:tgx;
tr4:ctgx;
f、g:多項式;
r:整数;
rez:文字列;
始める
rez:= 'Find \; \ int';
r:=ランダム(1,5);
のケースr
1:始める
tr1.x.nw(ランダム(1,3));
tr1.nw;
s:= tr1.s;
tr1.derivative;
rez:= rez + tr1.s + '\; dx';
終わり;
2:始める
tr2.x.nw(ランダム(1,3));
tr2.nw;
s:= tr2.s;
tr2.derivative;
rez:= rez + tr2.s + '\; dx';
終わり;
3:始める
tr3.x.nw(ランダム(1,3));
tr3.nw;
s:= tr3.s;
tr3.derivative;
rez:= rez + tr3.s + '\; dx';
終わり;
4:始める
tr4.x.nw(ランダム(1,3));
tr4.nw;
s:= tr4.s;
tr4.derivative;
rez:= rez + tr4.s + '\; dx';
終わり;
5:開始
r:=ランダム(1,2);
f.nw(ランダム(1,3));
rez:= rez + '(' + f.pltostr + ')';
while(r <> 0)do
始める
g.nw(ランダム(1,3));
f:= f * g;
rez:= rez + '(' + g.pltostr + ')';
r:= r-1;
終わり;
f.integral;
s:=正しい(f.pltostr);
rez:= rez + '\; dx';
終わり;
終わり;
s:=正しい(s);
結果:= rez;
終わり;
関数taskderivative1(var s:string):文字列;
var
sinx1、sinx2:sinx;
cosx1、cosx2:cosx;
tgx1、tgx2:tgx;
ctgx1、ctgx2:ctgx;
f、g:多項式;
r:整数;
rez:文字列;
bg、answ:文字列;
始める
ランダム化;
sinx1.x.nw(ランダム(1,3));
sinx1.nw;
sinx2:= sinx1;
sinx2.derivative;
tgx1.x.nw(ランダム(1,3));
tgx1.nw;
tgx2:= tgx1;
tgx2.derivative;
cosx1.x.nw(ランダム(1,3));
cosx1.nw;
cosx2:= cosx1;
cosx2.derivative;
ctgx1.x.nw(ランダム(1,3));
ctgx1.nw;
ctgx2:= ctgx1;
ctgx2.derivative;
r:=ランダム(1,4);
のケースr
1:始める
rez:= rez + sinx1.s;
answ:= sinx2.s;
終わり;
2:始める
rez:= rez + cosx1.s;
answ:= cosx2.s;
終わり;
3:始める
rez:= rez + tgx1.s;
answ:= '(' + tgx2.x.pltostr + ')/(cos(' + tgx1.x.pltostr + ')^ 2)';
終わり;
4:始める
rez:= rez + ctgx1.s;
answ:= '(' +(-1 * ctgx2.x).pltostr + '))/(sin(' + ctgx1.x.pltostr + ')^ 2)';
終わり;
終わり;
bg:= rez;
rez:= '\を検索; \ frac {d} {dx} \;( '+ rez;
rez:= rez + ')';
r:=ランダム(1,2);
f.nw(ランダム(1,3));
while(r> 0)do
始める
g.nw(ランダム(1,3));
rez:= rez + '(';
rez:= rez + g.pltostr;
rez:= rez + ')';
f:= f * g;
r:= r-1;
終わり;
rez:= rez + ')';
answ:= '(' + answ + ')*(' + g.pltostr + ')+(';
g.derivative;
answ:= answ + bg + ')*(' + g.pltostr + ')';
s:= answ;
s:=正しい(s);
結果:= rez;
終わり;
function taskderivative2(var s:string):文字列;
var
sinx1、sinx2:sinx;
cosx1、cosx2:cosx;
tgx1、tgx2:tgx;
ctgx1、ctgx2:ctgx;
f、g、st:多項式;
r:整数;
rez:文字列;
answering、bg:string;
始める
ランダム化;
sinx1.x.nw(ランダム(1,3));
sinx1.nw;
sinx2:= sinx1;
sinx2.derivative;
tgx1.x.nw(ランダム(1,3));
tgx1.nw;
tgx2:= tgx1;
tgx2.derivative;
cosx1.x.nw(ランダム(1,3));
cosx1.nw;
cosx2:= cosx1;
cosx2.derivative;
ctgx1.x.nw(ランダム(1,3));
ctgx1.nw;
ctgx2:= ctgx1;
ctgx2.derivative;
r:=ランダム(1,4);
のケースr
1:始める
rez:= rez + sinx1.s;
answ:= sinx2.s;
終わり;
2:始める
rez:= rez + cosx1.s;
answ:= cosx2.s;
終わり;
3:始める
rez:= rez + tgx1.s;
answ:= '(' + tgx2.x.pltostr + ')/(cos(' + tgx1.x.pltostr + ')^ 2)';
終わり;
4:始める
rez:= rez + ctgx1.s;
answ:= '(' +(-1 * ctgx2.x).pltostr + '))/(sin(' + ctgx1.x.pltostr + ')^ 2)';
終わり;
終わり;
bg:= rez;
rez:= '\を検索; \ frac {d} {dx} \;( '+ rez;
rez:= rez + ')^ {';
f.nw(ランダム(1,3));
rez:= rez + f.pltostr + '}';
st:= f;
st.derivative;
answ:= '((' + bg + ')^ {' + f.pltostr + '})*((' + st.pltostr + ')* ln(' + bg + ')+(' + f.pltostr + ')*( '+ answ +')/( '+ bg +') ';
s:= answ;
s:=正しい(s);
結果:= rez;
終わり;
手続きrand(var x:taskderivative);
var
r:整数;
始める
ランダム化;
r:=ランダム(1,2);
のケースr
1:x.task:= taskderivative1(x.answer);
2:x.task:= taskderivative2(x.answer);
終わり;
終わり;
手続きrand(var x:tasklimits);
var
r:整数;
始める
ランダム化;
r:=ランダム(1,4);
のケースr
1:x.task:= tasklimits1(x.answer);
2:x.task:= tasklimits2(x.answer);
3:x.task:= tasklimits3(x.answer);
4:x.task:= tasklimits4(x.answer);
終わり;
終わり;
終わり。
まとめ
多種多様な典型的な手法と例がありますが、資料を理解するための最小限の評価のために、そのようなセットは数回助けになりました。 もちろん、このセットは拡張および拡張できますが、これはすべての人のビジネスです。
プログラムへのリンク: GitHub
そのプロジェクトには他のタスクがありますが、それらの混合作業(テストと更新)のためにこの記事では説明していません。