🤶🏼 🕺🏾 🆎 なぜHo-Kashyapアルゴリズムが必要なのですか？ 🥘 🆖 🔷

最近、Ha -Kashyapアルゴリズム（Ho-Kashyap手続き、別名-NSCEのアルゴリズム、最小標準誤差）に関する出版物がHabréに掲載されました。私にはあまりはっきりしていないように思えたので、自分で考え出すことにしました。このトピックはロシア語を話すインターネットではあまり理解されていないことがわかったため、検索の結果に基づいて記事を書くことにしました。

機械学習におけるニューラルネットワークのブームにもかかわらず、線形分類アルゴリズムの使用と解釈はずっと簡単です。しかし同時に、サポートベクターメソッドやロジスティック回帰などの高度なメソッドを使用したくない場合もあります。また、すべてのデータを1つの大きな線形最小二乗回帰に入れたいという誘惑があります。さらに、MS Excelでも完全に構築できます。

このアプローチの問題は、入力データが線形に分離可能である場合でも、結果の分類器がそれらを分離しない可能性があることです。たとえば、ポイントのセットの場合 $X = [（6、9）、（5、7）、（5、9）、（10、1）]$ 、 $y = [1、1、-1、-1]$ 分割線を取得します $（0.15x_1-0.43x_2 + 3.21）= 0$ （例は（1）から借用しています）：

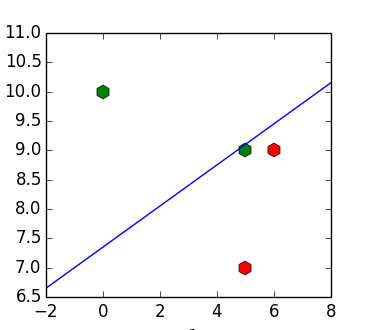
疑問が生じます-何らかの形でこの行動の特徴を取り除くことは可能ですか？

線形分類問題

まず、記事の主題を形式化します。

ダナ行列 $X$ 各行 $X_i$ オブジェクトの特性記述に対応します $私は$ （定数を含む $1$ ）およびクラスラベルベクトル $y$ どこで $y_i \ in \ {+ 1、-1 \}$ -オブジェクトラベル $私は$ 。次の形式の線形分類器を構築したい $符号（Xw）= y$ 。

>>> import numpy as np >>> X = np.array([[6, 9, 1], [5, 7, 1], [5, 9, 1], [0, 10, 1]]) >>> y = np.array([[1], [1], [-1], [-1]])

これを行う最も簡単な方法は、OLS回帰を構築することです $Xw = y$ つまり、偏差の二乗の合計を最小化します $\ min \ sum（w X_i-y_i）^ 2$ 。最適な重量は次の式で見つけることができます $w = X ^ {+} y$ どこで $X ^ {+}$ 擬似逆行列です。したがって、記事の最初から写真が取得されます。

 >>> w = np.dot(np.linalg.pinv(X), y) >>> w array([[ 0.15328467], [-0.4379562 ], [ 3.2189781 ]]) >>> np.dot(X, w) array([[ 0.19708029], [ 0.91970803], [ 0.04379562], [-1.16058394]])

線形分離可能性

記述の便宜上、各不等式を要素ごとに乗算します $Xw = y$ に $y$ 左側で取得した行列を呼び出します $Y = y \倍X$ （こちら $\回$ 行ごとの乗算を意味します）。次に、OLS回帰の条件は $Yw = 1$ 、最小化の問題は最小化することです $\ min \ sum（w Y_i-1）^ 2$ 。

 >>> Y = y * X >>> Y array([[ 6, 9, 1], [ 5, 7, 1], [ -5, -9, -1], [ 0, -10, -1]])

この時点で、クラスの分離の条件は $符号（Xw）= y$ または $符号（Yw）= 1$ 、そしてクラスを分離したいので、この問題を解決する必要があります。

ベクターを導入 $b$ その中で $b_i$ 要素からの距離を担当します $私は$ 分割線（ $Yw = b$ ）すべての要素を正しく分類するため、条件を導入します $b＆gt; 0$ 。その後、問題は $\ min \ sum（w Y_i-b_i）^ 2$ そしてどのように決定されます $w = Y ^ {+} y$ 。これらの値を手動で選択できます $b$ 結果のプレーンがサンプルを共有すること：

 >>> b = np.ones([4, 1]) >>> b[3] = 10 >>> w = np.dot(np.linalg.pinv(Y), b) >>> np.dot(Y, w) array([[ 0.8540146 ], [ 0.98540146], [ 0.81021898], [ 10.02919708]])

Ho Kashyapアルゴリズム

Ho Kashyapアルゴリズムは、 $b$ 自動的に。アルゴリズムスキーム（ $k$ -ステップ番号 $b ^ {（0）}$ 通常平等に取られる $1$ ）：

OLS回帰係数を計算します（ $w ^ {（k）} = Y ^ {+} b ^ {（k）}$ ）
インデントベクトルを計算する $b ^ {（k + 1）}$ 。
決定が同意しない場合（ $b ^ {（k）} \ neq b ^ {（k + 1）}$ ）、ステップ1を繰り返します。

何らかの方法で計算したいインデントベクトル $b ^ {（k + 1）} = \ max（Yw ^ {（k）}、0）$ これにより損失関数が最小化されるため $\ min \ sum（w Y_i-b_i）^ 2$ 。残念ながら、条件 $b＆gt; 0$ これを行うことを防ぎ、代わりに損失関数の勾配の正の部分に沿って一歩を踏み出すことが提案されています $e ^ {（k）} = b ^ {k}-Yw ^ {（k）}$ ： $b ^ {（k + 1）} = b ^ {（k）}-\ mu（e ^ {（k）}-| e ^ {k} |）$ どこで $\ mu$ -ステップ勾配降下、問題を解決する過程で減少します。

 >>> e = -np.inf * np.ones([4, 1]) >>> b = np.ones([4, 1]) >>> while np.any(e < 0): ... w = np.dot(np.linalg.pinv(Y), b) ... e = b - np.dot(Y, w) ... b = b - e * (e < 0) ... >>> b array([[ 1.], [ 1.], [ 1.], [ 12.]]) >>> w array([[ 2.], [-1.], [-2.]])

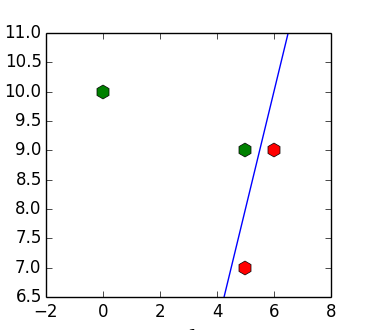
線形に分離可能なサンプルの場合、アルゴリズムは常に分離平面に収束し、収束します（すべての勾配要素が $b$ 非負の場合、それらはすべてゼロです）。

線形に分離できないサンプルの場合、損失関数は任意に小さくできます。 $b$ そして $w$ 値を変更する定数に変更します。原則として、アルゴリズムは収束しない場合があります。検索では、このトピックに関する特定の推奨事項は提供されません。

Ho-Kashyapアルゴリズムと線形SVMの接続

オブジェクトが正しく分類されていれば、提起された最適化問題のエラー（ $\ min \ sum_ {i}（w Y_i-b_i）^ 2$ ）そのエラーをゼロに減らすことができます。オブジェクトが誤って分類されている場合、そのオブジェクトの最小エラーは、分割線からのインデントの二乗に等しくなります（ $（w Y_i）^ 2$ ）次に、損失関数を次の形式で書き直すことができます。

$\ min_ {w} \ sum_ {i} \ max（0、1-w Y_i）^ 2-2 \ max（0、1-w Y_i）$

また、線形SVM損失関数の形式は次のとおりです。

$\ min_ {w} \ lambda || w || ^ 2 + \ frac {1} {N} \ sum_ {i} \ max（0、1-w Y_i）$

したがって、Ho-Kashyapアルゴリズムによって解決される問題は、2次損失関数（分離平面から遠く離れた放射に対してより細かく罰金を科す）と分離ストリップの幅を無視する（つまり、最も近い場所から可能な限り離れた非平面を探す）正しく分類された要素、および任意の分割面）。

多次元の場合

MNC回帰は、フィッシャーの 2クラス線形判別式の類似物であることを思い出してください（それらの解は定数まで一致します）。 Ho-Kashpyapアルゴリズムはケースにも適用できます $K$ クラス-これ $w$ そして $b$ 行列になる $W$ そして $B$ サイズ $D \回K$ そして $N \回K$ ここで、それぞれ $D$ 問題の次元であり、 $N$ -オブジェクトの数。この場合、誤ったクラスに対応する列には負の値が必要です。

謝辞

便利なエディターのparpalak 。

オリジナル記事のrocket3 。

参照資料

（1） http://www.csd.uwo.ca/~olga/Courses/CS434a_541a/Lecture10.pdf

（2） http://research.cs.tamu.edu/prism/lectures/pr/pr_l17.pdf

（3） http://web.khu.ac.kr/~tskim/PatternClass Lec Note 07-1.pdf

（4）A.E. レプスキー、A.G。 Bronevich パターン認識のための数学的方法。 講座

（5）Tu J.、ゴンザレスR. パターン認識の原理

（6）R. Duda、P。Hart パターン認識およびシーン分析

なぜHo-Kashyapアルゴリズムが必要なのですか？