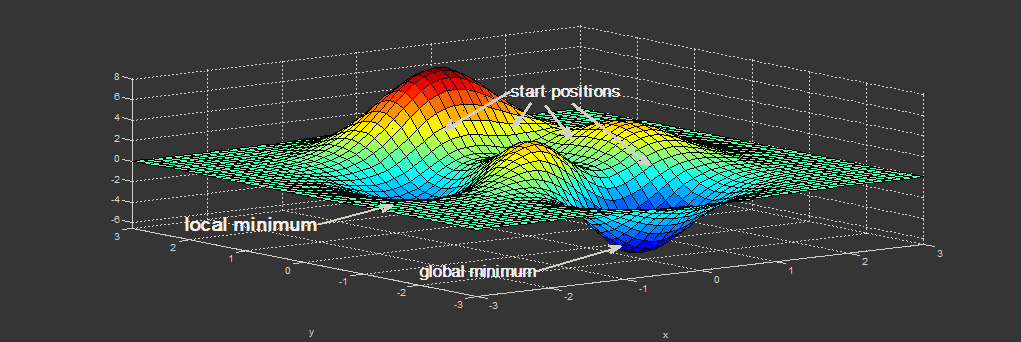
👩🏾 🙆 👩🏾‍🤝‍👩🏼 Levenberg-非線形最小二乗法のMarquardtアルゴリズムとPythonでの実装 💪🏼 🤳🏿 📭

目的関数の極値（最小または最大）を見つけることは、数学とその応用における重要なタスクです（特に、機械学習には曲線近似の問題があります）。確かに誰もが最急降下法（MHC）とニュートン法（MH）について聞いた。残念ながら、これらの方法には多くの重大な欠点があります。特に、最急降下法は最適化の終了時に非常に長い時間収束する可能性があり、ニュートン法では2次導関数の計算が必要であり、多くの計算が必要です。

多くの場合に発生する欠点を解消するには、サブジェクト領域をさらに深く掘り下げ、入力データに制限を追加する必要があります。特に、MHCとMHは任意の機能を処理します。統計および機械学習では、多くの場合、最小二乗法（OLS）に対処する必要があります。この方法は、二乗誤差の合計を最小化します。目的関数は次のように表されます

$\ frac {1} {2} \ sum \ limits_ {i = 1} ^ {N}（y_i'-y_i）^ 2 = \ frac {1} {2} \ sum \ limits_ {i = 1} ^ {N } r_i ^ 2 \タグ{1}$

Levenberg-Marquardtアルゴリズムは、非線形最小二乗法です。記事には以下が含まれます。

アルゴリズムの説明
メソッドの説明：最急降下、ニュートン、ガウス-ニュートン
githubのソースコードを使用したPythonの実装
メソッド比較

コードは、 numpy、matplotlibなどの追加のライブラリを使用します。それらがない場合は、 Anaconda for Pythonからインストールすることを強くお勧めします。

依存関係

Levenberg-Marquardtアルゴリズムは、フローチャートに示された方法に依存しています

したがって、最初にそれらを勉強する必要があります。これをします

定義

$F = F（x）$ -ターゲット関数。最小化します $F$ 。この場合、 $F$ 損失の関数です
$\ nabla f（x）$ -関数勾配 $f$ その時点で $x$
$x ^ *$ - $x$ どこで $F（x ^ *）$ は極小値、つまりパンクした近所がある場合 $\ドット{U}（x）$ そのような $\ forall x \ in \ dot {U}（x）\ \ \ F（x ^ *）\ le F（x）$
$x ^ +$ -グローバル最小 $\ forall x \ in R ^ n \ \ \ F（x ^ +）\ le F（x）$ 、つまり $F$ 関係ありません $F（x ^ +）$
$J_f = J_f（x）= J$ -関数のヤコビ行列 $f：R ^ n \からR ^ m$ その時点で $x$ 。つまりこれは、すべての一次偏導関数の表です。実際、これは次の勾配の類似物です。 $f：R ^ n \からR$ 、この場合はからのマッピングを扱っているため $n$ 次元ベクトル $m$ 次元であるため、勾配で発生するように、1次元で1次導関数を計算することはできません。詳細
$H_f = H_f（x）= H$ - ヘッセ行列（2次導関数の行列）。二次近似に必要

機能選択

数学的最適化には、新しいメソッドがテストされる関数があります。

そのような関数の1つがRosenbrock Functionです。 2つの変数の関数の場合、次のように定義されます

$f（x、y）=（ax）^ 2 + b（yx ^ 2）^ 2$

受け入れました $a = 0.5、\ b = 0.5$ 。つまり関数の形式は次のとおりです。

$f（x、y）= \ frac {1} {2}（1-x）^ 2 + \ frac {1} {2}（yx ^ 2）^ 2$

間隔での関数の動作を検討します $-2 \ le x、y \ le 2$

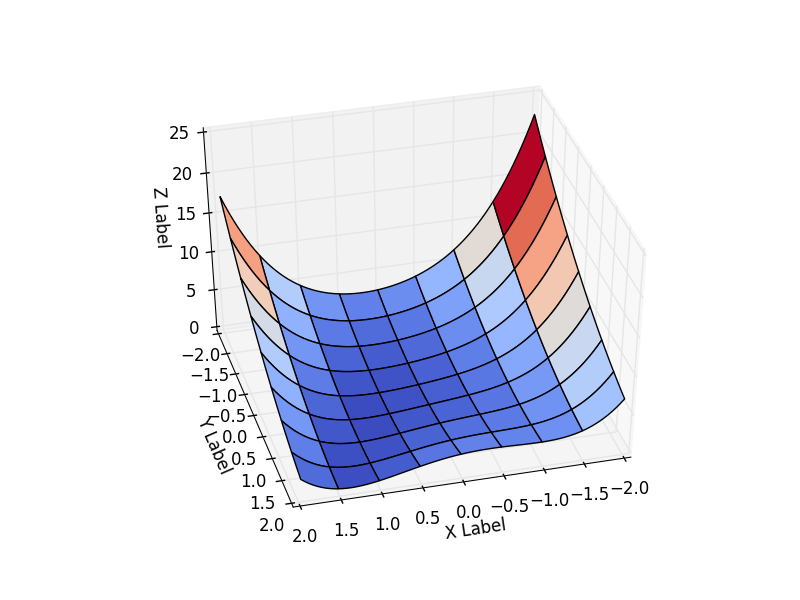
この関数は非負で定義され、最小値を持ちます $ポイントト$（x = 1、y = 1）でz = 0 $$

コードでは、関数に関するすべてのデータを1つのクラスにカプセル化し、必要な関数のクラスを取得する方が簡単です。結果は、最適化の開始点によって異なります。彼女を選ぶ $（X = -2、y = -2）$ 。グラフからわかるように、この時点で関数は間隔の最大値を取ります。

functions.py

class Rosenbrock: initialPoint = (-2, -2) camera = (41, 75) interval = [(-2, 2), (-2, 2)] """   """ @staticmethod def function(x): return 0.5*(1-x[0])**2 + 0.5*(x[1]-x[0]**2)**2 """    -  - r """ @staticmethod def function_array(x): return np.array([1 - x[0] , x[1] - x[0] ** 2]).reshape((2,1)) @staticmethod def gradient(x): return np.array([-(1-x[0]) - (x[1]-x[0]**2)*2*x[0], (x[1] - x[0]**2)]) @staticmethod def hesse(x): return np.array(((1 -2*x[1] + 6*x[0]**2, -2*x[0]), (-2 * x[0], 1))) @staticmethod def jacobi(x): return np.array([ [-1, 0], [-2*x[0], 1]]) """     : http://www.mathworks.com/help/matlab/matlab_prog/vectorization.html """ @staticmethod def getZMeshGrid(X, Y): return 0.5*(1-X)**2 + 0.5*(Y - X**2)**2

最急降下法

メソッド自体は非常に簡単です。受け入れる $F（x）= f（x）$ 、つまり目的関数は与えられたものと一致します。

見つける必要がある $d_ {ns}（x）$ -関数の最急降下の方向 $f$ その時点で $x$ 。

$f（x）$ で線形近似できます $x$ ：

$f（x + d）\約f（x）+ \ nabla f（x）^ Td、\ d \ in R ^ n、|| d || \ to 0 \タグ{2}$

$\ lim_ {d \ to 0} f（x）-f（x + d）=-\ nabla f（x）^ Td \ stackrel {（3.a）} =-|| \ nabla f（x）^ T || \ || d || cos \ theta、\タグ{3}$

どこで $\シータ$ ベクトル間の角度です $d \および\ nabla f（x）^ T$ 。 $（3.a）$ スカラー積から続く

それでは、最小化する方法 $f（x）$ そして、差が大きいほど $（3）$ より良い。で $\ theta = \ pi$ 式は最大化されます（ $cos \ theta = -1$ 、ベクトルのノルムは常に負ではありません）、および $\ theta = \ pi$ ベクトルの場合のみ $d \および\ \ nabla f（x）^ T$ したがって反対になります

$d_ {ns} =-\ nabla f（x）^ T$

私たちの方向は正しいが、一歩踏み込んでいる $|| d_ {ns} ||$ あなたは間違った道を行くことができます。一歩踏み出す：

$d_ {ns} =-\ alpha \ nabla f（x）^ T、0＆lt; \ alpha＆lt; 1$

理論的には、ステップが小さいほど良いです。しかし、その後、収束率が低下します。推奨値 $\アルファ= 0.05$

コードでは、次のようになります。まず、基本オプティマイザークラス。将来必要になるすべてのものを転送します（ヘシアンおよびヤコビ行列は現在必要ありませんが、他の方法には必要です）

 class Optimizer: def __init__(self, function, initialPoint, gradient=None, jacobi=None, hesse=None, interval=None, epsilon=1e-7, function_array=None, metaclass=ABCMeta): self.function_array = function_array self.epsilon = epsilon self.interval = interval self.function = function self.gradient = gradient self.hesse = hesse self.jacobi = jacobi self.name = self.__class__.__name__.replace('Optimizer', '') self.x = initialPoint self.y = self.function(initialPoint) "      " @abstractmethod def next_point(self): pass """     """ def move_next(self, nextX): nextY = self.function(nextX) self.y = nextY self.x = nextX return self.x, self.y

オプティマイザー自体のコード：

 class SteepestDescentOptimizer(Optimizer): ... def next_point(self): nextX = self.x - self.learningRate * self.gradient(self.x) return self.move_next(nextX)

最適化結果：

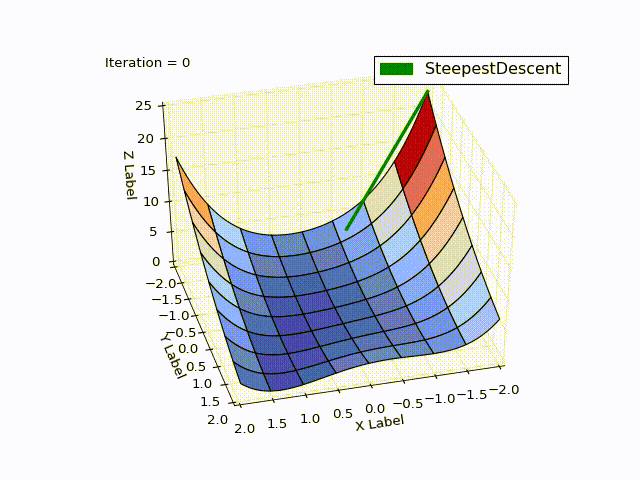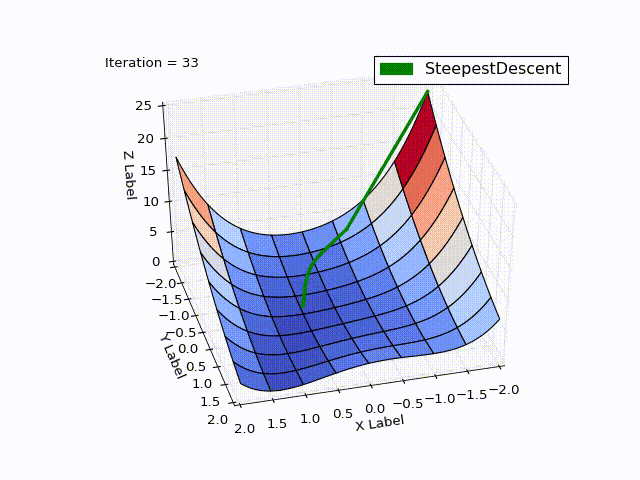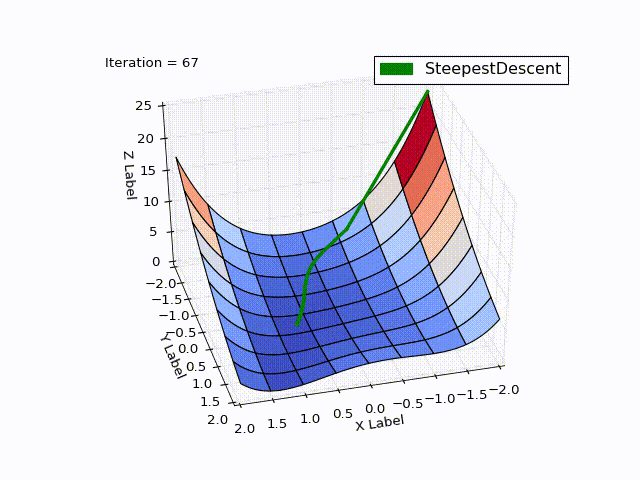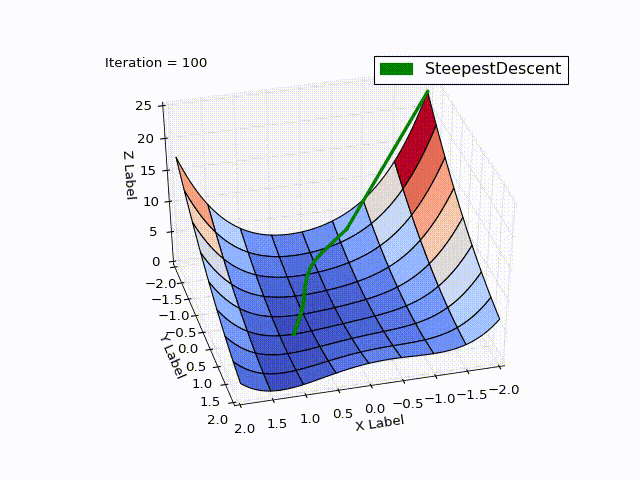
反復	X	Y	Z
25	0.383	-0.409	0.334
75	0.693	0.32	0.058
532	0.996	0.990	$10 ^ {-6}$

驚くべきことです。最適化は0〜25回の反復でどれだけ速く進行し、すでに25〜75回は遅く、最後にはゼロに近づくには457回の反復が必要でした。この動作はMHFの非常に特徴的なものです。最初は非常に良好な収束率で、最後は不十分です。

ニュートン法

ニュートン法自体は、方程式の根、つまりそのような $x$ あれ $f（x）= 0$ 。これはまさに私たちが必要とするものではありません、なぜなら関数には極値がある場合がありますが、必ずしもゼロではありません。

そして、最適化のためのニュートン法があります。最適化のコンテキストで人々がMNについて話すとき、それはそれを意味します。私自身、研究所で勉強している間、これらの方法を愚かさで混乱させ、「ニュートン法には欠点があります-二次導関数を考慮する必要がある」という句を理解できませんでした。

考慮する $f（x）：R \からR$

受け入れる $F（x）= f（x）$ 、つまり目的関数は与えられたものと一致します。

分解可能 $f（x）$ テイラー級数では、MHFとは異なり、2次近似が必要です。

$f（x + d）\約f（x）+ f ^ {'}（x）d + \ frac {1} {2} f ^ {' '}（x）d ^ 2、\ d \ in R ^ n、|| d || \ to 0 \タグ{4}$

それを示すのは簡単です $f {'}（x）\ ne 0$ 、関数は極値を持つことができません $x$ 。ポイント $x ^ * $ $ f {'}（x）= 0$ 定置と呼ばれる。

私たちは、に関して両側を区別します $d$ 。私たちの目標は $f（x + d）^ {'} = 0$ 、したがって、方程式を解きます。

$0 = f（x + d）^ {'} = f ^ {'}（x）+ f ^ {''}（x）d \\ d_ {n} =-\ frac {f ^ {'}（x ）} {f ^ {''}（x）}$

$d_n$ -これは極値の方向ですが、最大値と最小値の両方にすることができます。ポイントがあるかどうかを確認するには $x + d_n$ 最小-二次導関数を分析する必要があります。もし $f ^ {''}（x）＆gt; 0 $、次に$ f（x +d_）$ 極小値の場合 $f ^ {''}（x）＆lt; 0$ -最大。

多次元の場合、1次導関数は勾配に、2次導関数はヘッセ行列に置き換えられます。行列を分割することはできません。代わりに、逆数を掛けます（可換性がないため、側面を観察します）。

$f（x）：R ^ n \ to R \\ H（x）d_ {n} =-\ nabla f（x）\\ d_ {n} =-H ^ {-1}（x）\ nabla f（ x）$

1次元の場合と同様に、正しいかどうかを確認する必要がありますか？ヘッセ行列が正定値の場合、方向は正しいです。そうでない場合は、MHCを使用します。

コード内：

 def is_pos_def(x): return np.all(np.linalg.eigvals(x) > 0) class NewtonOptimizer(Optimizer): def next_point(self): hesse = self.hesse(self.x) # if Hessian matrix if positive - Ok, otherwise we are going in wrong direction, changing to gradient descent if is_pos_def(hesse): hesseInverse = np.linalg.inv(hesse) nextX = self.x - self.learningRate * np.dot(hesseInverse, self.gradient(self.x)) else: nextX = self.x - self.learningRate * self.gradient(self.x) return self.move_next(nextX)

結果：

反復	X	Y	Z
25	-1.49	0.63	4.36
75	0.31	-0.04	0.244
179	0.995	-0.991	$10 ^ {-6}$

MHCと比較してください。 25回の反復まで非常に強い下降がありました（ほぼ山から落ちました）が、その後収束は大幅に遅くなりました。ミネソタ州では、逆に、最初はゆっくりと山を下っていきますが、その後は速く動きます。 MNSは、25から532回の繰り返しでゼロに達しました。 $z = 0.334$ 。 MN最適化 $4.36$ 最後の154回の繰り返し。

これは一般的な動作です。ローカル極値に近いポイントから開始する場合、MNは2次収束率を持ちます。 MHCは極端からはほど遠いです。

MNは、上の図で見られた曲率の情報を使用します（丘からの滑らかな降下）。

このアイデアを示す別の例：下の図では、赤いベクトルはMNSの方向であり、緑はMNです

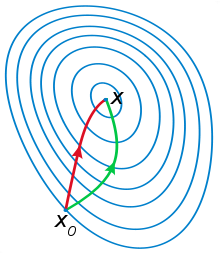
[非線形vs線形]最小二乗法

MNCには、モデルがあります $y = f（\ beta_1、.. \ beta_n; x）$ 持っている $n$ 最小化するように構成されたパラメーター

$\ frac {1} {2} \ sum \ limits_ {i = 1} ^ {N}（y_i'-y_i）^ 2 = \ frac {1} {2} \ sum \ limits_ {i = 1} ^ {N } r_i ^ 2$

どこで $y_i '$ - $私は$ 観察。

線形最小二乗法では、$ m $方程式があり、それぞれが線形方程式として表すことができます

$x_i \ beta_1 + x_i \ beta_2 + .. x_i \ beta_n = y_i$

線形最小二乗法のソリューションは一意です。行列方程式の1つの近似解で線形OLSの解を見つけることができるQR分解、 SVD分解などの強力な方法があります。 $Ax = b$ 。

非線形最小二乗パラメーター $\ beta_i$ たとえば、それ自体が関数で表される場合があります $\ beta_i ^ 2$ 。また、パラメータの積があるかもしれません、例えば

$\ beta_1 \ beta_2$

など

ここでは、解決策を繰り返し見つける必要があり、解決策は開始点の選択に依存します。

以下の方法は、非線形の場合を扱います。しかし、最初に、タスクのコンテキストで非シェディング最小二乗法を見てみましょう-関数を最小化

$f：R ^ 2 \ to R \\ F（x_1、x_2）= f（x_1、x_2）= \ frac {1} {2}（1-x_1）^ 2 + \ frac {1} {2}（x_2 -x_1 ^ 2）^ 2 = \ frac {1} {2} r_1 ^ 2（x_1、x_2）+ \ frac {1} {2} r_2 ^ 2（x_1、x_2）$

何にも似ていませんか？これはOLSの単なる形式です！ベクトル関数を導入します $r$

$r：R ^ 2 \ to R ^ 2 \\ r = \ left [\ begin {matrix} 1-x_1 \\ x_2-x_1 ^ 2 \ end {matrix} \ right]$

そして私たちは選択します $x_1、x_2$ 連立方程式を解くために（少なくともおよそ）：

$\ begin {cases} r_1 = 1-x_1 = 0 \\ r_2 = x_2-x_1 ^ 2 = 0 \ end {cases} \\$

次に、測定値が必要です。つまり、近似値はどれほど良いのでしょうか。ここにあります：

$F（x）= \ frac {1} {2} \ sum_i ^ m r_i ^ 2（x）= \ frac {1} {2} r ^ T r = \ frac {1} {2} || r || ^ 2 \タグ{5}$

逆演算を適用しました：ベクトル関数を微調整しました $r$ ターゲットの下 $F$ 。しかし、それは可能であり、その逆も同様です。ベクトル関数が与えられた場合 $r：R ^ n \からR ^ m$ 建物 $F（x）$ （5）から。例：

$r = \左[\ begin {matrix} x_1 ^ 2 \\ x_2 ^ 2 \ end {matrix} \ right]、F（x）= \ frac {1} {2} x_1 ^ 2 + \ frac {1} { 2} x_2 ^ 2$

最後に、非常に重要な瞬間。条件を満たす必要があります $m \ ge n$ それ以外の場合は、メソッドを使用できません。私たちの場合、条件は満たされています

ガウス・ニュートン法

この方法は同じ線形近似に基づいていますが、現在は2つの関数を扱っています。

$r（x + d）\約l（d）\ equiv r（x）+ J（x）d \\ F（x + d）\約L（d）\ equiv \ frac {1} {2} l ^ T（d）l（d）$

次に、ニュートン法と同じことを行います-方程式を解きます（ $L（d）$ ）：

$L ^ {''} d_ {zn} = -L ^ {'}$

近いことを示すのは簡単です $\テキスト（\ d \から0）$ ：

$L ^ {''}（d）= J_r ^ T J_r、\ L ^ {'}（d）= J_r ^ T（d）r（d）\\（J ^ TJ）d_ {mn} = -J ^ Tr \\ d_ {mn} =-（J ^ TJ）^ {-1} J ^ Tr$

オプティマイザーコード：

 class NewtonGaussOptimizer(Optimizer): def next_point(self): # Solve (J_t * J)d_ng = -J*f jacobi = self.jacobi(self.x) jacobisLeft = np.dot(jacobi.T, jacobi) jacobiLeftInverse = np.linalg.inv(jacobisLeft) jjj = np.dot(jacobiLeftInverse, jacobi.T) # (J_t * J)^-1 * J_t nextX = self.x - self.learningRate * np.dot(jjj, self.function_array(self.x)).reshape((-1)) return self.move_next(nextX)

結果は私の期待を超えました。わずか3回の繰り返しで、 $（x = 1、y = 1）$ 。軌道を示すために、 学習率を0.2に減らしました

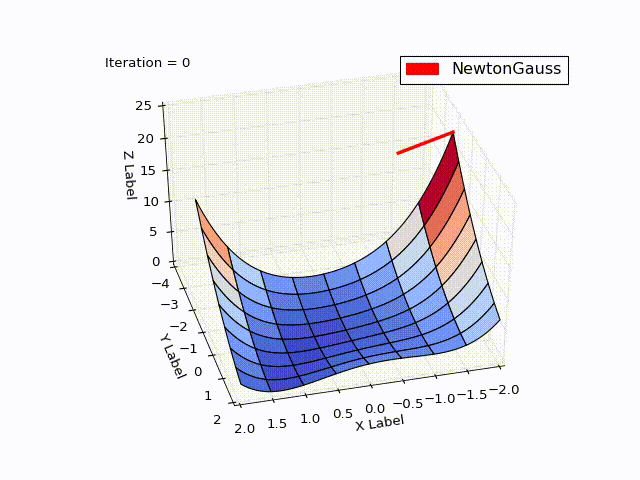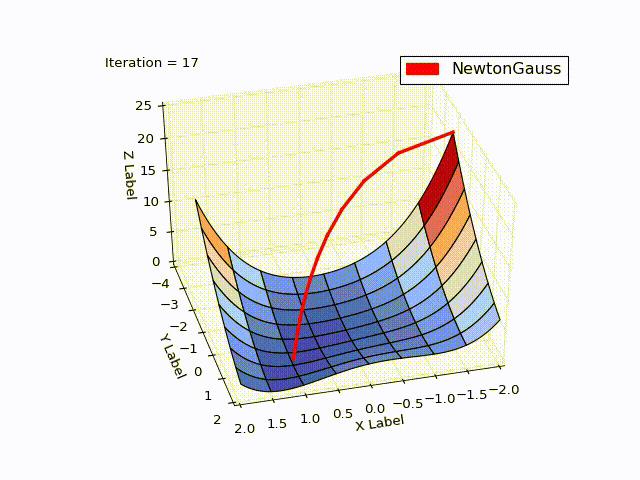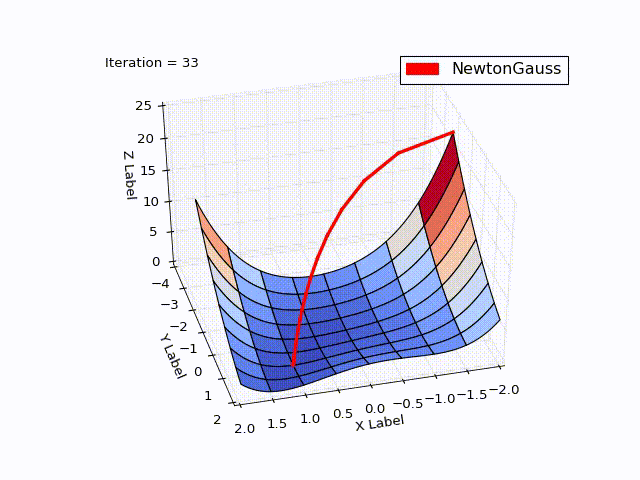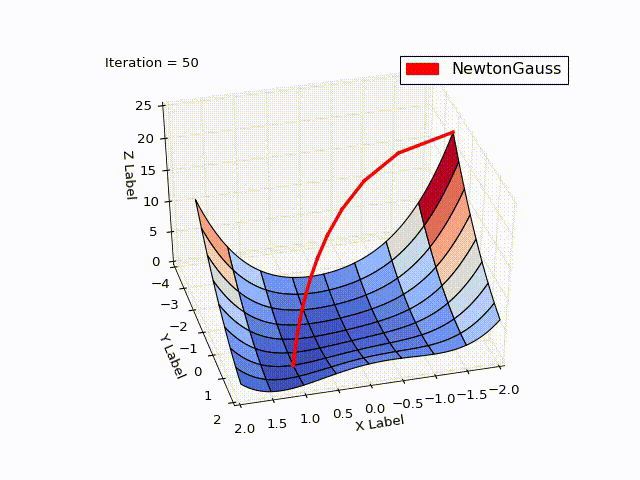
レーベンバーグ・マルカートアルゴリズム

これは、Gauss-Newton Methodのいずれかのバージョン（「 減衰バージョン 」）に基づいています。

$（J ^ T J + \ mu I）d_ {lm} = -J ^ Tr、\ mu \ ge 0$

$\ mu$ 規制パラメータと呼ばれます。時々 $私は$ に置き換えられました $diag（J ^ T J）$ 収束を改善します。

対角要素 $J ^ T J$ ポジティブになるから要素 $a_ {ii}$ 行列 $J ^ T J$ 行ベクトルのスカラー積です $私は$ で $J ^ t$ 自分で。

大規模 $\ mu$ それは小さなもののための最も急な降下の方法-ニュートン法が判明しました。

最適化プロセスのアルゴリズム自体が目的のものを選択します $\ mu$ 次のように定義されるゲイン比に基づきます。

$g = \ frac {F（x）-F（x_ {new）}} {L（0）-L（d_ {lm}）}$

もし $g＆gt; 0$ それから $L（d）$ -の良い近似 $F（x + d）$ そうでなければ、増やす必要があります $\ mu$ 。

初期値 $\ mu$ として与えられます $\ tau \ cdot max \ {{a_ {ij}} \}$ どこで $a_ {ij}$ -行列要素 $J ^ T J$ 。

$\タウ$ に推奨 $10 ^ {-3}$ 。停止基準は、グローバルな最小値を達成することです。 $F ^ {'}（x ^ *）= g（x ^ *）= 0$

オプティマイザーでは、停止基準を実装しませんでした-ユーザーがこれを担当します。次のポイントに移動するだけでした。

 class LevenbergMarquardtOptimizer(Optimizer): def __init__(self, function, initialPoint, gradient=None, jacobi=None, hessian=None, interval=None, function_array=None, learningRate=1): self.learningRate = learningRate functionNew = lambda x: np.array([function(x)]) super().__init__(functionNew, initialPoint, gradient, jacobi, hessian, interval, function_array=function_array) self.v = 2 self.alpha = 1e-3 self.m = self.alpha * np.max(self.getA(jacobi(initialPoint))) def getA(self, jacobi): return np.dot(jacobi.T, jacobi) def getF(self, d): function = self.function_array(d) return 0.5 * np.dot(function.T, function) def next_point(self): if self.y==0: # finished. Y can't be less than zero return self.x, self.y jacobi = self.jacobi(self.x) A = self.getA(jacobi) g = np.dot(jacobi.T, self.function_array(self.x)).reshape((-1, 1)) leftPartInverse = np.linalg.inv(A + self.m * np.eye(A.shape[0], A.shape[1])) d_lm = - np.dot(leftPartInverse, g) # moving direction x_new = self.x + self.learningRate * d_lm.reshape((-1)) # line search grain_numerator = (self.getF(self.x) - self.getF(x_new)) gain_divisor = 0.5* np.dot(d_lm.T, self.m*d_lm-g) + 1e-10 gain = grain_numerator / gain_divisor if gain > 0: # it's a good function approximation. self.move_next(x_new) # ok, step acceptable self.m = self.m * max(1 / 3, 1 - (2 * gain - 1) ** 3) self.v = 2 else: self.m *= self.v self.v *= 2 return self.x, self.y

結果も良好です。

反復	X	Y	Z
0	-2	-2	22.5
4	0.999	0.998	$10 ^ {-7}$
11	1	1	0

learningrate = 0.2の場合：

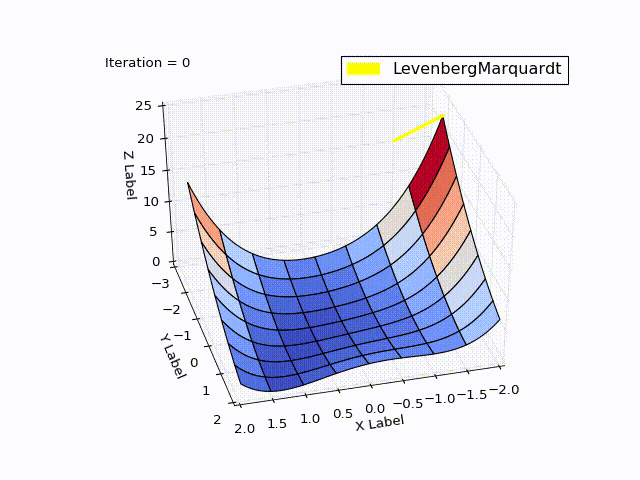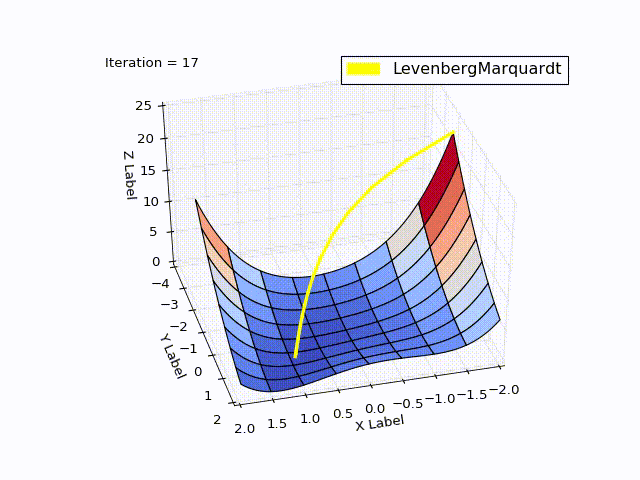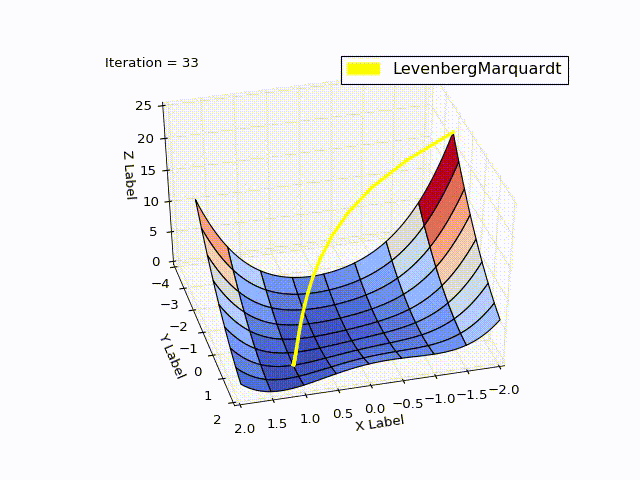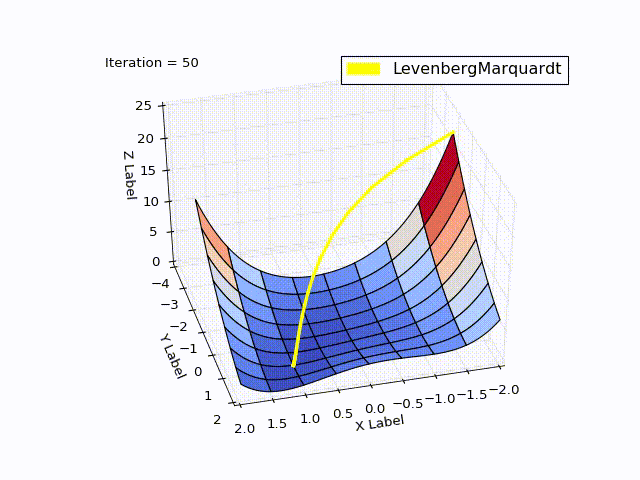
メソッド比較

メソッド名	対象機能	長所	短所	収束
最急降下法	微分可能	-幅広いアプリケーション簡単な実装 -1回の反復で低コスト	-グローバル最小値は他の方法よりも悪く見える -極値近くの低い収束率	ローカル
ニュートンの方法	二度微分可能	-極値付近の高い収束率 -曲率情報を使用します	-関数は2回微分可能でなければなりません -ヘッセ行列が縮退している場合（逆行列がない場合）、エラーを返します -それが極端からかけ離れている場合、間違ってしまう可能性があります	ローカル
ガウス・ニュートン法	非線形最小二乗	-非常に高い収束率 -カーブフィッティングタスクとうまく機能します	-行列Jの列は線形独立でなければならない -目的関数のタイプに制限を課す	ローカル
レーベンバーグ・マルカートアルゴリズム	非線形最小二乗	-考慮された方法の中で赤ちゃんの安定性 -グローバルな極値を見つける最大のチャンス -非常に高い収束率（適応） -カーブフィッティングタスクとうまく機能します	-行列Jの列は線形独立でなければならない -目的関数のタイプに制限を課す -実装の複雑さ	ローカル

特定の例では良好な結果が得られていますが、検討した方法ではグローバル収束を保証していません（これは見つけるのが非常に難しいタスクです）。それにもかかわらず、これを達成できる少数の方法の例は、流域ホッピングアルゴリズムです。

結合された結果（特に最後の2つの方法の速度が低下しました）：

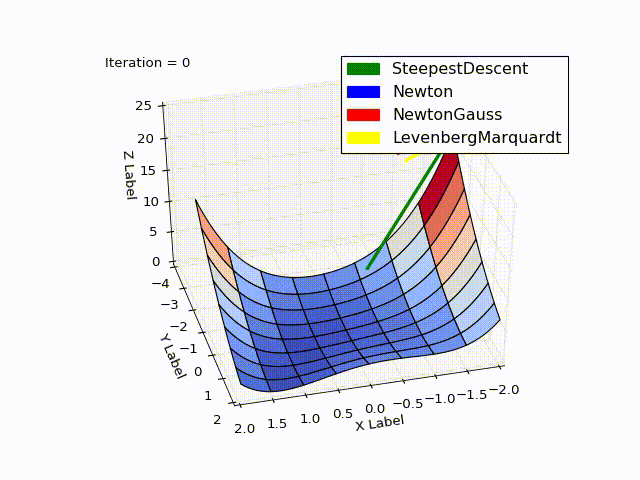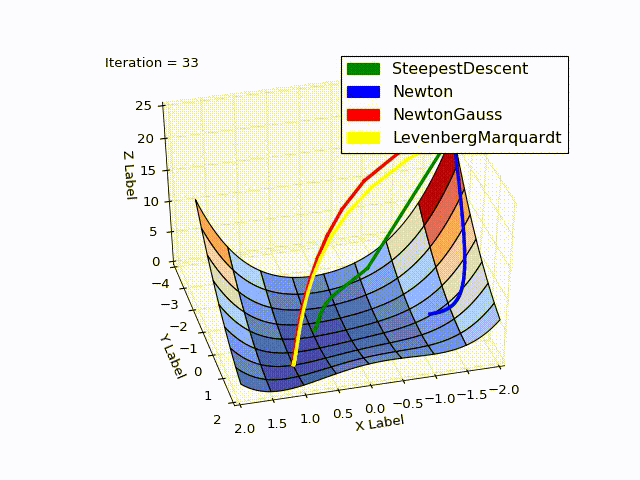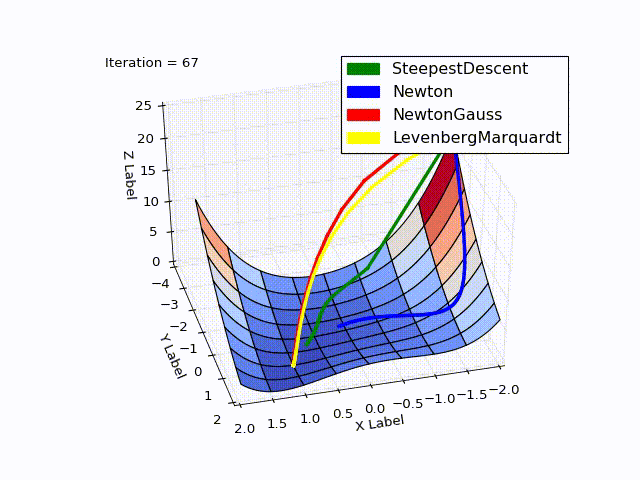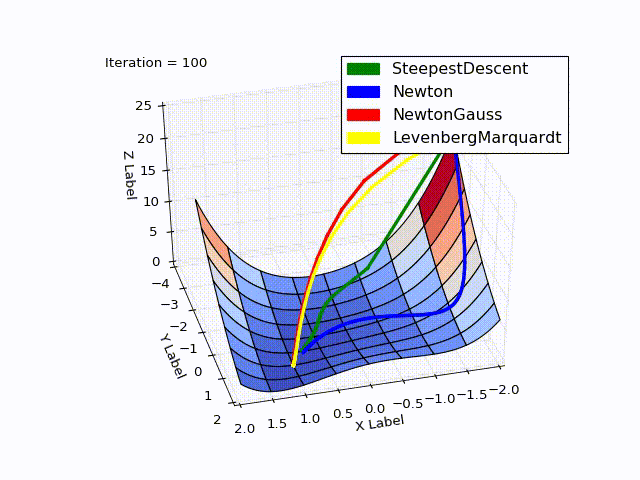
ソース はgithubからダウンロードできます

ソース

K.マドセン、HBニールセン、O。ティンレフ（2004）：非線形最小二乗法
Florent Brunet（2011）：継続的最適化の基礎
最小二乗問題

Levenberg-非線形最小二乗法のMarquardtアルゴリズムとPythonでの実装

More articles: