最初にいくつかの紹介的な言葉があります。 外部クロッキングなしで、任意の回路を非同期で呼び出すことができます。 さらに、異なる種類の非同期回路は異なる動作原理を使用し、自己同期回路はその種類の1つにすぎません。 自己同期の下では、通常、いわゆるを理解します。 半モジュラースキームは、半モジュラーラティスを構成する代数構造の形式で表現する可能性があるためです(可能性のある不正確さについては数学者を許してください)。 セミモジュラー(読み取り-自己同期)回路の機能の1つは、遅延に依存しないことです。これは、実際には、トランジスタがスイッチング可能な任意の条件下で回路が動作可能であることを意味します。 ただし、機械式リレーまたはその他のスイッチで自己同期回路を設計する必要はありません。 このようなスキームの開発が非常に困難であることは秘密ではありませんが、たとえば過熱や老化の影響による障害で脅かされることはありません。
すべてを導入すると、練習に進むことができます。 設計方法により、すべての自己同期回路は、制御オートマトンと多くのロジックを持つ回路の2つのグループに分けることができます。 この分離はどこから来たのですか? 自動コントローラーは、カウンター、ラッチ、トリガー、またはいくつかの小さなコントローラーのような単純なデバイスです。 これらのデバイスは、主にペトリネット(並列動的プロセスを記述するためのグラフ言語)を使用して手動で設計され、その後Petrifyまたは他のツールで合成されます。 多くのロジックを備えた回路は、周辺機器コントローラ、DAP、演算ユニット、および乗算、加算、比較、多重化などを使用するその他すべてのコンピューティングデバイスのすべてのノードに精通していると理解する必要があります。 このようなスキームは、ペトリネットで説明するのが難しすぎて、異なって設計されています(これは、出版物の別個のサイクル、または教科書全体のトピックです)。 したがって、基本から始め、ペトリネットから始めます。
最も簡単な自己同期カウントトリガーを例として取り上げます。 すべての自己同期回路と同様に、インバーターのリングジェネレーターと同じ原理で動作します。
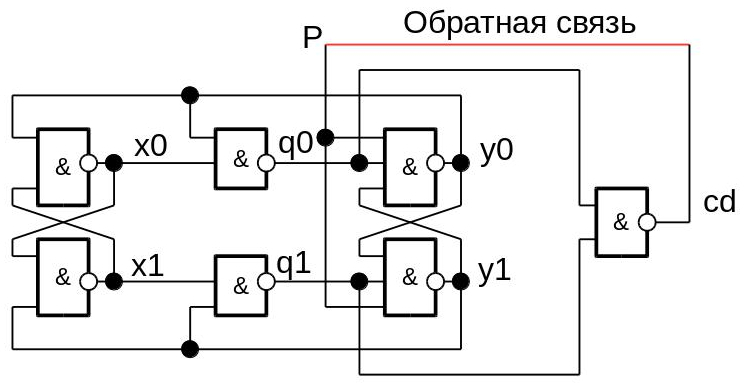
信号Pはカウント可能で、信号x0、x1、y0、y1は内部、{ q0、q1 }のペアはカウンタの出力信号、 cdは回路内の過渡現象の終了のインジケータです。 信号cdがカウント入力Pに短絡すると、マシンは無期限に動作します。 ご希望の方は、おなじみのモデリングの助けを借りてこれを確信することができます:
テストベンチを使用したネットリストソースコード
`timescale 1ns/10ps module sim(); wire P,cd; counter dut(.P(P), .cd(cd)); assign P = cd; initial begin force P=0; force dut.x0=0; force dut.x1=1; #2; release P; release dut.x1; release dut.x0; end endmodule module counter( input wire P, output wire cd ); wire x0, x1, y0, y1, q0, q1; nand2 U1 (.A(y0), .B(x1), .Y(x0)); nand2 U2 (.A(y1), .B(x0), .Y(x1)); nand2 U3 (.A(y0), .B(x0), .Y(q0)); nand2 U4 (.A(y1), .B(x1), .Y(q1)); nand3 U5 (.A(P), .B(q0), .C(y1), .Y(y0)); nand3 U6 (.A(P), .B(q1), .C(y0), .Y(y1)); nand2 U7 (.A(q0), .B(q1), .Y(cd)); endmodule module nand2( input wire A, B, output wire Y ); assign #1 Y = ~(A & B); endmodule module nand3( input wire A, B, C, output wire Y ); assign #1 Y = ~(A & B & C); endmodule
論理要素にはゼロ以外の遅延が必要であり、回路には初期インストールが必要であることに注意してください。 鉄の場合(誰かがこのスキームをFPGAまたはプレーサーで作成しようとする場合)、初期インストールは必要ありません。
次に、リバースエンジニアリングを行って、ペトリネットを使用してカウントトリガー回路を取得する方法を見つけましょう。 要素の出力で値の任意の初期配置を選択します(シミュレーションから取得することも、自分で作成することもできます)。
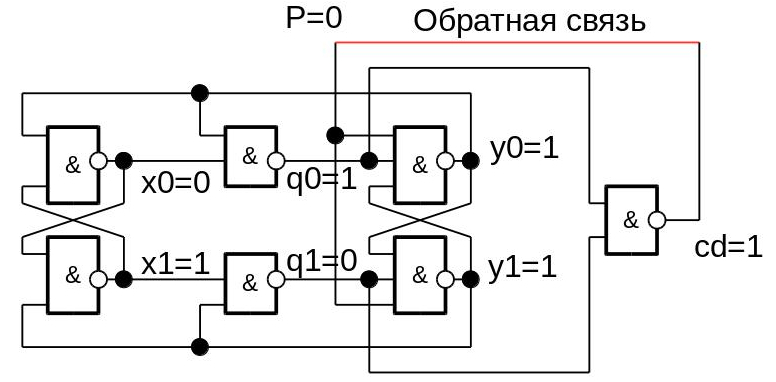
P = cdであるため、 Pの値は次の瞬間に1だけ変化するはずです変数のエッジと変数の切り替えの方向があるエッジにグラフを作成します。 変数を0から1に切り替えた場合は+記号でマークし、1から0に切り替えた場合はマイナス記号でマークします。Workcraftエディターにグラフを入力します( http://www.workcraft.orgから無料でダウンロードできます。[ファイル]メニューを選択します-作業の作成-信号遷移グラフ、およびグラフを入力します)。 信号Pの 0から1への最初の切り替え(つまり、P +)は、円(トークン)の入った矢印でマークされています。 グラフは次のようになります。
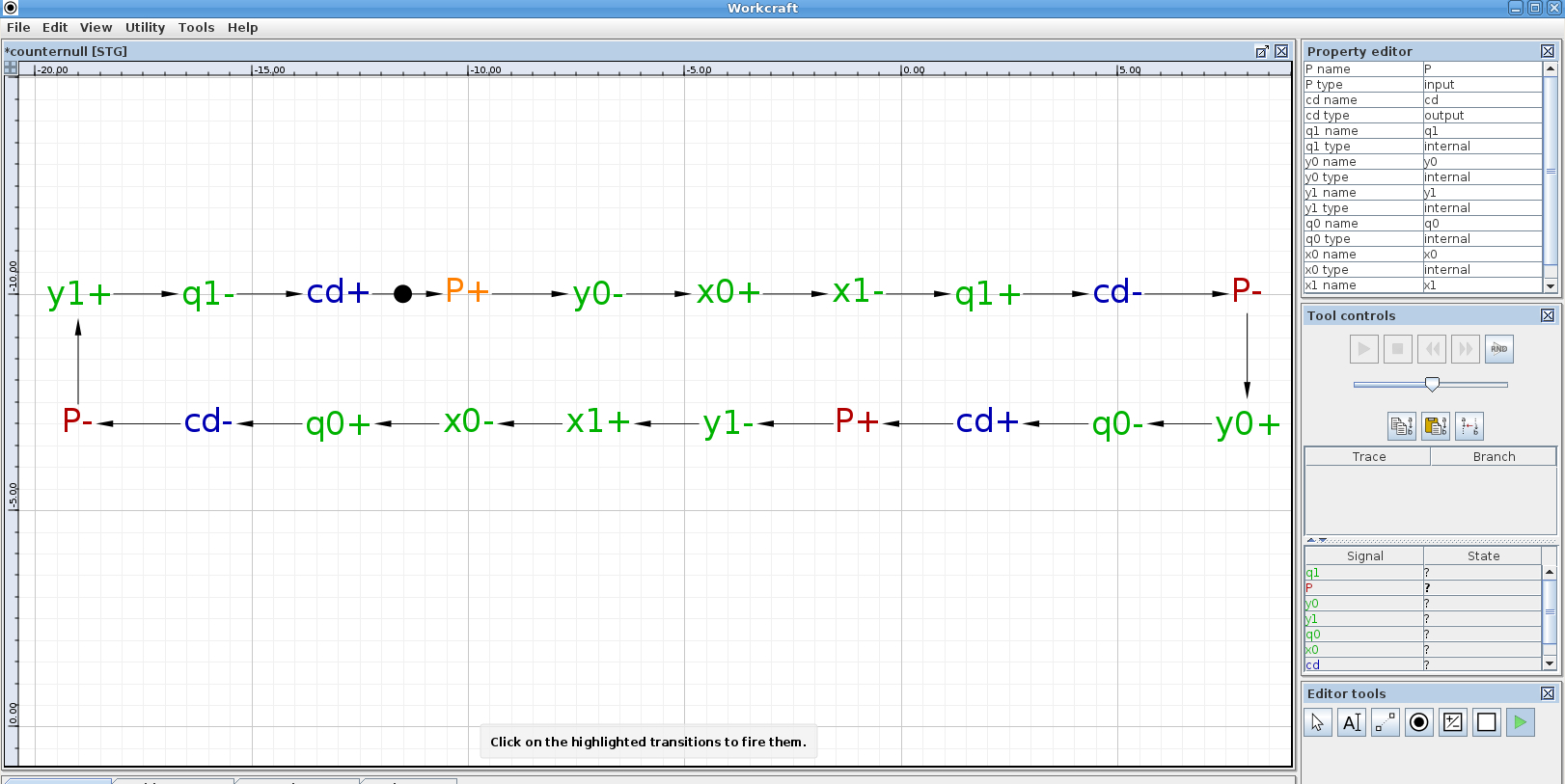
Pを1に切り替えた後、最初に戻るまで、信号y0は0に、次にx0は1に、などに切り替わります。 グラフからわかるように、出力変数{ q1、q0 }はサイクル10-11-01-11-10-11などで切り替えられます。これは、カウントトリガーの動作に対応します。 エディターツールの右下のウィンドウにある緑色の三角形のアイコンをクリックしてペトリネット操作のシミュレーターを有効にし、上に表示される[ツールコントロール]ウィンドウでシミュレーションを実行できます。
次のステップは、Petrifyでのグラフ合成です。 メニューからツール-合成-複雑なゲート合成[Petrify]を選択し、ログを取得します。
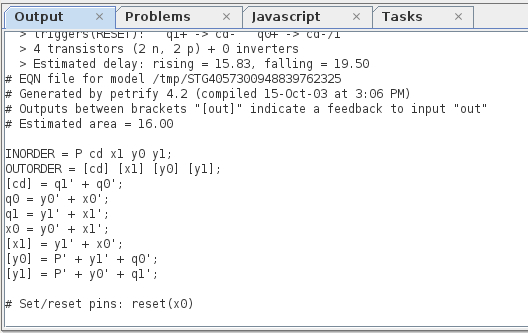
合成は成功し(これは、回路が
グラフから、カウントトリガーのパフォーマンスは遅延に依存しないことが明らかになります:回路内のどこで遅延を追加しても、動作が遅くなるだけで、スイッチング要素の順序は変更されず、回路のロジックに違反しません。
説明された手順(順序:グラフから回路)では、50個以下の変数を含むペトリネットによって動作が記述されるラッチ、トリガー、カウンター、または任意のコントローラーのみの自己同期の合成とチェックが可能です。 この方法では、より複雑なスキームを開発することはできません(他の設計アプローチを使用する必要があります)。 しかし、自己同期回路の開発の基本を学ぶために、考慮されるカウントトリガーの例(およびワーククラフト配布キットのチュートリアル)はまさにそれです。 理論に興味のある人には、ペトリネットと自己同期回路に関する教科書を読むことをお勧めします。MarakhovskyV. B.、Rosenblum L. Ya。、Yakovlev A. V.並列プロセスのモデリング。 ペトリネット 、およびワーククラフト開発者向けサイトの学習資料。