主成分分析（PCA）が簡単な例でどのように機能するか

この記事では、数学装置の背後にある直感の観点から、主成分分析（PCA）メソッドがどのように機能するかについてお話したいと思います。 できるだけシンプルですが、詳細に。



数学は一般に非常に美しくエレガントな科学ですが、その美しさは多くの抽象化層の背後に隠れている場合があります。 結局のところ、すべてが一見したように見えるよりもはるかに簡単であることが判明しているため、最も重要なことは理解して想像することです。



他の分析と同様に、データ分析では、状況をできる限り正確に記述する単純化されたモデルを作成すると役立つ場合があります。 多くの場合、兆候は相互に大きく依存しており、それらの同時存在は冗長です。



たとえば、当社の燃料消費量は100キロメートルあたりのリットルで測定され、米国ではガロンあたりのマイルで測定されます。 一見、値は異なりますが、実際には互いに厳密に依存しています。 マイル1600m、ガロン3.8l。 1つの兆候は厳密に他の兆候に依存します。



しかし、はるかに頻繁に、サインがそれほど厳密ではなく、互いに依存していることが起こります（これは重要です！）明示的ではありません。 エンジン全体の体積は、100 km / hまでの加速にプラスの影響を与えますが、これは常に正しいとは限りません。 そして、一見すると見えない要因（燃料の品質の改善、より軽い材料の使用やその他の近代的な成果など）を考慮すると、自動車の年は強くないことがわかりますが、それは加速にも影響します。



依存関係とその強さを知っているので、いくつかの機能を1つで表現し、いわば統合して、より単純なモデルで作業できます。 もちろん、情報の損失を回避することは不可能である可能性が最も高くなりますが、PCAメソッドだけでそれを最小限に抑えることができます。



より厳密に表現すると、この方法は観測値のn次元クラウドを楕円体（n次元）に近似し、その半軸が将来の主要コンポーネントになります。 そして、そのような軸に投影するとき（次元削減）、最大量の情報が保存されます。

ステップ1.データの準備

ここでは、例を簡単にするために、数十個の兆候と数百個の観察のための実際のトレーニングデータセットは使用しませんが、できるだけ単純なおもちゃの例を作成します。 2つの兆候と10の観察結果は、アルゴリズムの腸で何が、そして最も重要なのはなぜ起こるのかを説明するのに十分です。



サンプルを生成します。

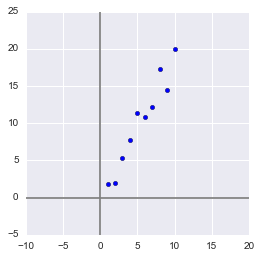
x = np.arange(1,11) y = 2 * x + np.random.randn(10)*2 X = np.vstack((x,y)) print X OUT: [[ 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. ] [ 2.73446908 4.35122722 7.21132988 11.24872601 9.58103444 12.09865079 13.78706794 13.85301221 15.29003911 18.0998018 ]]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

このサンプルでは、​​互いに強く相関する2つの機能があります。 PCAアルゴリズムを使用すると、機能の組み合わせを簡単に見つけることができ、情報を犠牲にしてこれらの機能の両方を1つの新しい機能で表現できます。 それでは正しくやってみましょう！



まず、いくつかの統計。 モーメントはランダム変数を記述するために使用されることを思い出してください。 マットが必要です。 期待と分散。 そのマットと言えます。 期待は大きさの「重心」であり、分散はその「サイズ」です。 大まかに言えば、マット。 期待値はランダム変数の位置を設定し、分散はそのサイズ（より正確にはスプレッド）を決定します。



情報の損失を最小限に抑えるために、ベクトルはサンプルの中心を通過する必要があるため、ベクトルに投影するプロセスは平均値に影響しません。 したがって、サンプルを中央に配置しても構いません-属性の平均値が0になるようにサンプルを線形にシフトします。これにより、以降の計算が大幅に簡素化されます（中央に配置しなくても実行できることに注意してください）。

シフト演算子の逆は、初期平均値のベクトルに等しくなります-サンプルを元の次元に復元する必要があります。

 Xcentered = (X[0] - x.mean(), X[1] - y.mean()) m = (x.mean(), y.mean()) print Xcentered print "Mean vector: ", m OUT: (array([-4.5, -3.5, -2.5, -1.5, -0.5, 0.5, 1.5, 2.5, 3.5, 4.5]), array([-8.44644233, -8.32845585, -4.93314426, -2.56723136, 1.01013247, 0.58413394, 1.86599939, 7.00558491, 4.21440647, 9.59501658])) Mean vector: (5.5, 10.314393916)
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

一方、分散は、ランダム変数の値の順序に強く依存します。 スケーリングに敏感。 したがって、フィーチャの測定単位の順序が大幅に異なる場合は、それらを標準化することを強くお勧めします。 この場合、値の順序はそれほど変わらないので、例を簡単にするために、この操作は実行しません。

ステップ2.共分散行列

多次元ランダム変数（ランダムベクトル）の場合、中心の位置はまだ合致します。 軸上の予測の期待。 しかし、その形状を説明するには、軸に沿った分散だけでは十分ではありません。 これらのグラフを見てください。3つのランダム変数はすべて同じ期待値と分散を持ち、軸上での全体の投影は同じです。







ランダムベクトルの形状を記述するには、共分散行列が必要です。



これは、 （i、j）要素が特徴（X _i 、X _j ）の相関である行列です。 共分散の式を思い出してください。











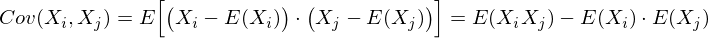
私たちの場合、 E（X _i ）= E（X _j ）= 0なので 、単純化されます：











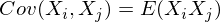
X _i = X _jの場合 ：











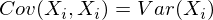
これは、任意のランダム変数に当てはまります。



したがって、対角線上のマトリックスでは属性の分散があり（i = jであるため）、残りのセルでは対応する属性のペアの共分散があります。 また、共分散の対称性により、行列も対称になります。

注：共分散行列は、多次元ランダム変数の場合の分散の一般化です-分散だけでなく、ランダム変数の形状（スプレッド）も記述します。

実際、1次元確率変数の分散は1x1共分散行列であり、その唯一の項は式Cov（X、X）= Var（X）で与えられます。



したがって、サンプルの共分散行列Σを作成します。 これを行うために、分散X _iおよびX _jとそれらの共分散を計算します。 上記の式を使用できますが、Pythonを使用しているため、 numpy.cov（X）関数を使用しないのは罪です。 入力として、ランダム変数のすべての属性のリストを受け取り、その共分散行列を返します。ここで、Xはn次元のランダムベクトル（n行の数）です。 この関数は、不偏分散の計算、2つの量の共分散、および共分散行列のコンパイルに優れています。

（Pythonでは、行列は行配列の列配列として表されることを思い出してください。）

 covmat = np.cov(Xcentered) print covmat, "\n" print "Variance of X: ", np.cov(Xcentered)[0,0] print "Variance of Y: ", np.cov(Xcentered)[1,1] print "Covariance X and Y: ", np.cov(Xcentered)[0,1] OUT: [[ 9.16666667 17.93002811] [ 17.93002811 37.26438587]] Variance of X: 9.16666666667 Variance of Y: 37.2643858743 Covariance X and Y: 17.9300281124
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ステップ3.固有ベクトルと値（固有ペア）

さて、ランダム変数の形状を説明するマトリックスが得られ、そこからxとy（つまりX ₁とX ₂ ）の次元と、平面上の近似形状を取得できます。 次に、サンプルの投影のサイズ（分散）が最大になるようなベクトル（この場合は1つのみ）を見つける必要があります。

注：分散の高次元への一般化は共分散行列であり、これら2つの概念は同等です。 ベクトルに投影する場合、投影の分散は最大化され、大きな次数の空間に投影する場合、その共分散行列全体が最大化されます。

したがって、ランダムベクトルXを投影する単位ベクトルを取得します。その後、その投影はv ^T Xに等しくなります。ベクトルへの投影の分散は、Var（v ^T X）になります。 一般的な形式では、ベクトル形式（中心量の場合）では、分散は次のように表されます。











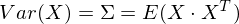
したがって、投影の分散：











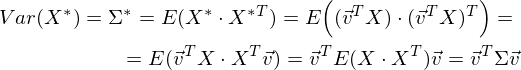
分散が最大値v TΣvで最大化されることは簡単にわかります。 ここでレイリーの態度は私たちを助けます。 数学に深く入り込むことなく、レイリー関係には共分散行列の特別なケースがあるとだけ言います。









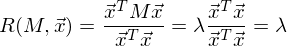
そして









最後の式は、行列を固有ベクトルと値に分解するトピックに精通している必要があります。 xは固有ベクトルであり、λは固有値です。 固有ベクトルと値の数は、行列のサイズに等しくなります（値は繰り返すことができます）。

ところで、英語では、固有値とベクトルはそれぞれ固有値と固有ベクトルと呼ばれます。

それは私たちの言葉よりもはるかに美しく（そして簡潔に）聞こえるように思えます。

したがって、投影の最大分散の方向は常に固有ベクトルと一致し、固有ベクトルはこの分散の値に等しくなります 。



これは、より多くの次元への投影にも当てはまります。m次元空間への投影の分散（共分散行列）は、最大固有値を持つm個の固有ベクトルの方向で最大になります。



サンプルの次元は2で、その中の固有ベクトルの数はそれぞれ2です。それらを見つけます。



numpyライブラリは、関数numpy.linalg.eig（X）を実装します。Xは正方行列です。 固有値の配列と固有ベクトルの配列（列ベクトル）の2つの配列を返します。 そして、ベクトルは正規化されます-それらの長さは1です。必要なものだけです。 これらの2つのベクトルは、サンプルの新しい基底を定義し、その軸がサンプルの近似楕円の半軸と一致するようにします。





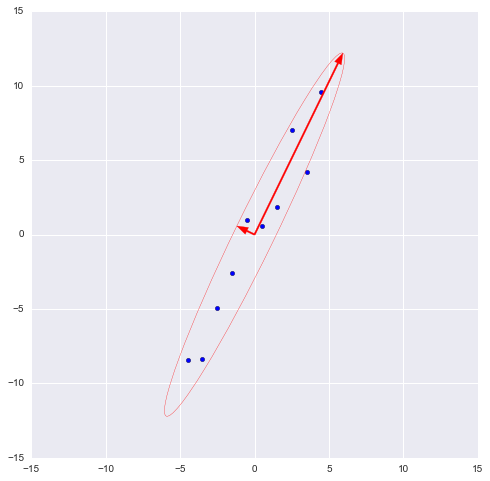
このグラフでは、サンプルを半径2シグマの楕円で近似しました（つまり、すべての観測値の95％を含むはずです-原則としてここで観測します）。 大きなベクトルを反転しました（eig（X）関数はそれを反対方向に向けました）-ベクトルの向きではなく方向が重要です。

ステップ4.次元削減（投影）

最大のベクトルの方向は回帰直線に似ており、サンプルを投影すると、回帰の残りの項の合計に相当する情報が失われます（Yのデルタではなく、距離のみがユークリッドになります）。 私たちの場合、サイン間の関係は非常に強いため、情報の損失は最小限に抑えられます。 前のグラフからわかるように、投影の「価格」-小さい固有ベクトルの分散-は非常に小さいです。

注：共分散行列の対角要素は元の基底に沿った分散を示し、その固有値は新しい基底に従って（主成分とともに）分散を示します。

多くの場合、失われた（および保存された）情報の量を見積もる必要があります。 パーセンテージで表示するのが最も便利です。 各軸に沿った分散を取得し、軸に沿った分散の合計（つまり、共分散行列のすべての固有値の合計）で除算します。

したがって、大きいベクトルは45.994 / 46.431 * 100％= 99.06％を表し、小さいベクトルはそれぞれ約0.94％です。 小さいベクトルを破棄し、大きいベクトルにデータを投影すると、情報の1％未満しか失われません。 素晴らしい結果です！

注：実際には、ほとんどの場合、情報の合計損失が10〜20％を超えない場合、ディメンションを安全に削減できます。

投影を実行するには、ステップ3で前述したように、演算v ^T Xを実行する必要があります（ベクトルの長さは1でなければなりません）。 または、1つのベクトルではなく超平面がある場合、ベクトルv ^Tの代わりに基底ベクトルV ^Tの行列を使用します^。 結果のベクトル（または行列）は、観測の投影の配列になります。

 _, vecs = np.linalg.eig(covmat) v = -vecs[:,1]) Xnew = dot(v,Xcentered) print Xnew OUT: [ -9.56404107 -9.02021624 -5.52974822 -2.96481262 0.68933859 0.74406645 2.33433492 7.39307974 5.3212742 10.59672425]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

ドット（X、Y）は積です（したがって、Pythonでベクトルと行列を乗算します）



投影値が前のグラフの画像に対応していることは簡単にわかります。

ステップ5.データ復旧

プロジェクションを使用して作業し、それに基づいて仮説を立て、モデルを開発すると便利です。 しかし、常に受け取ったわけではないが、主要なコンポーネントには、部外者にとって明確で理解可能な意味があります。 たとえば、検出された異常値をデコードして、その背後にある観測値を確認すると便利な場合があります。



とても簡単です。 すべての必要な情報、つまり元の基底の基底ベクトルの座標（投影したベクトル）と平均のベクトル（センタリングをキャンセルする）があります。 たとえば、最大値である10.596 ...をデコードします。 これを行うには、右側に転置ベクトルを掛けて、平均のベクトルを追加するか、サンプル全体の一般的な形式で次のようにします。X ^T v ^T + m

 n = 9 #    Xrestored = dot(Xnew[n],v) + m print 'Restored: ', Xrestored print 'Original: ', X[:,n] OUT: Restored: [ 10.13864361 19.84190935] Original: [ 10. 19.9094105]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

違いは小さいですが、違いはあります。 結局、失われた情報は復元されません。 それでも、精度よりも単純さが重要な場合、復元された値は元の値に完全に近似します。

結論の代わりに-アルゴリズムのチェック

そのため、アルゴリズムを分解し、おもちゃの例でどのように機能するかを示しましたが、それを使用するため、sklearnに実装されたPCAと比較するだけです。

 from sklearn.decomposition import PCA pca = PCA(n_components = 1) XPCAreduced = pca.fit_transform(transpose(X))
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

n_componentsパラメーターは、投影が実行される次元の数、つまりデータセットを削減する次元の数を示します。 つまり、これらは最大の固有値を持つn個の固有ベクトルです。 次元を縮小した結果を確認します。

 print 'Our reduced X: \n', Xnew print 'Sklearn reduced X: \n', XPCAreduced OUT: Our reduced X: [ -9.56404106 -9.02021625 -5.52974822 -2.96481262 0.68933859 0.74406645 2.33433492 7.39307974 5.3212742 10.59672425] Sklearn reduced X: [[ -9.56404106] [ -9.02021625] [ -5.52974822] [ -2.96481262] [ 0.68933859] [ 0.74406645] [ 2.33433492] [ 7.39307974] [ 5.3212742 ] [ 10.59672425]]
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

sklearnのPCAは垂直配列を返しますが、結果は観測列ベクトルの行列として返されます（これは線形代数の観点からより標準的なビューです）。



原則として、これは重要ではありません。線形代数では列ベクトルを介して行列を記述することは標準的であり、データ（およびデータベースに関連する他の領域）の分析では、観測（トランザクション、レコード）は通常行に書き込まれることに注意してください。



他のモデルパラメーターもチェックしましょう-関数には、中間変数へのアクセスを許可するいくつかの属性があります。



-ベクトルの意味： mean_

-投影ベクトル（行列）： components_

-投影軸の分散（オプション）： explain_variance_

-情報の共有（合計分散の共有）： explain_variance_ratio_

注： explain_variance_はサンプル分散を示し、cov（）関数は不偏分散を計算して共分散行列を作成します！

取得した値をライブラリ関数の値と比較します。

 print 'Mean vector: ', pca.mean_, m print 'Projection: ', pca.components_, v print 'Explained variance ratio: ', pca.explained_variance_ratio_, l[1]/sum(l) OUT: Mean vector: [ 5.5 10.31439392] (5.5, 10.314393916) Projection: [[ 0.43774316 0.89910006]] (0.43774316434772387, 0.89910006232167594) Explained variance: [ 41.39455058] 45.9939450918 Explained variance ratio: [ 0.99058588] 0.990585881238
      
      

        
        
        
      

    
        
        
        
      
      

        
        
        
      

    
     

唯一の違いは分散にありますが、すでに説明したように、cov（）関数を使用しました。この関数は、不偏分散を使用しますが、explained_variance_属性は選択的なものを返します。 それらは、最初のものがマットを得るために（n-1）で割るという点と、2番目がnで割るという点でのみ異なります。 45.99∙（10-1）/ 10 = 41.39であることを確認するのは簡単です。



他のすべての値は同じです。つまり、アルゴリズムは同等です。 最後に、ライブラリアルゴリズムの属性はおそらく速度が最適化されているか、利便性のために単純に値を丸めているため（または何らかの不具合があるため）、ライブラリアルゴリズムの属性の精度が低いことに注意してください。

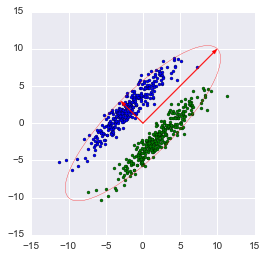
注：ライブラリメソッドは、分散を最大化する軸に自動的に投影します。 これは常に合理的ではありません。 たとえば、この図では、ディメンションのずさんな減少により、分類が不可能になります。 ただし、より小さいベクトルに投影すると、次元が正常に縮小され、分類子が保持されます。

そこで、PCAアルゴリズムの原理とsklearnでの実装を検証しました。 この記事が、データ分析に精通し始めたばかりの人には十分に理解でき、このアルゴリズムをよく知っている人には少なくとも少し有益であることを願っています。 直感的な表示は、メソッドの仕組みを理解するのに非常に役立ち、選択したモデルを適切に構成するには理解が非常に重要です。 ご清聴ありがとうございました！



PS：間違いの可能性について著者をauthorらないでください。 著者自身がデータ分析に精通している過程にあり、この驚くべき知識の分野を習得する過程で彼のような人々を助けたいです！ しかし、建設的な批判と多様な経験はあらゆる面で歓迎されています！