無線工学における検出問題の解決における統計的基準の適用

注釈

この記事では、統計的信号処理の基本と、ノイズを背景に最適な処理を行う方法について説明します。

はじめに

無線工学の主なタスクは、キャリアとして無線信号を使用した情報の受信、送信、および処理です。 無線システムの主な要件は、ソースから消費者にタイムリーで信頼できる情報を受信することです。 しかし、これはトランシーバーと信号伝搬媒体の動作原理の物理学によって妨げられます。その本質は、システムの物理パラメーターの変動と、確率的プロセスに関連するノイズ成分を持つ受信信号のランダム値です。



現時点では、有用な信号をノイズと干渉から区別する最も効果的な方法は最適な処理であり、通常は受信した入力の実装を有用な信号の既知の形状と比較することで実装されます。 さらに、その性質により弱く相関しているノイズは、この比較の程度を示す値への寄与が小さく、相関係数と呼ばれます。 したがって、検出タスクは少なくとも2つの仮説をテストすることになります。 一般的な場合、検出問題は2つの仮説で構成されます。H_0-受信デバイスの入力に信号がありません。H_1-受信デバイスの入力に信号があります。 検出アルゴリズムが異なると、他のさまざまな統計パラメーターでP {d_1 / H_1}を正しく検出する確率が異なります。 検出アルゴリズムの有効性を比較するための基準があり、確率的な量が処理されるため、これらの基準の性質は統計的です。 つまり、基準は比較の尺度として定義できます。

統計的検出基準

レーダーターゲットを検出するためのほとんどのアルゴリズムには、次の手順が含まれます。

1. 入力実装を受信する
2. 事前情報または事後情報に基づくしきい値の形成。
3. 入力実装の最適なフィルタリング
4. シグナル/ターゲットの存在を決定する

さらに、入力実装の受信としきい値の形成のシーケンスは、アルゴリズムのタイプに直接依存します。 受け入れられた入力実装に関する事後情報に基づいてしきい値を形成するアルゴリズムは、適応型と呼ばれます[1]。 基準は、タスクのタイプに基づいて経験的に選択されます。 たとえば、職場を選択する場合、通常、次の2つの基準が考慮されます。

• 稼いだお金と消費した電力の最大比率。
• 仕事から最大の喜び。

残念ながら、現代の現実はそのような専門家に優先順位をつけており、その専門家は彼のスキルによって製品をできるだけ早くリリースし、会社の利益を最大化することができます。 多くの場合、2番目の基準は破棄されるか、状況を分析するときに低い優先度が割り当てられます。 この場合、基準の優先順位を決定するインジケーターは、その力と呼ばれます。



数学的統計では、基準の力は、決定を行う際に第2種の間違いを犯さない確率として定義されます。 私たちの場合、第2種の間違い-これはそれ自体に最適なジョブには機能しません。一般的な場合、これは仮説H_0に対応するイベントの真理に対する誤った仮定です。



もちろん、普遍的な基準は存在しません。 したがって、たとえば、ある問題を解決するのに、別の問題を解決するのに最大の力を持つ基準は、この指標では最悪かもしれません。

最小リスク基準（ベイズ基準）

図1 Wの存在（U | A = 1）とWの非存在（U | A = 0）の条件付き確率密度の分布とエラー確率のグラフ



A = 1が信号s（t）の存在に対応し、A = 0がその不在に対応するとします。 解の集合dは、d_0→A = 1とd_1→A = 0の2つに縮退します。

バイナリ検出問題を解くとき、タスクはA = 1である仮説H_1とA = 0である対立仮説H_0をテストすることと同等であり、損失関数は正方行列になります。







したがって、A = 0での条件付きリスクはr_0 = C_00 P {d_0 / H_0} + C_01 P {d_1 / H_0} = C_00（1-P {d_1 / H_0}）+ C_01 P {d_1 / H_0}であり、 A = 1はr_1 = C_10 P {d_0 / H_1} + C_11 P {d_1 / H_1} = C_10（1-P {d_1 / H_1}）+ C_11 P {d_1 / H_1}と等しい、ここでP {d_1 / H_1}-正しく検出される確率、およびP {d_1 / H_0}-誤報の確率。



平均リスクはr̅= qr_0 + pr_1として定義されます。ここで、qは信号が存在しない事前確率、pは信号が存在する事前確率であり、誤警報と見逃したターゲットによる平均損失を決定します[2]。 たとえば、この基準を使用して火災警報のしきい値を設定する場合、誤警報が発生した場合のリスクのコストは、火災サービスを呼び出すことであり、合格した場合、燃え尽きたアパートやオフィスの物のコストです。



図1は、信号がある場合とない場合の確率密度分布のグラフを示しています。また、判定を行う際のエラーの確率に数値的に等しい面積を持つゾーンも強調表示されています。 この例で考慮される現象の確率的性質により、分布の分散はゼロではありません。 最小平均リスクの基準によれば、信号を検出するための最適なアルゴリズムは、r̅が最小のアルゴリズムです[2]。

最大事後確率の基準（最大尤度）

この基準は、エラーによる損失が発生確率C_01 = 1 / P {d_0}、C_10 = 1 / P {d_1}に反比例する場合、最小平均リスクの基準から取得されます。 この場合、最適な検出器しきい値は、エラー確率P_osh = P {d_0 / H_1} + P {d_1 / H_0}の合計を最小化するように設定されます（図2を参照）。





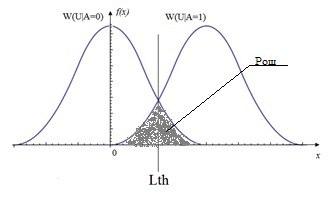
図2 Wの存在（U | A = 1）とWの不在（U | A = 0）の条件付き確率密度の分布とエラーの確率のグラフ

Waldの2つのしきい値テスト

複数のチャネルと1つの検出器または円形レーダー調査がある場合など、プロセス監視時間が大きな役割を果たす場合、2しきい値とも呼ばれるWaldの仮説の逐次検証の基準が使用されます。





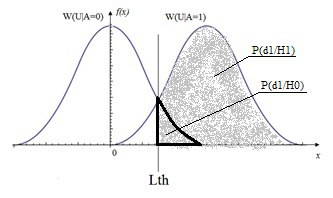
図3 Wの存在（U | A = 1）とWの不在（U | A = 0）の条件付き確率密度の分布と正しい検出の確率と誤警報の確率のグラフ



この基準によれば、確率ドメインは3つのサブドメインに分割され、2つのしきい値で分割され、正しい検出と誤警報の確率によって決定されます（図3を参照）。

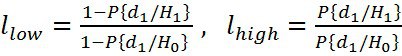
Waldの基準は、多数の実験の平均観測時間を最小化するという意味で最適です[4]。 レーダーが検出手順の期間を短縮することが最も望ましいため、現代の現実はこの基準のますます積極的な使用につながっています[5]。

ノイマンピアソン検定

ベイズのクラス基準の大きなマイナス点は、損失マトリックスの要素のアプリオリな知識の必要性です。 たとえば、敵の爆撃機が北軍の領土に侵入した場合、リスクのコストは計算できません。



Neumann-Pearsonテストは、検出時間を記録します。 最適なアルゴリズムは、P {d_1 / H_1}の正しい検出の最大確率を使用します。ただし、誤ったアラームP {d_1 / H_0}の確率が所定の値を超えない[6]。



Neumann-Pearson基準は、状況A = 1およびA = 0のアプリオリ確率の知識を必要としないという事実を考慮して、主要なものの1つとしてレーダーで使用されます[5]。

おわりに

検出器を開発するときは、最適化基準を意識的に選択することが非常に重要です。すでに述べたように、各基準は特定の状況で最大のパワーを持ち、他の基準を使用すると望ましくない結果につながる可能性があるためです。



使用されるソースのリスト：



[1] Bulyakulov RR適応型しきい値デバイス// 2014 IEEE North West Russia Section Young Researches in Electrical and Electronic Engineering Conferenceの処理。 P.165。

土井：10.1109 / EIConRusNW.2016.7448237

[2]バクレフ、P.A。 レーダーシステム。 高校向け教科書/ P.A. バクレフ; M .:ラジオエンジニアリング、2004年-46ページ

[3]ユーレヴィチ、E.I。 自動制御の理論/ E.I. ユレビッチ; M。：エネルギー、1969

[4]ボガチレフ、AA 品質管理の統計的手法の標準化/ A. A.ボガティレフ、Yu。D.フィリッポフ; M。：標準の出版社、1989年-42ページ

[5]クラメンコフ、A.S。 Neumann-Pearson基準および逐次確率比基準/.に基づくレーダー探知機の比較分析。 S.N.クラメンコフ Yarmolik // BSUIR No. 6（76）Minsk、2013のレポート。

[6]バシリエフ、K.K。 信号処理の方法：Textbook / K.K. ワシリエフ; ウリヤノフスク、2001年。