シンボリック回帰は非常に興味深いと考えられています。 「問題を解決するのに最適な機能を見つけてください。」 そして、Habréで私はすでに、この問題に適用される進化アルゴリズムの1つを著者が検討した投稿に出会いました( ここにあります )。
遺伝的プログラミングは確かに強力な方法です。 しかし、この記事では、別の(それほど面白くない)メソッドを検討します-文法進化。 私はそれについて長い間話さないでしょう。 この方法では、Bacus-Naurの形式の自由文法と、「エンジン」としての進化アルゴリズム(遺伝的アルゴリズムを選択しました)を使用しているとしか言えません。 そして、この方法はとてもクールです!
例に直行します。 主力製品として、私はDuffing Oscillatorを選択しました。
タスクについて説明します。 2次の不均一微分方程式があります。
私たちはそれを均質にします(非定型OD):
方程式を通常のコーシー形式に簡約した後、次のシステムを取得します。
させる および初期条件のベクトル
初期条件のベクトルは[1,1]に等しくなります。 目的:最短時間でシステムを状態[1,1]から[0,0]に転送するような関数u(t、x)を取得します。
差分システムコード:
Duffing = [ lambda t,x: x[1], lambda t,x: -x[0] - x[0]**3 + u(t,x) ]
私がメソッドに選んだ文法を考慮することは残っています:
grammar = { '<expr>' : [ '(<expr>)<op>(<expr>)', '<val>', '<func1>(<expr>)' ], '<op>' : [ '+', '-', '*', '/' ], '<val>' : [ 'x2', 'x1', '(smallConst)', '(bigConst)' ], "<func1>": [ 'minus','math.sin', ] }
プリミティブですが、望ましい結果が得られます。 smallConstは区間[0,1]の定数であり、bigConstは区間[0,200]の定数であることに注意してください。
パラメーターを使用して遺伝的アルゴリズムを実行する
染色体の長さ(染色体上の各数字は0から200の範囲の整数値)= 10
人口の長さ= 50。
反復回数(進化の期間)= 200。
次の結果が得られます。
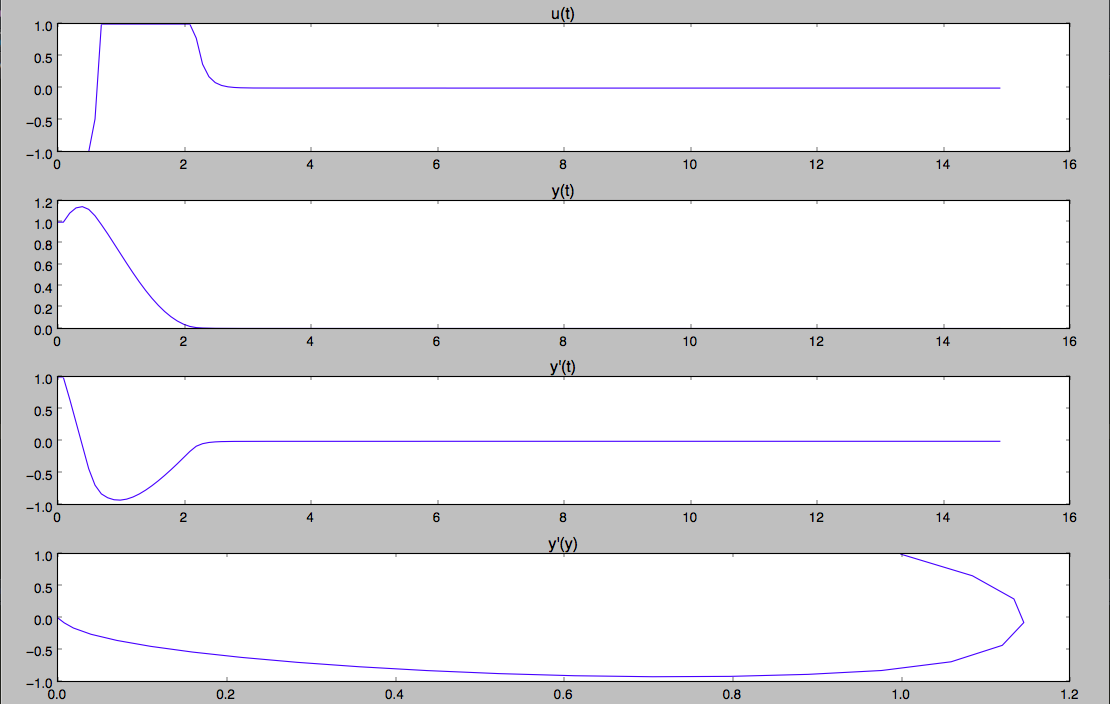
2.5秒は一時的な時間です。
u(t、x)=((マイナス(x2))-((x1) ((0.69028)))) ((11))(かなり明確なビューですが、多くの括弧があります)
平均過渡時間を取得するには、アルゴリズムを複数回実行する必要があります(これは明らかです)。 しかし、この記事では、アルゴリズムが機能し(!!)、結果が得られることを示したいと思いました。
結論:文法進化は、シンボリック回帰の問題を解決するための若いが強力なツールです。 はい、解決される問題に対して特定の文法を選択する数学的に正確な方法はありません。 経験と試行錯誤に頼る必要があります。 しかし、この方法は機能し、多くの場合、最適化された文法なしで許容可能な結果を生成します。
誰かがGEに興味を持っているなら、このメソッドの作者による記事があります (多分、すぐに翻訳します)。