😥 ☕️ 👂🏿 GF最終フィールド（256）といくつかの魔法 👨🏽‍🎓 👍🏾 🕑

はじめに

学生として、私は暗号学のクラスに参加しています。そしてもちろん、このコースはAES標準を無視できませんでした。

このアルゴリズムを実装するとき、GFフィールド（2 ^ 8）の実装の問題が発生します。これについては、この記事で取り上げます。考慮されます：フィールド要素の乗算のビットマジック、コンパイル段階で置換テーブルを生成するためのテンプレート。

2番目の部分は、読者がC ++ 14をサポートするコンパイラーにアクセスできることを前提としています。最初の部分はCスタイルで記述されます。

最終フィールドは何ですか

https://ru.wikipedia.org/wiki/Endフィールド

GFフィールド（p）

最初に、単純な要素GF（p）を持つフィールドがどのように形成されるかを考えます。

その要素は数字です $\ {0、1、...、p-1 \}$ 。加算および乗算演算-pを法とする加算および乗算

たとえば、p = 7の場合：

2 + 6 = 8％7 = 1

4 * 3 = 12％7 = 5

フィールドGF（p ^ q）

フィールドGF（p）に基づいて、より一般的なフィールドGF（p ^ q）が構築されます。pは単純で、qは自然です。

そのような体の要素は体GF（p）上の多項式です：

$\ {0、1、2、\ ldots、p-1、x、\ ldots（p-1）x、...、x ^ {q-1}、\ ldots、（p-1）x ^ {q -1} \}$

このフィールドでの加算は、これらの多項式の直接加算になります。

たとえば、p = 2、q = 3の場合：

$（x + 1）+（x ^ 2 + 1）=（x ^ 2 + x）$

乗算は少し難しいです。それを決定するためには、GF（p）で既約である次数qの多項式Q（x）が必要です（与えられた積を与える次数の低い2つの多項式はありません）。幸いなことに、pとqにはこのような多項式が存在します。

多項式Q（x）が選択されている場合、フィールドの2つの要素a * bの積を求めるには、次が必要です。

それらの多項式の積を見つけるa（x）* b（x）
この積を多項式Q（x）で除算した余りを求めます。これはa * b

たとえば、p = 2、q = 3の場合：

Q（x）= x ^ 3 + x + 1（既約多項式）

a = x ^ 2 + 1、b = x ^ 2

a（x）* b（x）= x ^ 4 + x ^ 2

（x ^ 4 + x ^ 2）％Q（x）=（x ^ 4 + x ^ 2-x * Q（x））％Q（x）=（x ^ 3 + x）％Q（x）= （x ^ 3 + x-Q（x））％Q（x）= 1 = a * b

p = 3の場合、q = 2

Q（x）= x ^ 2 + x + 2（既約多項式）

a = x + 2

b = 2x + 2

a（x）* b（x）= 2 x ^ 2 +（6％3）* x +（4％3）= 2 x ^ 2 + 1

（2 x ^ 2 + 1）％Q（x）=（2 x ^ 2 + 1-2Q（x））％Q（x）=（（-2％3）x +（-3％3））％ Q（x）= x％Q（x）= x

実装

そのため、多項式x ^ 8 + x ^ 4 + x ^ 3 + x + 1上の体GF（256）で次の演算を実装する必要があります。

乗算
反対を見つける

フィールド要素の積から始めましょう：

最初に頭に浮かぶのは、単純なアルゴリズムで多項式の積を実装することです。

uint16_t polynomeMul(uint8_t a, uint8_t b){ unsigned rez = 0; for(int i=0; i<8; ++i){ rez ^= a * b&(1<<i) //    2  b_i * (x^i) * a(x) } return rez; }

次に、多項式による除算の剰余を見つけるための関数を記述します。

この瞬間、私は次に何が起こるのだろうと思いました。そして、私は多項式の拡張ユークリッドアルゴリズムを待っていました。実際、それほど怖くはありませんでしたが、考えることにしました。しかし、何とかそれを美しく行うことは可能ですか？ 1つの演算を使用してこのような2つの多項式を乗算し、別の除算の剰余を見つけることができないのは残念です。

しかし、それは本当に不可能ですか？単純な積で多項式の積を実現するのを妨げるものを見てみましょう。

多項式の積の式により、次のようになります。

$（\ sum_i a_i * x ^ i）*（\ sum_i b_i * x ^ i）= \ sum_i \ sum_ {n = 0} ^ {i} a_n b_ {i-n} x ^ i$

バイナリシステムの2つの数値の積について、ほぼ類似した式が得られます。

$（\ sum_i a_i * 2 ^ i）*（\ sum_i b_i * 2 ^ i）= \ sum_i \ sum_ {n = 0} ^ {i} a_n b_ {i-n} 2 ^ i$

違いは、多項式の場合、式 $\ sum_ {n = 0} ^ {i} a_n b_ {i-n}$ の係数を決定します $x ^ i$ 。

前のカテゴリではオーバーフローが発生し、対象の値が変更される可能性があるため、同様の数値のステートメントは当てはまりません。

オーバーフローを取り除く方法は？とても簡単です。次のエントリを検討してください。

$（\ sum_i a_i * 2 ^ {4i}）*（\ sum_i b_i * 2 ^ {4i}）= \ sum_i \ sum_ {n = 0} ^ {i} a_n b_ {i-n} 2 ^ {4i}$

7を超えない次数の多項式を乗算する場合、14を超える次数の多項式を取得することは不可能であるため、カテゴリは15以下のゼロと1の合計に対応します（実際には、オーバーフローが不可能であることを確認するのは簡単です）。直接量をモジュロ2の合計に変換するためだけに残り、最下位ビットを強調表示します。

したがって、各ブロックが4ビットのブロックに対応する数として多項式を表す場合、積は次のように記述できます。

 uint64_t polynomeMul(uint64_t a, uint64_t b){ return (a*b) & 0x1111111111111111; // & 0b0001000100010001... }

次に、積をガロア体の要素として分析します。

多項式を見てみましょう $x ^ 8 + x ^ 4 + x ^ 3 + x + 1$ 。選択したビューでは、q = 0x100011011のようになります。肉眼では、最も古いブロックの直後に多数のゼロブロックが表示されます。 Q（x）が次の形式の多項式で乗算される場合 $x ^ n（a_0 + a_1 * x + a_2 * x ^ 2 + a_3 * x ^ 4）$ 多項式を取得します：

$x ^ {n + 8}（a_0 + a_1 * x + a_2 * x ^ 2 + a_3 * x ^ 4）+ \ sum_i ^ {n + 7} b_i x ^ i$

または、古いブロックが $a_0、a_1、a_2、a_3$ 。これを使用して乗算関数を記述します。

 uint64_t galoisMul(uint64_t a, uint64_t b){ uint64_t mul = polynomeMul(a, b); const uint64_t basePolynome = 0x100011011; mul ^= polynomeMul(basePolynome, mul>>48<<16); //   Q(x)      (  4 ),     12   mul ^= polynomeMul(basePolynome, mul>>32); //        8 ,    .         mul. return mul; }

乗算を整理します。次に、その逆要素を見つける方法を学ぶ必要があります。

追加と0のないフィールドは255個の要素のグループを形成することを思い出してください。これは、任意の要素xに対して、この要素によって形成されるサブグループのサイズに等しい数rがあり、x ^ r = 1であることを意味します。サブグループの順序はグループの順序の約数であるため、 $x ^ {255} = x ^ {kr} =（x ^ r）^ k = 1$ 、それは次のようになります $x * x ^ {254} = 1$ 。次に、逆要素の定義に従って、 $x ^ {-1} = x ^ {254}$ ：

 uint64_t galoisPow(uint64_t a, unsigned n){ //    . if(n==0){ return 1; }else if(n%2 == 0){ return galoisPow(galoisMul(a, a), n/2); // (a*a)^(n/2) }else{ uint64_t square = galoisMul(a, a); return galoisMul(galoisPow(square, n/2), a); // a * (a*a)^[n/2] } } uint64_t galoisInverse(uint64_t a){ return galoisPow(a, 254); }

それだけですか？ああ、元のバイトをすべての操作を実行する拡張形式に変換できる必要があります。これはサイクルで額にできますが、今日ではできません。内なる声は、汚いトリックを使う必要があると言っています。最後に、単一ビットのカウントについての記事を徹底的に読みませんでしたか？

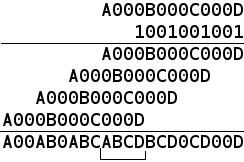
バイトを0bABCDEFGHとして示します。最初に思い浮かぶのは、3つの最下位ビットの0b1001001による乗算です。

0bFGH * 0b1001001 = 0bFGHFGHFGH

0bFGHFGHFGH | 0b100010001 = 0bF000G000H、または3つの最下位ビットが所定の位置に落ちました。

同様に、中央の3ビットと最上位のペアで行われます。トリックが発明されました。しかし、3つの乗算はどういうわけか多すぎます。 4ビットごとに同じことを行うことは可能ですか？多数のビットのサンプルを調べた結果、私はそれが機能する4つだけを見つけることができました。

ブロックの下位ビット7、6、1、0に注意してください。それらは、その場所に目的のビットが存在すること、そして最も重要なこととして、最下位（データに対して）ビットによるオーバーフローの不可能性によって特徴付けられます。

言われたように、私は2対の4を見つけませんでした。失敗？そうでもない。 2つの乗算を使用して8ビットのうち7ビットを配置できる場合、8つすべてを配置し、最後のビットを単純なシフトでその場所に配置できます。

 uint64_t extendToGalois(uint8_t a){ return (a & 0xC3) * 0x249249 & 0x11000011 | (a & 0x1C) * 0x1240 & 0x00011100| (a & 0x20) << 15; }

圧縮が簡単です。次の乗算は、4ビットを圧縮する方法を示しています。

これを念頭に置いて、コードは次の形式を取ります。

 uint8_t shrinkFromGalois(uint64_t a){ return (a & 0x11110000) * 0x249 >> 21 & 0xF0 | (a & 0x00001111) * 0x249 >> 9 & 0x0F; }

コンパイラに考慮させる

事前に計算されたテーブルを使用できるのに、なぜ非常に高価なバイト変換を使用するのですか？このセクションでは、追加による逆要素の表の例を使用して、テンプレートマジックを使用してコンパイル段階で計算する方法を説明します。

まず、以前に記述されたすべての関数にconstexpr指定子を追加します（これ以降、コンパイルにはC ++ 14のサポートが必要になります）。これにより、これらの関数をテンプレート引数として使用できます。

 //      contexpr static uint8_t inverse(uint8_t x){ return shrinkFromGalois(GaloisInverse(extendToGalois(x))); } <p>template<int N, int… Data> class GaloisTable{ public: static constexpr auto& data = GaloisTable<N-1, inverse(N-1), Data…>::data; }</p> <p>template<int… Data> class GaloisTable<0, Data…> public: static constexpr uint8_t data[] = {Data…}; }</p> <p>template<int… Data> constexpr uint8_t GaloisTable<0, Data…>::data[];</p>

GaloisTable <256> ::データを使用しようとするとどうなるかを考えてください。

コンパイラーは、データがGaloisTable <255、inverse（255）> :: dataとして定義されている適切なテンプレート特殊化を見つけます。同様に、GaloisTable <254、逆（254）、逆（255）> ::データなどで定義されます。

各ステップで、次の形式のパターンがあります：GaloisTable <m、inverse（m）、inverse（m + 1）、...、inverse（255）>。そして、mが0に達するまで続きます。

mが0に達すると、コンパイラーはテンプレートのより具体的な特殊化を見つけることができます（コンパイラーは常により具体的なものを好みます）。次に、クラスの再帰タスクが完了し、Dataのシーケンスから...配列自体が作成され、以前のすべてのクラスによって借用されます。

このステップでのデータ...は、必要なインバース（0）、インバース（1）、...、インバース（255）にすぎません。

結論：結果として、私は素朴な実装に費やす時間よりもかなり多くの時間を費やしました（ただし、作業の大部分は記事自体のセットを使用していました）。したがって、アイデアが考えられるようになったら、考える価値があるかどうかを考えるのは理にかなっています。

この記事がお役に立てば幸いです。

更新： GaluaプレフィックスがGaloisに置き換えられました。

GF最終フィールド（256）といくつかの魔法

はじめに

実装

コンパイラに考慮させる

More articles: