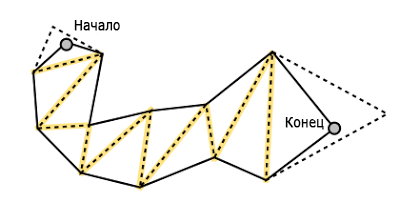
ファンネルアルゴリズムは、「ポータル」を通る最も単純なパスを見つけるための単純なアルゴリズムです。 最も詳細な説明は、 Efficient Triangulation-Based Pathfinding ( 2 )リンクで見つけることができます
ここでは、このアルゴリズムは単純に愚かに実装されます。 キューやその他のクールなものを使用する代わりに、最も単純な実装では、別の角度を検出するたびにループを再起動します。 つまり、一部のポータルは、必要以上に頻繁に尋問されますが、実装はより簡単になります。
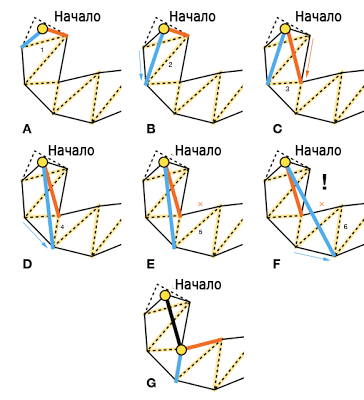
上記のキャンバスは、このアルゴリズムの6つのステップを示しています。 ポータルのすべてのファセット(黄色の何かにあるアリ)をチェックすると、次のアクションが実行されます。
- 左右のポイントが現在のトンネル内にあるかどうかを確認します。 はいの場合、何もせずに続行します(AD)。
- 新しい左ポイントがトンネルの外側にある場合、トンネルは更新されません(EF)
- 新しい左ポイントがトンネルの右端を超えている場合(F)、トンネルの右ポイントをパスのコーナーとして追加し、この(左)ポイントを開始ポイントとして設定および設定し、アルゴリズムを再起動します(G)。
これらの規則は左側に適用されます。
上記の例からわかるように、一部の面は数回再チェックされますが、これらの計算はすべて非常に単純であるため、オーバーヘッドが無視できるため、出力は単純で実用的な実装になります。
ひそかに隠されたコード
ポータル配列には、単純化するパスのすべてのポータルセグメント(左側の最初のフェースポイントと右側の最初のフェースポイント)が含まれます。 最初の右および最初の左のポイントは開始点であり、最後の左および右のポイントは終了点です。 つまり このようなもの:
inline float triarea2(const float* a, const float* b, const float* c) { const float ax = b[0] - a[0]; const float ay = b[1] - a[1]; const float bx = c[0] - a[0]; const float by = c[1] - a[1]; return bx*ay - ax*by; } inline bool vequal(const float* a, const float* b) { static const float eq = 0.001f*0.001f; return vdistsqr(a, b) < eq; } int stringPull(const float* portals, int nportals, float* pts, const int maxPts) { // . int npts = 0; // float portalApex[2], portalLeft[2], portalRight[2]; int apexIndex = 0, leftIndex = 0, rightIndex = 0; vcpy(portalApex, &portals[0]); vcpy(portalLeft, &portals[0]); vcpy(portalRight, &portals[2]); // . vcpy(&pts[npts*2], portalApex); npts++; for (int i = 1; i < nportals && npts < maxPts; ++i) { const float* left = &portals[i*4+0]; const float* right = &portals[i*4+2]; // . if (triarea2(portalApex, portalRight, right) <= 0.0f) { if (vequal(portalApex, portalRight) || triarea2(portalApex, portalLeft, right) > 0.0f) { // . vcpy(portalRight, right); rightIndex = i; } else { // , , vcpy(&pts[npts*2], portalLeft); npts++; // . vcpy(portalApex, portalLeft); apexIndex = leftIndex; // vcpy(portalLeft, portalApex); vcpy(portalRight, portalApex); leftIndex = apexIndex; rightIndex = apexIndex; // i = apexIndex; continue; } } // . if (triarea2(portalApex, portalLeft, left) >= 0.0f) { if (vequal(portalApex, portalLeft) || triarea2(portalApex, portalRight, left) < 0.0f) { // . vcpy(portalLeft, left); leftIndex = i; } else { // , , . vcpy(&pts[npts*2], portalRight); npts++; // vcpy(portalApex, portalRight); apexIndex = rightIndex; // vcpy(portalLeft, portalApex); vcpy(portalRight, portalApex); leftIndex = apexIndex; rightIndex = apexIndex; // i = apexIndex; continue; } } } // . if (npts < maxPts) { vcpy(&pts[npts*2], &portals[(nportals-1)*4+0]); npts++; } return npts; }
// vcpy(&portals[nportals*4+0], startPos); vcpy(&portals[nportals*4+2], startPos); nportals++; // for (int i = 0; i < path->npolys-1; ++i) { getPortalPoints(mesh, path->poly[i], path->poly[i+1], &portals[nportals*4+0], &portals[nportals*4+2]); nportals++; } // vcpy(&portals[nportals*4+0], endPos); vcpy(&portals[nportals*4+2], endPos); nportals++;
蜂蜜の樽に蜂蜜を一滴入れると、このアルゴリズムは任意のナビゲーション形式のコンテキストで実装できます。 グリッド、接続された正方形、四分木、ウェイポイント(ウェイポイント)またはnavmesh-重要ではありません。1つのノードから別のノードへのポータルであるセグメントのリストを提供できることです。
また、アルゴリズムは攪拌とうまく組み合わされます。 次のターンに基づいて、希望する移動速度を自由に計算できます。 非常に高速であるため、ステッピングステップを適用する前に各反復で読み取ることができます(速度)。
ps少なくとも斜めに(翻訳者から)より完全なバージョンを知ることを強くお勧めします。