🥈 ⏪ 🧔🏻 普遍的なレーベンシュタインオートマトンを使用した辞書でのファジー検索。パート1 🍙 👦🏽 👋🏽

ファジィ文字列検索は、特に結果の高い精度が必要な場合、計算リソースの面で非常に高価なタスクです。この記事では、辞書のファジー検索アルゴリズムについて説明します。このアルゴリズムは、100％の精度と比較的低いメモリ消費を維持しながら、高い検索速度を提供します。 Lucene開発者がファジー検索の速度を2桁上げることができたのは、Levenshteinオートマトンでした

はじめに

辞書内の文字列のファジー検索は、テキストエディター、光学式文字認識システム、および検索エンジンで使用される最新のスペルチェックシステムを構築するための基盤です。さらに、ファジー検索は、バイオインフォマティクスの多くの計算上の問題を解決するためのアプリケーションを見つけます。

辞書のファジー検索問題の正式な定義は、次のように定式化できます。与えられた検索クエリWに対して、検索クエリとの差pが特定のしきい値Nを超えないすべての単語のサブセットPを辞書Dから選択する必要があります。

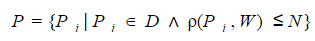
2つの単語の違いの程度は、たとえば、レーベンシュタイン距離またはダメラウ-レーベンシュタイン距離を使用して測定できます。

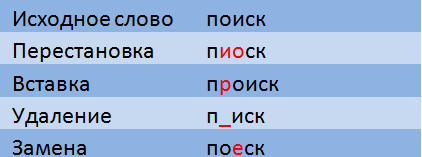
レーベンシュタイン距離は、2行間の差の尺度であり、1行を別の行に変換するために必要な文字の挿入、削除、および置換の最小数として定義されます。

Damerau-Levenshtein距離を計算するとき、転置（2つの隣接する文字の順列）も許可されます。

数年前、Habréには、辞書とテキストのファジー検索専用のntzからの投稿がありました-レーベンシュタインとダメラウ-レーベンシュタインの距離に関する詳細はここで読むことができます。状態をチェックする時間の複雑さを思い出すだけです

動的計画法を使用したp（P _i 、W）<= Nは、

、

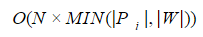ここで| P _i |、| W | -文字列とリクエストの長さ。したがって、実際の問題を解決する場合、各単語の検証を伴う辞書値の完全な列挙は、原則として受け入れられません。

すべてのファジー検索アルゴリズムが、クエリWによって、条件p（P _i 、W）<= Nを満たす辞書Dのすべての絶対単語が見つかることを保証するわけではないことに注意してください。したがって、検索の精度については、見つかった結果の数と、特定の条件を満たす辞書内の実際の単語数との比として説明するのが理にかなっています。たとえば、すでに言及した投稿の著者は、n-gram法を使用した検索の精度を65％と推定しました。

非決定性レーベンシュタインオートマトン

著者は、読者がオートマトンおよび形式言語の理論の基礎に精通しており、この主題分野の用語の説明を控えることを前提としています。代わりに、すぐに仕事に取り掛かります。

実用的な問題を解決するために、レーベンシュタインの決定論的な有限状態マシンが使用されます（完全に正確に言えば、その模倣）。ただし、レーベンシュタインの確定的有限状態マシンの動作原理を理解するには、まず非確定的バージョンの動作を検討することをお勧めします。

単語Wのレーベンシュタインオートマトンとは 、単語WとSの間のレーベンシュタイン（Damerau-Levenshtein）距離が指定された値Nを超えない場合にのみ、単語Sを取る有限オートマトンA _N （W）を意味します。

単語Wおよび許容される変更数Nのレーベンシュタインステートマシンは、順序付けられた5つの要素A _N （W）= <E、Q、q ₀ 、F、V>として定義できます。ここで、

Eはオートマトンのアルファベットです。

Qは内部状態のセットです。

q _0-初期状態。集合Qに属します。

Fは最終状態または最終状態のセットです

Vは遷移関数で、オートマトンの入力に別のシンボルが到着したときに現在の状態からどの状態を遷移できるかを決定します。

非決定性のレーベンシュタインオートマトンA _N （W）の状態は 、通常i ^#eとして示されます。ここで、 i = 0 .. | W | 、 e = 0..N 。マシンの状態がi ^#eの場合、 iは「正しい」文字がマシンに入力され、 e個の変更が検出されたことを意味します。転置をサポートするオートマトン（つまり、 Damerau-Levenshtein距離がp（S、W）として使用される）を考慮するため、状態のセットは状態{i _T ^#e }で補完する必要があります（ i = 0 .. | W | -1 、 e = 1..N

オートマトンの初期状態は状態0 ^＃0です。

最終状態のセットには、条件| W | -i <= N-e 。

オートマトンの状態の物理的な意味に基づいて、許容可能な遷移の構成を決定することは難しくありません。レーベンシュタインオートマトンの遷移関数は、テーブルの形式で指定されます。

オートマトンの状態の構成の厳密な数学的正当化と上記のその他の論文に興味がある場合は、Schultz and Mikhov（2002）の記事でそれを見つけることができます。

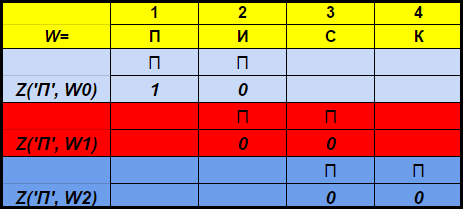
文字xの特性ベクトルZ（x、W _i ）は、長さmin（N + 1、| W |-i）のビットベクトルです。文字列Wの（i + k）番目の文字がxの場合、 k番目の要素は1です、それ以外の場合は0 。たとえば、 W =” LIST”の場合

Z（ ''、W ₀ ） = <1、0>、およびZ（ ''、W ₁ ） = <0、0>。

W =“ LIST”およびN = 1のレーベンシュタインオートマトンのグラフィカルな表現を図に示します。オートマトンの遷移は、対応する特性ベクトルによって署名されます。

オートマトンの最終状態は緑色で強調表示されます。水色-マシンの現在の（アクティブな）状態。

水平矢印に沿った移行は、「正しい」記号が機械に入力されると実行されます。

垂直矢印に沿った遷移は、マシンに入力された次の文字が（i + 1）番目の文字の前に元の単語Wに挿入されるという仮定に対応しています。垂直矢印に沿って移動すると、オートマトンは単語Wの変更を「検出」します。eの値は1増加します。

状態i ^#eから状態（i + 1） ^＃e + 1への遷移は、次の文字が単語Wの （i +1）番目の文字を置き換えるという仮定に対応します。

状態i ^#eから状態（i + 2） ^＃e ^{+ 1}への遷移は、次の文字が単語Wの（i + 2）番目の文字に対応し、単語Wの（i + 1）番目の文字が欠落しているという仮定に対応します単語Sで

おそらく、状態i _T ^#eへの遷移は、単語Wの（i + 1）番目と（i + 2）番目の文字の転置が検出されたことを示唆していることをすでに推測しているでしょう。

それでは、その仕組みを見てみましょう。曲線の赤い矢印でマシンへの新しいシンボルの入力を示し、矢印の右側に特性ベクトルの値を示します。これは、「SEARCH」という単語を入力すると、マシンA ₁ （「LIST」）がどのように機能するかを示しています。

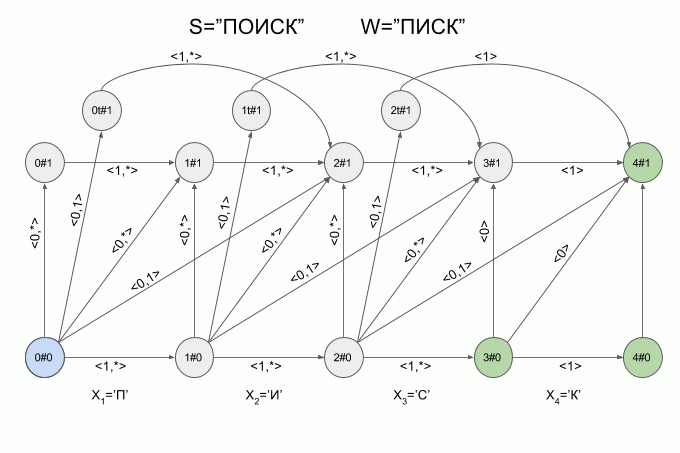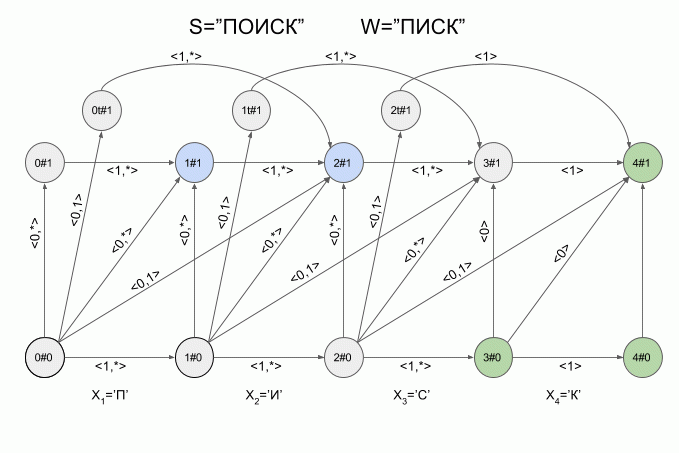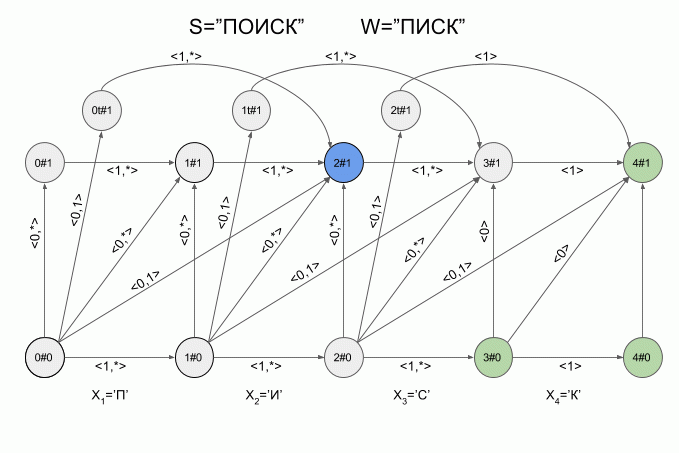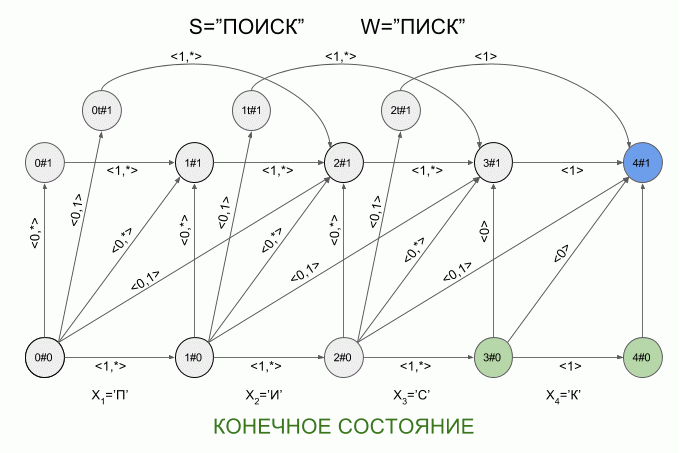
実際、オートマトンの状態の変化のシーケンスは、オートマトンの入力に供給される特定の単語ではなく、特性ベクトルのシーケンスによってのみ決定されることに注意してください。このシーケンスは、2つの異なる単語で同じ場合があります。たとえば、オートマトンが「mother」という単語に設定されている場合、特性ベクトルのシーケンスは「lama」、「frame」、「lady」などの単語で同じになります。

別の興味深い事実は、オートマトンの許容可能な遷移の構造がi = 0の場合に変化しないことです。..| W | -（N + 1） 。

これらの2つの状況により、ファジー検索アルゴリズムのソフトウェア実装は、特定の単語ごとに計算されるのではなく、その普遍的な模倣のマシンを使用できます。それが、投稿のタイトルが「普遍的な」レーベンシュタインオートマトンを指す理由です。

この場合、特定の単語Sのオートマトンの計算は、単語Sの各シンボルxの特性ベクトルの単純な計算に削減されます。状態の変更は、2つの変数eの単純な増加としてソフトウェアに実装されます。 Schulz and Mihov（2002）は、単語Sのすべての特性ベクトルが時間O（| S |）で計算できることを示しました。これは、マシンの一時的な複雑さです。

単語Sの文字は、機械の入力に順次送られます。特定のキャラクターを給餌した後、ラインSとWの間の距離がしきい値Nを超えることが明らかになった場合、マシンは「空の」状態にあり、マシンにはアクティブな状態はありません。この場合、単語Sの残りの文字の特性ベクトルを計算する必要がなくなります。

これは、マシンがW = "LIST"で単語S = "ICS"を「実現」する方法です。

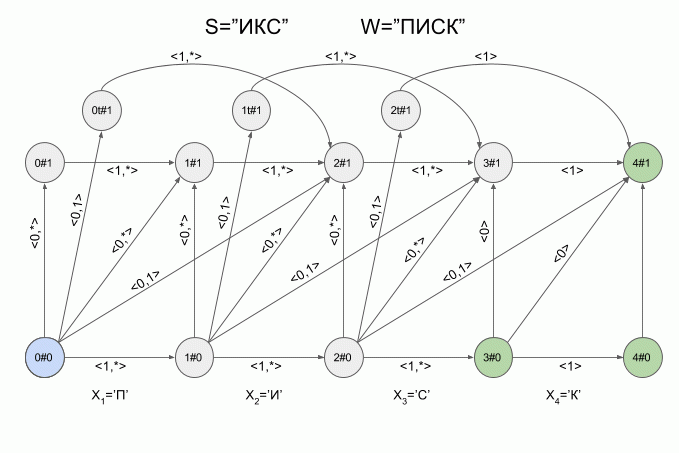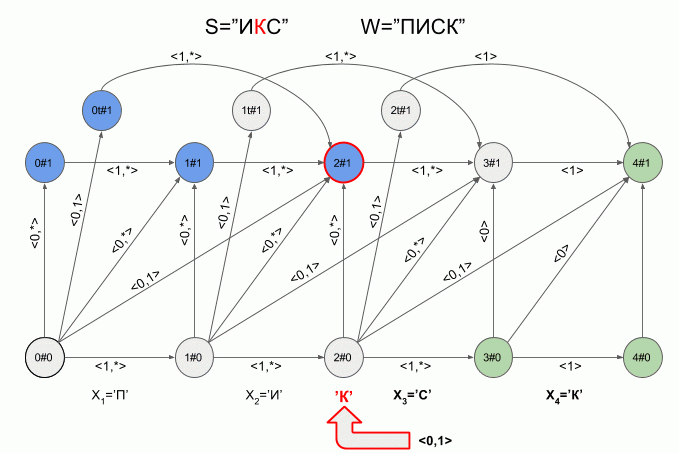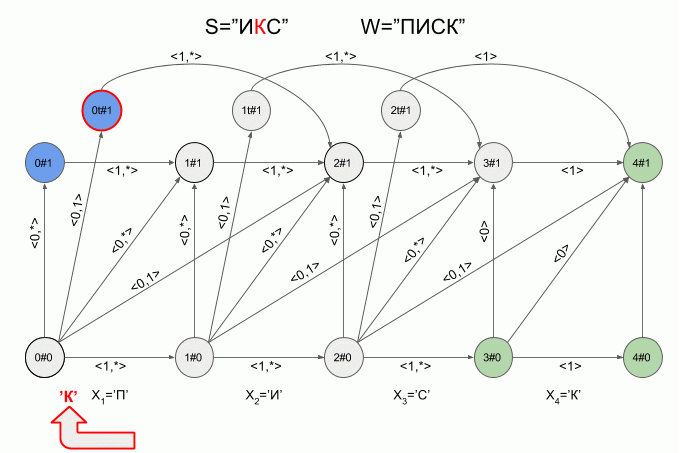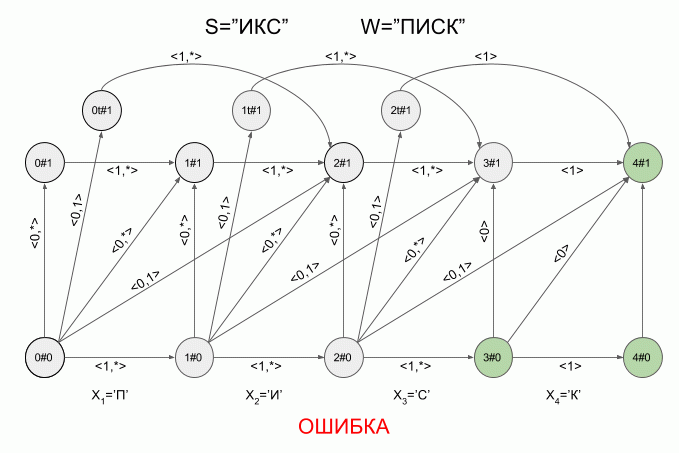
「I」記号を入力した後、4つのアクティブ状態がマシンにすぐに現れましたが、「K」記号を入力した後、アクティブ状態はありませんでした。マシンはエラー状態で、「IKS」という単語を受け入れませんでした。この場合、シンボル「C」の特性ベクトルの計算は実行されませんでした。

決定論的レーベンシュタインオートマトン

決定論の定理に従って、非決定論的有限状態機械について、同等の決定論的有限状態機械を構築できます。決定論的オートマトンが必要なのはなぜですか？ソフトウェアを実装するだけで、より速く動作します。主に、現在の状態を1つしか持てないため、次の文字を入力するときに、特性ベクトルを1つだけ計算し、遷移テーブルから遷移を1つだけ決定する必要があります。

上記で検討した非決定論的レーベンシュタインオートマトンA ₁ （W）について、特徴ベクトルのすべての可能な値を順番に繰り返す場合、次のセットのいずれかを構成する状態が同時にアクティブになることを確認できます。

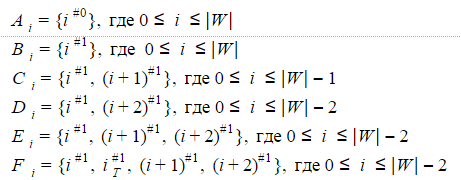
上記の6つのセットは、 N = 1の確定的レーベンシュタインオートマトンの状態になります。より正確には、オートマトンには、 i = 0 .. | W | -2の 6つの状態、 i = | W | -1の 3つの状態、およびi = | W | -1の 2つの状態があります。 。

決定性オートマトンの特性ベクトルの次元は、 2N + 1として計算できます。次に、 | W |からの単語のオートマトンの遷移表 N = 1の文字には、 ^{2x1 + 1}行2行と6x（| W | -1）+ 3 + 2列が必要です（たとえば、6文字の単語の場合は8x35）。さらに、このようなテーブルは、 | W |の各値に対して計算する必要があります。個別に。これはあまり便利ではなく、計算のための追加の時間またはストレージのための追加のメモリが必要です。

ただし、上で書いたように、オートマトンの許容可能な遷移の構成は、 i = 0の場合は変化しません。 -（2N + 1） 。したがって、ソフトウェア実装では、実際のオートマトンを計算する代わりに、決定論的オートマトンをシミュレートする方がはるかに便利です。これを行うには、オフセット値iを保存し、8行6列のユニバーサル遷移テーブルを使用するだけで十分です。このようなテーブルは事前に計算できます。

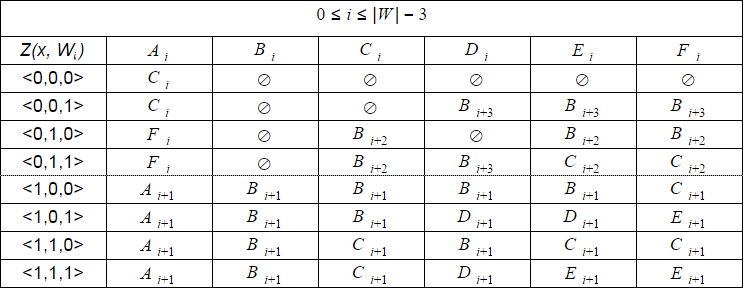
iが増加すると、オートマトンの一部の状態が到達不能になるため、 i = | W | -2 .. | W | 別の小さなテーブルを用意する必要があります。

さらに、決定論的なレーベンシュタインオートマトンといえば、まさに上記の普遍的な模倣を意味します。

Nが増加すると、状態の数は指数関数的に増加します。したがって、 N = 2の場合、確定オートマトンは42個の状態を持つことができます。N = 3の場合、すでに数百個あります。これは、メモリ消費がO（N ² ）に比例することを意味します。

決定論的レーベンシュタインオートマトンの初期状態は、状態A _0になります。

最終的な条件は何ですか？非決定的オートマトンの最終状態に対応するもの。 N = 1の場合、これらは状態A _{| W |} 、 B _{| W |} 、 A _{| W | -1} 、 C _{| W | -1} 、 D _{| W | -2} 、 E _{| W | -2} 、 F _{| W | -2} 。

6つの状態間の遷移の数は非常に多く、決定論的なレーベンシュタインオートマトンの状態の物理的な意味は明らかではないため、ここではそのグラフィカルな表現を示しません。全体像ははっきりしていないと思います。それでも彼女を見たい場合は、 Mikhov and Schulz（2004）の記事を参照してください。非決定的オートマトンの操作のもう1つの例を示しますが、今回は、どの状態でその決定的同等物がすべての瞬間に存在するかを示します。

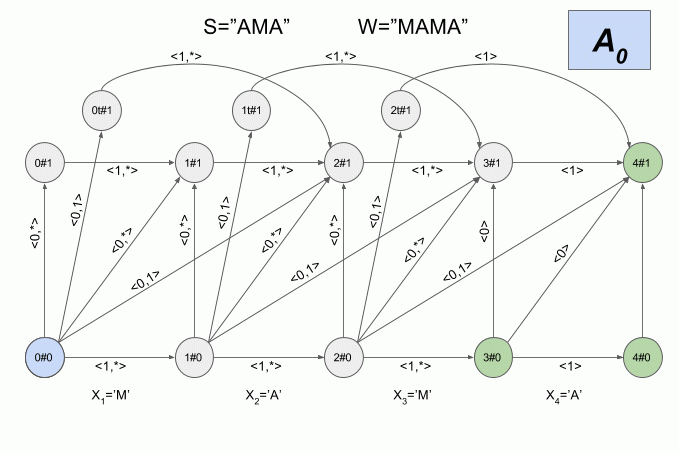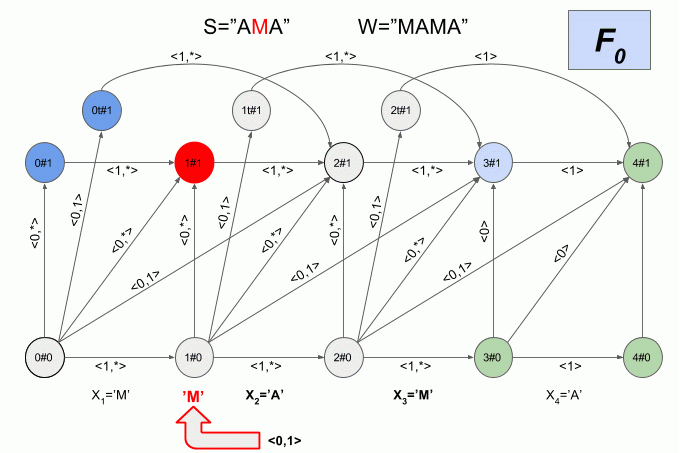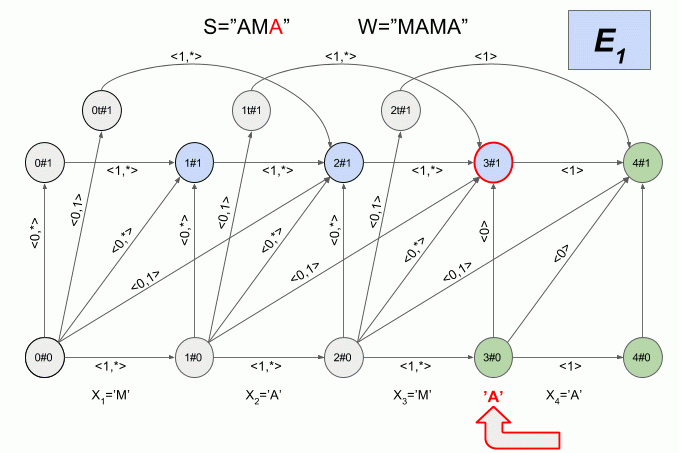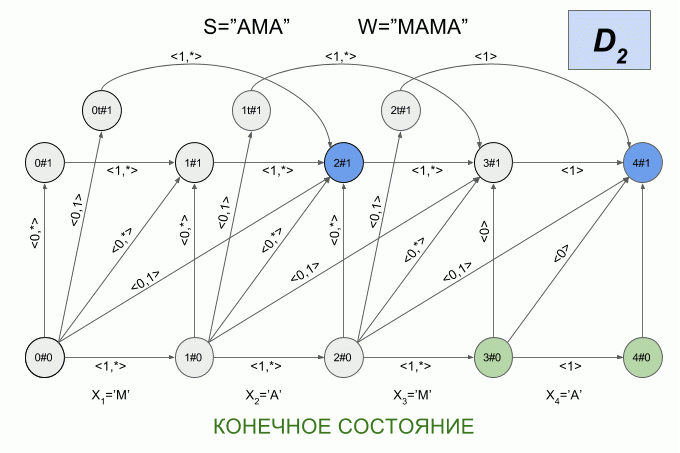
決定されたレーベンシュタインオートマトンのソフトウェア実装

レーベンシュタインオートマトンのソフトウェア実装をC＃で作成しました-この言語に最も精通しています。ここでソースを見つけることができます。ユニバーサル変換テーブルは、静的クラスParametricDescriptionのフィールドとして実装されます。このクラスには、 N = 1,2のユニバーサル変換テーブルが含まれています。

変換テーブルに加えて、ParametricDescriptionクラスにはオフセット増分テーブルも含まれています。オフセット増分は、次の状態に移行するときにiの値を増やす必要がある値です。

レーベンシュタインオートマトン自体は、LevTAutomataImitationクラスに実装されています。すべてのクラスメソッドは非常に単純であり、詳細に説明しません。辞書でファジー検索を実行する場合、リクエストごとにクラスのインスタンスを1つ作成するだけで十分です。

LevTAutomataImitationクラスのインスタンスの作成は、 W 、 S 、 Nの任意の値に対して短い一定時間で実行されることに注意してください。クラスインスタンスには、 Wの値と小さなサイズの補助変数のみが格納されます。

文字列の配列から、指定されたDamerau-Levenshtein距離から2以内の距離にある文字列のみを選択するには、次のコードを使用できます。

//Misspelled word string wordToSearch = "fulzy"; //Your dictionary string[] dictionaryAsArray = new string[] { "fuzzy", "fully", "funny", "fast"}; //Maximum Damerau-Levenstein distance const int editDistance = 2; //Constructing automaton LevTAutomataImitation automaton = new LevTAutomataImitation (wordToSearch, editDistance); //List of possible corrections IEnumerable<string> corrections = dictionaryAsArray.Where(str => automaton.AcceptWord(str));

与えられたコードは、レーベンシュタインオートマトン-網羅的検索のアルゴリズムを使用して、辞書で最も単純なファジー検索アルゴリズムを実装します。もちろん、これは最も効率的なアルゴリズムではありません。レーベンシュタインオートマトンを使用したより効率的な検索アルゴリズムについては、記事の後半で説明します。

参照資料

C＃の記事のソース
レーベンシュタイン距離
距離Damerau-Levenshtein
ステートマシン
辞書とテキストのあいまい検索に関する良い投稿
レーベンシュタインオートマトンの簡単な説明
Schultz and Mihov（2002）の記事でのレーベンシュタインオートマトンの詳細な数学的説明
同じトピックに関するMikhovとSchulz（2004）の別の記事
ファジー検索Luceneでのレーベンシュタインオートマトンの実装の歴史
Javaでの実装： 1と2
私の出版物の第二部

普遍的なレーベンシュタインオートマトンを使用した辞書でのファジー検索。 パート1

はじめに

非決定性レーベンシュタインオートマトン

決定論的レーベンシュタインオートマトン

決定されたレーベンシュタインオートマトンのソフトウェア実装

参照資料

More articles:

普遍的なレーベンシュタインオートマトンを使用した辞書でのファジー検索。パート1