ほとんどのプログラムとアルゴリズムは、一連の頂点（ N ）とエッジ（ E ）で構成されるグラフの形式で表すことができます。 テストでのグラフのカバレッジは、さまざまなカバレッジ基準を使用してテストを設計し、エラーを特定できるという点で便利です。 ブラックボックスのテストに関しては、状態と遷移、エンティティ状態グラフなどを操作する必要がある場合、ここのグラフカバレッジも非常に重要になります。 グラフが非常に複雑な場合、異なるカバレッジ基準により、テストスイートの妥当性を評価できます。
最初の部分では、定義、頂点のカバレッジ、エッジ、パス、循環的複雑度。
定義：メインパス
- 単純なパスとは、最初と最後（一致する可能性がある）を除き、頂点が複数回表示されないパスです。 単純なパスには内部ループはありません。 最大長の単純なパスは、メインパスと呼ばれます。
- メインパスは、他の単純なパスのセグメントではない単純なパスです。 わかりやすくするために言い換えると、メインパスには内部ループがなく（頂点は一意です）、同様のパスの中で最も長いパスです。 長くすることができる場合、それは別の単純なパスのセグメントです。つまり、メインパスではありません。 （これは、気づくとすぐに非常に単純な概念であることがわかります。）
- たとえば、パス[1、2、3、4、5、6、1]を考えます（この記事のグラフには関係ありません）。 これは、最初と最後を除いて、すべてのピークが一意であるため、簡単な方法です。 このパスは他のセグメントのセグメントではないという仮定に基づいて、メインパスにもなります。 一方、[1、2、3、4、4]は、[1、2、3、4、5、6、1]、[1、2、3、4]があることがわかっているため、メインのパスにすることはできません。 4]-間違いなく彼のセグメント。 そして、メインではありません。
- 閉じたパスは、同じ頂点で開始および終了する長さがゼロ以外のメインパスです。 [1、2、3、4、5、6、1]-基本的で閉じたシンプルなパス。
プライマリパスコーティング（EPP）
テストカバレッジ要件には、列Gのすべてのメインパスが含まれています。
グラフ内の単純なパスは、メインのパスよりもはるかに小さくなっています。 したがって、グラフ内のすべての主要なパスをカバーすることは、検討する価値のあるパスの総数を減らす良い方法です。 テストパスの数は、特定のパスをカバーする場合のように、テスターの主観的な判断に依存することなく削減され、パスを完全にカバーする場合のように、要件は計算に時間がかかりません。
アプローチは簡単です。 メインパスのセットを定義し、それぞれを実装するテストケースを準備します。
メインパスのカバレッジには、ピーク、リブ、およびリブのペアワイズカバレッジが含まれます。 いくつかの情報源によると、EPPには一対のリブは含まれていません。 引数は次のとおりです。頂点nにエッジがあり、そこからエッジが入る場合、エッジをペアワイズカバーするための次の要件が作成されます。[n、n、m]、 mはnのレシーバです。 [n、n、m]は明らかにメインパスではないため、メインパスをカバーすることはこのパスを含むことができません。つまり、メインパスをカバーすることは、エッジをペアワイズカバーすることを含みません。 ペアワイズカバーエッジのテスト要件には[n、n、m]が含まれていませんが、[n、n]が含まれているため、このロジックは完全に正しいわけではありません。
要件= {
[1、2、6]、
[1、2、3、4、6]、
[1、2、3、4、5]、
[2、3、4、5、2]、
[3、4、5、2、3]、
[4、5、2、3、4]、
[5、2、3、4、5]、
}
パス（T）= {
[1、2、6]、
[1、2、3、4、6]、
[1、2、3、4、5、2、3、4、5、2、6]
}
最後のテストパスがわずかに長い理由は、すべての要件をカバーするために、1回ではなく2回サイクルを実行する必要があるためです。
主な方法を探す
メインパスをカバーするには、最初にすべてを見つける必要があります。 これを行う最も簡単な方法は、グラフの最長パスをリストすることから始めることです。
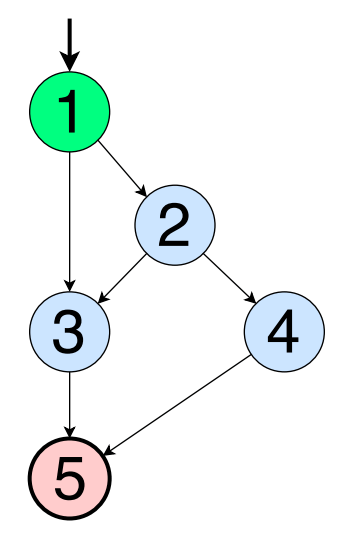
上記の例のグラフを使用して、最も長いパスをリストすることから始めます。
[1、2、3、5]
[1、2、4、5]
定義上、メインパスは別のパスのセグメントではない単純なパスです。 一般に、グラフのメインパスは最長よりも短くなっています。 これらのパスはループ内に「隠れ」ています（詳細は下）が、上のグラフの場合、最後のメインパスは直接[1、3、5]です。 他のすべてのパス、たとえば[2、3、5]、すでにリストされているパスのセグメント。 基本的なパスの完全なセットは次のとおりです。
[1、2、3、5]
[1、2、4、5]
[1、3、5]
上記のように、メインパスはループ内で「非表示」になります。 ループ内にx個の頂点がある場合、 x個のプライマリパスが追加されます。
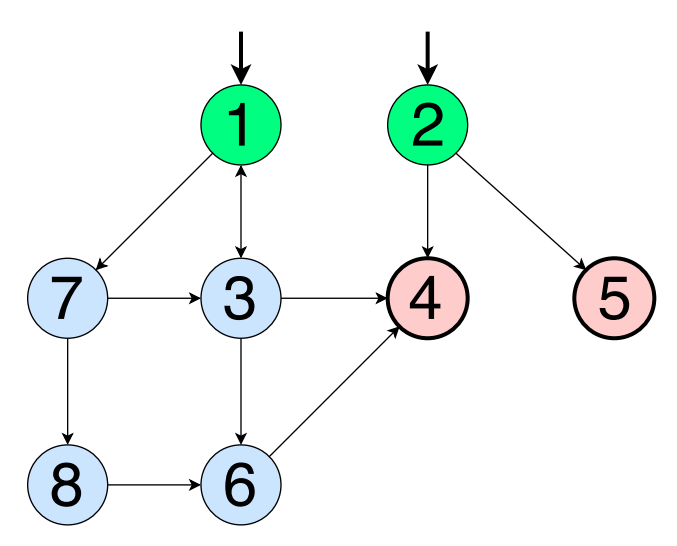
前に使用した方法を使用すると、次の主な方法が得られます。
[1、2、3、4、6]
[1、2、6]
[1、2、3、4、5]
頂点2から開始して、ループを1回回り、頂点2に戻ります。これが最初のメインパスです。 頂点3から開始して、再びサイクルを回って戻ります。 したがって、2番目の主要な方法が判明します。 頂点4と5について同じことを繰り返すと、4つの追加のメインパスが得られます。 それらを上記のリストと比較すると、これらは完全に新しいメインパスであることがわかります（つまり、上記のいずれのセグメントでもありません）。 同じピークで開始および終了する主なパスは、クローズと呼ばれます。
[2、3、4、5、2]
[3、4、5、2、3]
[4、5、2、3、4]
[5、2、3、4、5]
メインパスと閉じたパスに精通したので、さらにいくつかの基準について説明します。
単純な閉路カバー
PRSPの要件には、閉じたパスを開始および終了するGの到達可能な頂点の少なくとも1つの閉じたパスが含まれます。
簡単に言えば、これは、上記のすべての閉じたパスの中で、サイクルごとに1つ取るということです。 グラフに別のサイクルがある場合、PRZP条件を満たすために、このサイクルの頂点をカバーする閉じたパスを取る必要があります。
例として、前のセクションのグラフをもう一度考えてみましょう。
要件= {[2、3、4、5、2]}
パス（T）= {[1、2、3、4、5、2、6]}
PRZPは、すべての閉じたパスのすべての頂点がカバーされている場合、各サイクルに1つの閉じたパスのみを必要とします。
閉じたパスの完全なカバレッジ
PrPZPに似ていますが、すべての閉じたパスが含まれます。
要件には、グラフ内の到達可能な各頂点のすべての閉じたパスが含まれます。
要件= {
[2、3、4、5、2]、
[3、4、5、2、3]、
[4、5、2、3、4]、
[5、2、3、4、5]
}
パス（T）= {
[1、2、3、4、5、2、3、4、5、2、6]
}
LARPの要求に応じて、すべての閉じたパスをカバレッジに含めました。 まだ気付いていない場合、PPZPとPrZPZには、閉じたパスにないグラフの頂点とエッジをスキップするという奇妙な特性があることに注意することが重要です。 これは、エッジのペアワイズカバー、エッジまたは頂点のカバーが含まれないことを意味します。 以下の包含図をご覧ください。
