Clever Geek Handbook

数学の簡単な問題の例としてのスペクトル法

この記事では、計算流体力学、地球物理学、気候学、その他多くの分野で使用される数学の方程式の数値解法の擬似スペクトル法について説明します。



画像








ロッドに沿った熱伝播の一次元問題



まず、ロッド内の熱伝播の単純な1次元の問題を考えます。 ロッド上の特定の初期温度分布での熱の分布を表す方程式：



画像



画像



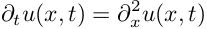
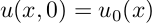
このような方程式は、変数の分離方法、たとえばここで分析的に解かれますが 、これを数値的に行う方法に興味があります。 まず、xに対する2次空間微分の計算方法を決定する必要があります。 これは、たとえば次のような異なる方法で最も簡単に実行できます。



画像



しかし、我々はそうしません。 温度分布は座標と時間の関数であり、この関数は各時点でフーリエ級数の合計として表すことができ、n番目の項で数値的に切り捨てられます。



画像



ここで、u ^ "キャップ付き"はフーリエ級数の展開係数です。 熱伝達方程式のシリーズに式を代入します。



画像



画像



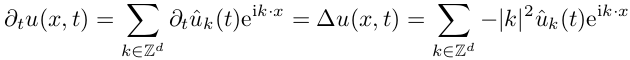
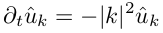
フーリエ係数の方程式を取得します。この方程式では、座標に関する微分はありません！ これは偏微分ではなく、通常の微分方程式であり、単純な差分法で解くことができます。 既に簡単になりましたが、今では展開係数を見つけることが残っており、 高速フーリエ変換 （以降FFT）が非常に役立ちます。



ここでのロジックは次のとおりです。



1）最初の時点で、ロッド全体の温度分布を記述する座標関数が与えられます。

2）ロッドをnポイントのグリッドに分割します。

3）FFTアルゴリズムを使用して複素フーリエ係数を見つけ、F（u）として操作を示します。

4）得られた係数に-| k |を掛けます 2、2 次導関数のフーリエ変換を取得します。 同様に、高次数pの導関数のフーリエ変換を取得できます 。 （ik） pを乗算するだけです。

5）逆フーリエ変換F -1 （u）を行い、IFFTアルゴリズムを使用して、グリッド上のポイントで2次導関数の値を取得します。

6）私たちはタイムステップを踏む、すでに通常の違い、明示的または暗黙的、スキーム;

7）繰り返します。



次に、Matlab / Octaveのプログラムでどのように機能するかを見てみましょう。 初期温度分布として、滑らかな関数u0 = 2 + sin（x）+ sin（2x）を使用し、ロッド2πを50ポイントに分割します。時間ステップh = 0.1で、境界条件は周期的です（リング）。



一次元熱伝達方程式のコード 
clear all; n = 50; % number of points dx = 2*pi/n; % space step x = 0:dx:2*pi-dx; % grid h = 0.1; % temporal step times = 10; % number of iterations in time k = fftshift(-n/2:1:n/2-1); % wave numbers k2 = k.*k; u0 = 2 + sin(x) + sin(2*x); % initial conditions u = zeros(times,n); % stores results u(1,:) = u0; uf = fft(u0); % Fourier coefficients of initial function for i=2:times uf = uf.*(1-h*k2); % next time step in Fourier space u(i,:) = real(ifft(uf)); % IFFT to physical space end [X,T] = meshgrid(x,0:h:times*hh); waterfall(X,T,u)




出力d = fft（u）で得られた展開係数は順番ではなく、シフトされているという事実に関連するMatlabのFFTアルゴリズムの機能に注目する価値があります。前半は後半の代わりに、逆も同様です。 最初に、0からn / 2-1の数値を持つ係数があり、次に-n / 2から-1の数値を持つ係数があります。 これに問題がありました...



画像



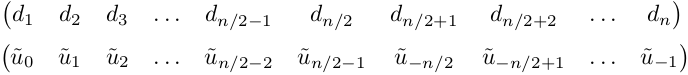
結果の解は、各時間tのxに沿った温度分布線の「滝」の形でグラフに表示されます。 解が数値的不安定性の強い振動を経験することがわかります 。これはクーラント基準の失敗によるものです。 タイムステップを減らすか、たとえばCrank-Nicholsonなどのより高度な暗黙的なスキームを適用することにより、不安定性を取り除くことができます。



画像








二次元拡散方程式



画像



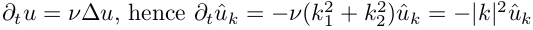
初期条件：u0 = 1 + sin（2X）+ cos（2Y）。ここで、uは2次元配列u（i、j）です。 暗黙の時間積分スキームを使用します（つまり、m番目のm + 1ステップを表します）。



画像



画像



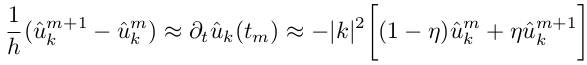
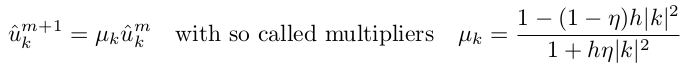
このような暗黙のスキームは、η> 0.5で発散しないことが証明できます;η= 1を使用します。 したがって、u m + 1の各新しい値は、u mに係数μkを乗算することによって取得されます。これは、時間ステップと波数kに依存します。 μkは、ステップごとにカウントする必要のない定数です！



二次元拡散方程式のコード 
 clear all; eta = 1; n = 32; % number of points dx = 2*pi/n; % space step x = 0:dx:2*pi-dx; y = x; [X, Y] = meshgrid(x,y); h = 0.01; % temporal step times = 30; % number of iterations in time k1 = meshgrid(fftshift(-n/2:1:n/2-1),ones(n,1)); k2 = k1'; ks = k1.*k1 + k2.*k2; mu = (1-(1-eta)*ks^2*h)./(1+eta*ks.^2*h); % stores multipliers u0 = 1 + sin(2*X) + sin(2*Y); % initial temperature u = zeros(times,n,n); % stores results umin=min(min(u0)); umax=max(max(u0)); u(1,:,:) = u0; uf = fft2(u0); for i=2:times uf = mu.*uf; % time step u(i,:,:) = real(ifft2(uf)); end createGif('diffusion2d.gif',X,Y,u,times,1,[0 2*pi 0 2*pi umin umax]);




GIFを保存する 
 function createGif(name,X,Y,u,times,every,ax) % creates gif movie form 3D array % save results to gif file gifka = name; clf; pic = surf(X,Y,squeeze(u(1,:,:))),axis(ax); for i=1:every:times set(pic,'zdata',squeeze(u(i,:,:))), drawnow; M(i) = getframe; frame = getframe; im = frame2im(frame); [imind,cm] = rgb2ind(im,256); if i == 1; imwrite(imind,cm,gifka,'gif','Loopcount',inf); else imwrite(imind,cm,gifka,'gif','WriteMode','append','DelayTime',.1); end end end




画像








二次元波動方程式



画像

波動方程式には2次微分があり、したがってタスクは2つの通常ディファーのシステムに削減され、1つの変数はu、2番目はu t 、コードの時間スキームは最も単純な明示的なものを使用するため、精度は小さく、時間ステップは非常に小さくなりますが、コードは比較的単純に見えます。 ただし、これはメソッドの操作性を実証するには十分です。



二次元波動方程式のコード 
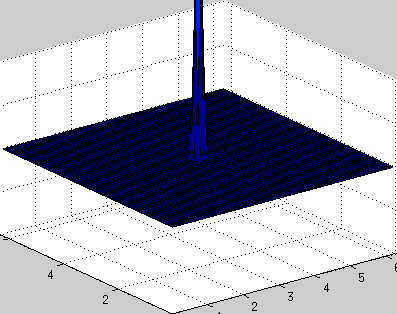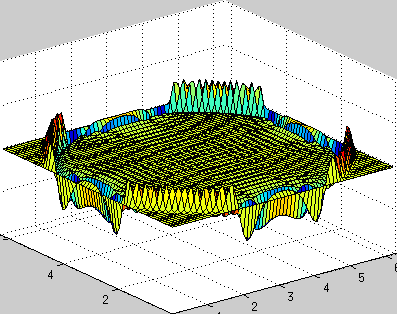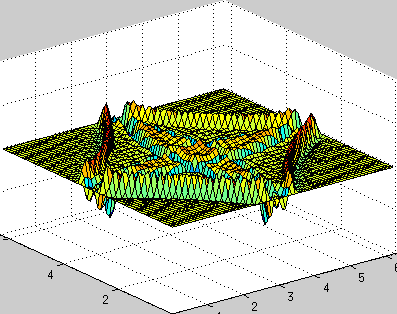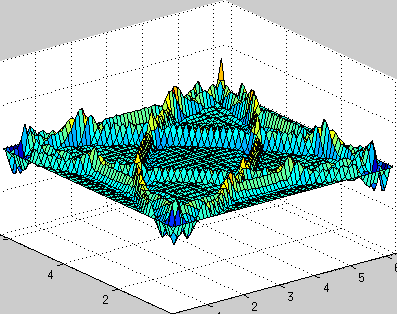
 clear all; a = 1; % speed of wave propagation n = 64; % number of points dx = 2*pi/n; % space step x = 0:dx:2*pi-dx; y = x; [X, Y] = meshgrid(x,y); h = 0.01; % temporal step times = 1000; % number of iterations in time % explanation of this part is here www.staff.uni-oldenburg.de/hannes.uecker/pre/030-mcs-hu.pdf k1 = meshgrid(fftshift(-n/2:1:n/2-1),ones(n,1)); k2 = k1'; ks = k1.*k1 + k2.*k2; u0 = exp(-100*((X-pi).^2 + (Y-pi).^2)); % profile of initial velocity u ut0 = zeros(n,n); % profile of initial acceleration ut u = zeros(times,n,n); % stores velocity profile for every time steps u(1,:,:) = u0; uf = fft2(u0); uft = fft2(ut0); for i=2:times uft_new = uft - a*h*ks.*uf; uf = uf + 0.5*h*(uft+uft_new); uft = uft_new; % == fixed boundary conditions % u0 = real(ifft2(uf)); % u0(1,:) = 0; u0(end,:) = 0; % u0(:,1) = 0; u0(:,end) = 0; % uf = fft2(u0); % == fixed boundary conditions u(i,:,:) = real(ifft2(uf)); end createGif('wave2d_periodic_bc.gif',X,Y,u,times,10,[0 2*pi 0 2*pi -.2 .2]);




周期的境界条件：



画像








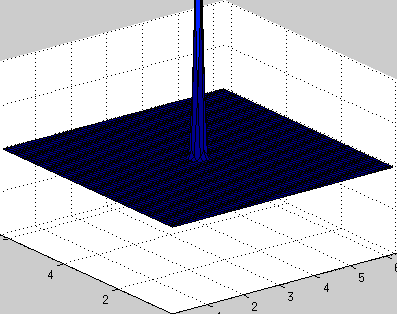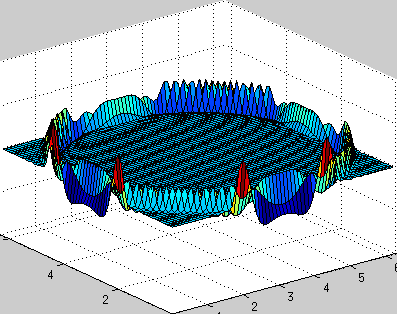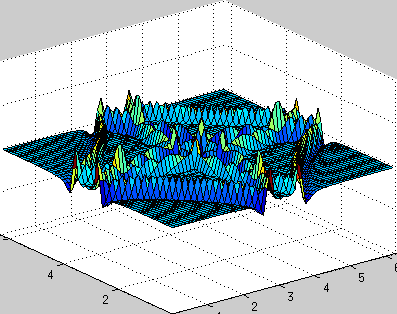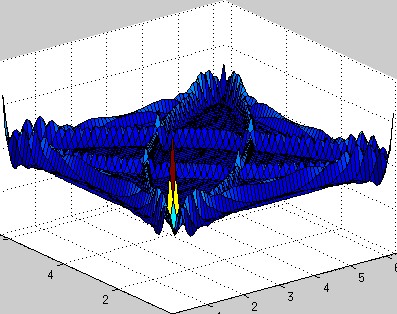
固定境界条件（エッジで0、境界からの波の反射）：



画像






結論



この記事では、数学の単純な問題に対するスペクトル法の使用例をいくつか示します。 スペクトル法の主な本質は、元の偏微分方程式を、何らかの方法で目的の関数の展開係数の通常のディファーで置き換えることです。 ジオメトリが必要な場合、基底は正弦余弦、複素指数、直交多項式になります-円筒関数または球面関数。 各時点で検出された係数により、目的のソリューションを復元できます。FFTアルゴリズムを使用すると、これをすばやく行うことができます。



この方法の利点は次のとおりです。



  1. 「良い」機能のための良い精度。 グリッドポイントnの数が増えると、有限差分法の誤差はO（N -m ）として減少します（mは、メソッドの次数と関数の滑らかさに依存する特定の定数です）。スペクトル法では、精度は指数O（c N ）になります。ここで、0 <c <1。
  2. 比較的使いやすい、特に比較のために高次の導関数を見つける場合、有限差分法ではかなり複雑な式を使用する必要があります。 有効なFFTアルゴリズムの適用により、O（N log（N））の複雑度が得られます。これは、十分に大きな問題に受け入れられる
  3. スペクトル法はメモリに関して効果的であるため、地球物理学、気候モデリング、気象学で広く使用されています。


欠点も利用できます：



  1. ギブス現象 、非常に悪い現象、領域の端の精度に強く影響する
  2. 差分法よりも自由度の高いコンピューティングリソースを要求する
  3. 非標準のジオメトリ、および周期的以外の境界条件の問題にはあまり適用できません。


私の最初の記事が誰かに役立つことを願っています。少なくともこれは、数値計算法のこのセクションを勉強している人にとっては可能な出発点です。 コード 、デザイン、ヒントに関する重要なコメントを楽しみにしています ！



使用したソース



  1. Hannes Ueckerによるコード例付きの素晴らしいレビュー。この記事で使用したもののいくつか
  2. Lloyd N. Trefethenによる小さくて素晴らしい本、MATLABのスペクトル法
  3. ジョン・P・ボイドによる基本書「チェビシェフとフーリエスペクトル法」


More articles:


All Articles